Bangun Ruang

Bangun ruang merupakan suatu bangun tiga dimensi yang memiliki ruang/ volume/ isi dan juga sisi-sisi yang membatasinya.

Secara garis besar, bangun ruang bisa kita kategorikan menjadi dua kelompok, antara lain: bangun ruang sisi datar dan bangun ruang sisi lengkung.

Yang termasuk dalam bangun ruang sisi datar yaitu kubus, balok, prisma, dan limas. Sementara untuk bangun ruang sisi lengkung terdiri atas kerucut, tabung, dan bola.

Macam-macam Bangun Ruang

Berikut ini akan kami berikan macam-macam dari bangun ruang, mulai dari bangun ruang sisi datar yang meliputi kubus, balok, prisma, dan limas. Hingga bangun ruang sisi lengkung yang meliputi kerucut, tabung, dan bola.

1. Kubus

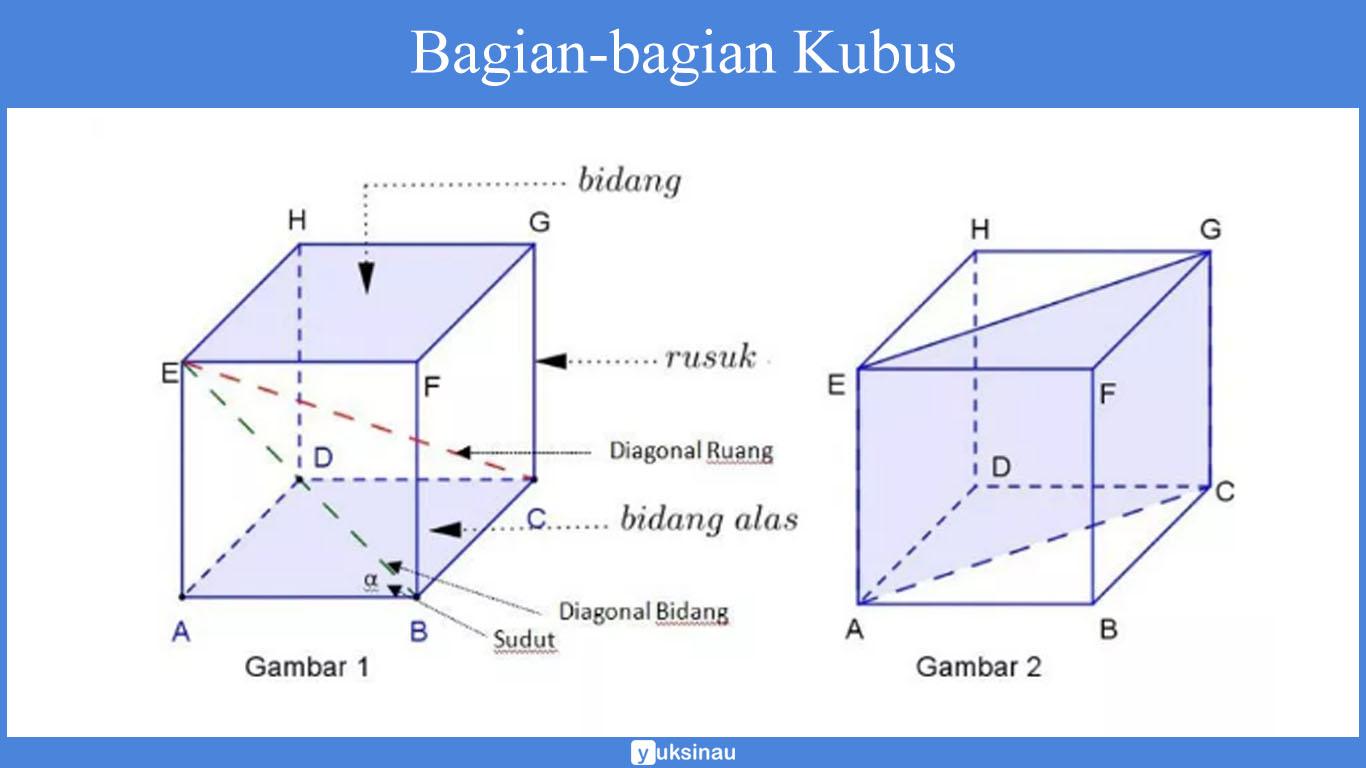
Kubus merupakan suatu bangun ruang tiga dimensi yang dibatasi oleh enam sisi serupa yang berwujud bujur sangkar.

Kubus juga dikenal dengan nama lain yaitu bidang enam beraturan. Kubus sebetulnya adalah bentuk khusus dari prisma segiempat, sebab tingginya sama dengan sisi alas.

Sifat bangun Kubus

1. Memiliki 6 sisi berbentuk persegi yang memiliki ukuran sama luas
2. Memiliki 12 rusuk yang memiliki ukuran sama panjang
3. Memiliki 8 titik sudut
4. Memiliki 4 buah diagonal ruang
5. Memiliki 12 buah bidang diagonal

Rumus Pada Kubus

Volume: V= s x s x s = s³
Luas permukaan: 6 s x s = 6 s²
Panjang diagonal bidang: s√2
Panjang diagonal ruang: s√3
Luas bidang diagonal: s²√2

Keterangan:

L= Luas permukaan kubus (cm²)
V= Volume kubus (cm³)
S= Panjang rusuk kubus (cm)

2. Balok

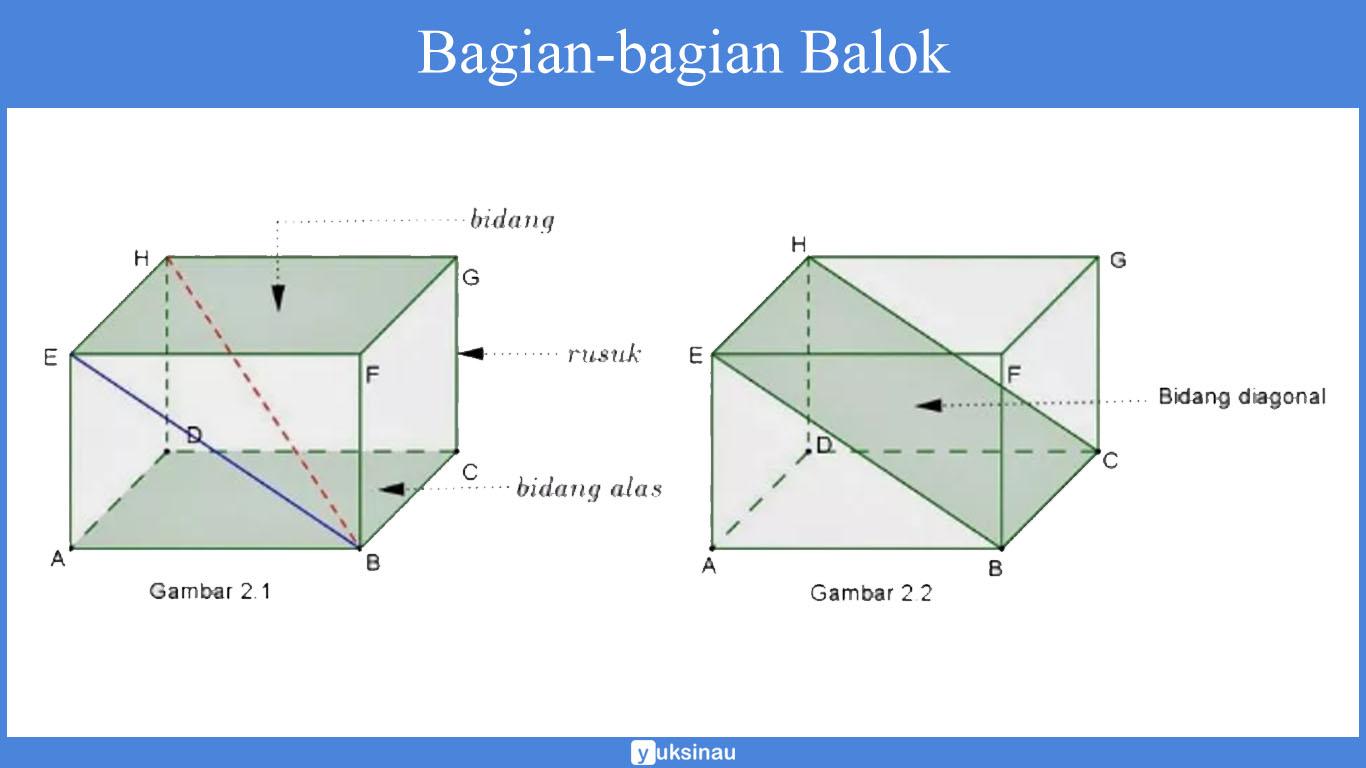
Balok adalah suatu bangun ruang yang mempunyai tiga pasang sisi segi empat. Di mana pada masing-masing sisinya yang berhadapan mempunyai bentuk serta ukuran yang sama.

Berbeda halnya dengan kubus di mana seluruh sisinya kongruen berbentuk persegi, dan pada balok hanya sisi yang berhadapan yang sama besar.

Serta tidak seluruhnya berbentuk persegi, kebanyakan berbentuk persegi panjang.

Sifat Balok

1. Sedikitnya sebuah balok mempunyai dua pasang sisi yang berbentuk persegi panjang.
2. Rusuk-rusuk yang sejajar memiliki ukuran yang sama panjang:
   AB = CD = EF = GH, dan AE = BF = CG = DH.
3. Pada masing-masing diagonal bidang pada sisi yang berhadapan berukuran sama panjang, yakni:
   ABCD dengan EFGH, ABFE dengan DCGH, dan BCFG dengan ADHE yang mempunyai ukuran sama panjang.
4. Masing-masing diagonal ruang pada balok mempunyai ukuran sama panjang.
5. Masing-masing bidang diagonalnya berbentuk persegi panjang.

Rumus pada Balok:

Volume: p.l.t
Luas Permukaan: 2 (pl + pt + lt)
Panjang Diagonal Bidang: √(p²+l²) atau juga bisa √(p²+t²) atau √(l²+t²)
Panjang Diagonal Ruang: √(p²+l²+t²)

Keterangan:

p : panjang
l : lebar
t : tinggi

3. Limas

Limas merupakan suatu bangun ruang tiga dimensi yang dibatasi oleh alas berbentuk segi-n (dapat berupa segi tiga, segi empat, segi lima, dll) serta bidang sisi tegak berbentuk segitiga yang berpotongan di satu titik puncak.

Terdapat banyak jenis limas yang dikategorikan dengan dilandasi bentuk alasnya. Antara lain: limas segitiga, limas segi empat, limas segi lima, dan yang lainnya.

Limas dengan mempunyai alas berbentuk lingkaran disebut sebagai kerucut. Sementara untuk limas dengan alas yang berupa persegi disebut sebagai piramida.

Sifat limas:

Bangun limas juga memiliki beberapa sifat atau ciri, diantaranya ialah sebagai berikut:

• Memiliki 5 sisi yakni: 1 sisi berbentuk segiempat yang berupa alas serta 4 sisi lainnya seluruhnya berbentuk segitiga dan merupakan sisi tegak.
• Memiliki 8  buah rusuk.
• Memiliki 5 titik sudut, antara lain: 4 sudut terletak di bagian alas serta 1 sudut terletak di bagian atas yang merupakan titik puncak.

Volume Limas = 1/3 Luas Alas x Tinggi
Luas Permukaan = Jumlah Luas Alas + Jumlah Luas sisi tegak

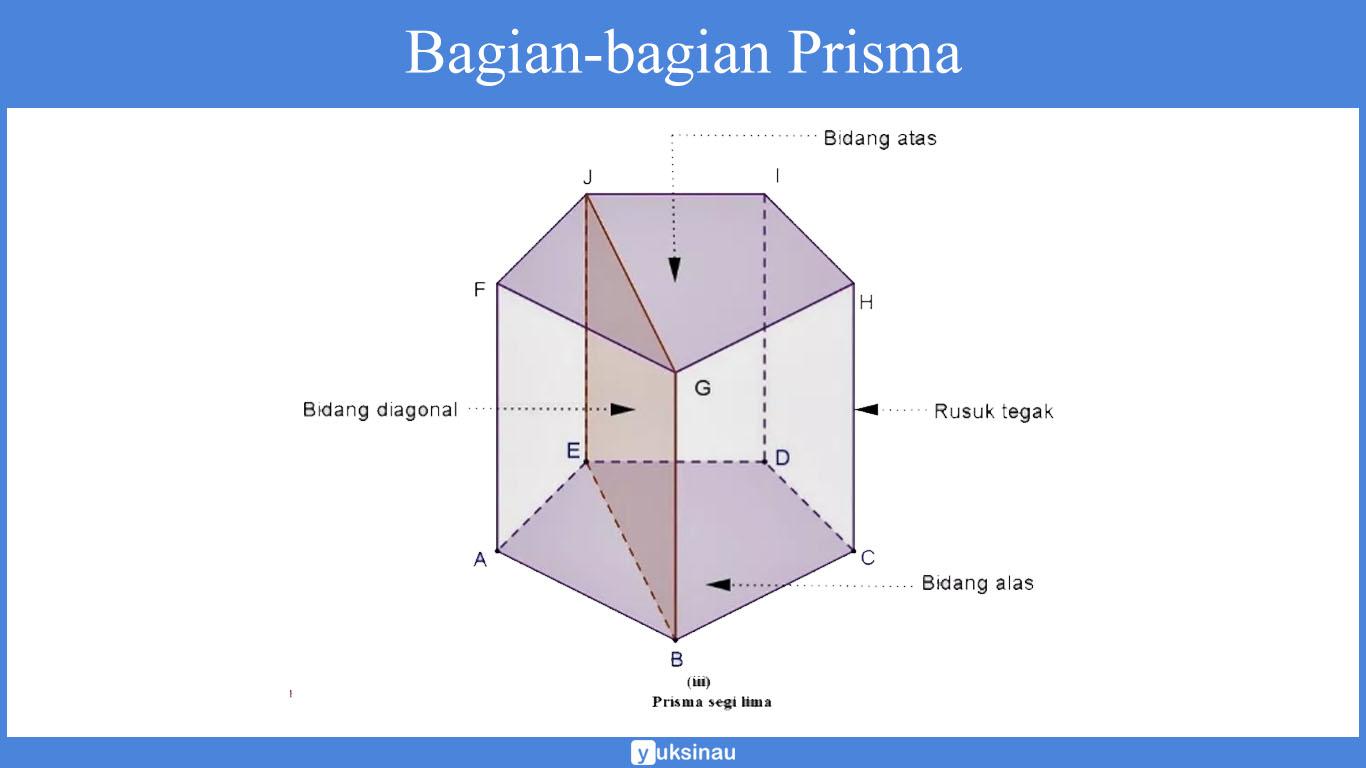
4. Prisma

Prisma merupakan suatu bangun ruang tiga dimensi di mana alas dan juga tutupnya kongruen serta sejajar berbentuk segi-n.

Sisi-sisi tegak dalam prisma memiliki beberapa bentuk, antara lain: persegi, persegi panjang, atau jajargenjang.

Dilihat dari tegak rusuknya, prisma terbagi menjadi dua macam, yaitu: prisma tegak dan prisma miring.

Prisma tegak merupakan prima di mana rusuk-rusuknya tegak lurus dengan alas dan juga tutupnya. Sementara untuk prisma miring merupakan prisma di mana rusuk-rusuk tegaknya tidak tegak lurus pada alas dan juga tutupnya.

Apabila kita lihat dari bentuk alasnya, prisma terbagi lagi menjadi beberapa macam, yaitu: prisma segitiga, prisma segi empat, prisma segi lima, dan lain sebagainya.

Prisma yang alas dan juga tutupnya berbentuk persegi disebut sebagai balok dan kubus. Sementara untuk prisma yang memiliki alas dan tutupnya berbentuk lingkaran disebut sebagai tabung.

Sifat Prisma

Bangun limas juga mempunyai beberapa sifat atau ciri, diantaranya ialah sebagai berikut:

• Memiliki bidang alas dan juga bidang atas yang berupa segitiga kongruen (2 alas tersebut juga merupakan sisi prisma segitiga).
• Memiliki 5 sisi (2 sisi yang berupa alas atas serta bawah, 3 sisi lainnya adalah sisi tegak yang seluruhnya berbentuk segitiga).
• Memiliki 9 rusuk.
• Memiliki 6 titik sudut.

Rumus Pada Prisma

• Rumus menghitung luas:
  Luas = (2 x luas alas) + (luas seluruh bidang tegak)
• Rumus menghitung keliling:
  K = 3s (s + s + s)
• Rumus menghitung Volume:
  Volume Prisma = Luas segitiga x tinggi
  atau juga bisa
  Volume Prisma = 1/2 x a.s x t.s x t

5. Bola

Bola merupakan salah satu bangun ruang sisi lengkung yang dibatasi oleh satu bidang lengkung. Atau juga bisa didefinisikan sebagai sebuah bangun ruang berbentuk setengah lingkaran yang diputar mengelilingi garis tengahnya.

Sifat Bola

1. Bola memiliki 1 sisi serta 1 titik pusat.
2. Bola tidak memiliki rusuk.
3. Bola tidak memiliki titik sudut
4. Tidak memiliki bidang diagonal
5. Tidak memiliki diagonal bidang
6. Sisi bola disebut sebagai dinding bola.
7. Jarak dinding ke titik pusat bola disebut sebagai jari-jari.
8. Jarak dinding ke dinding serta melewati titik pusat disebut sebagai diameter.

Rumus pada Bola

Rumus untuk menghitung volume bola yakni:
4/3 x π x r³

Rumus untuk menghitung luas bola yakni:
4 x π x r²

Keterangan:

V : Volume bola (cm³)
L : Luas permukaan bola (cm²)
R : Jari – jari bola (cm)
π : 22/7 atau 3,14

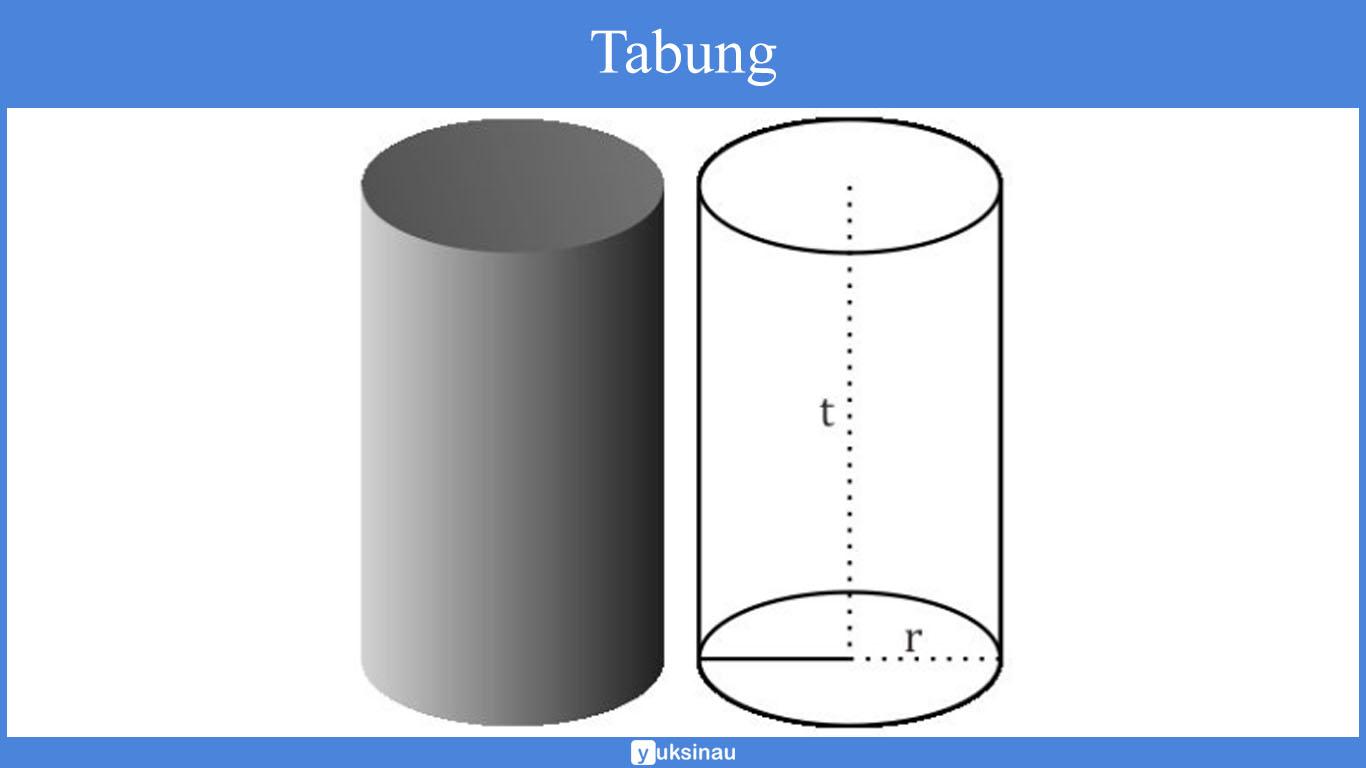
6. Tabung

Bangun tabung merupakan suatu bangun ruang tiga dimensi yang mempunyai tutup dan alas yang berbentuk lsebuah ingkaran dengan memiliki ukuran yang sama dan diselimuti oleh persegi panjang.

Sifat Tabung

1. Tabung memiliki 3 buah sisi, 1 persegi panjang, 2 lingkaran.
2. Tidak memiliki rusuk.
3. Tidak memiliki titik sudut.
4. Tidak memiliki bidang diagonal.
5. Tidak memiliki diagonal bidang.
6. tabung memiliki sisi alas serta sisi atas berhadapan yang kongruen.
7. Tinggi tabung merupakan jarak titik pusat bidang lingkaran alas dengan titik pusat lingkaran atas.
8. Bidang tegak tabung berwujud lengkungan yang disebut sebagai selimut tabung.
9. Jaring-jaring tabung berwujud 2 buah lingkaran serta 1 persegi panjang.

Rumus pada Tabung

• Rumus untuk menghitung luas alas:
  luas lingkaran=π x r²
• Rumus untuk menghitung volume pada tabung:
  π x r² x t
• Rumus untuk menghitung keliling alas pada tabung:
  2 x π x r
• Rumus untuk menghitung luas pada selimut tabung:
  2 x π x r x t
• Rumus untuk menghitung luas pada permukaan tabung:
  2 x luas alas+luas selimut tabung
• Rumus kerucut + tabung:
  • volume = ( π.r².t )+( 1/3.π.r².t )
  • luas = (π.r²)+(2.π.r.t)+(π.r.s)

• Rumus tabung + 1/2 bola:
  • Rumus untuk menghitung Volume = π.r².t+2/3. π.r³
  • Rumus untuk menghitung Luas = (π.r²)+(2.π.r.t)+(½.4.n.r²) = (3.π.r²)+(2. π .r.t)

• Rumus tabung+bola:
  • Rumus untuk menghitung Volume= (π.r².t)+(4/3. π.r³)
  • Rumus untuk menghitung Luas= (2. π.r²)+(4. π.r²) = π.r²

Keterangan:

• V = Volume tabung(cm³)
• π = 22/7 atau 3,14
• r = Jari – jari /setengah diameter (cm)
• t = Tinggi (cm)

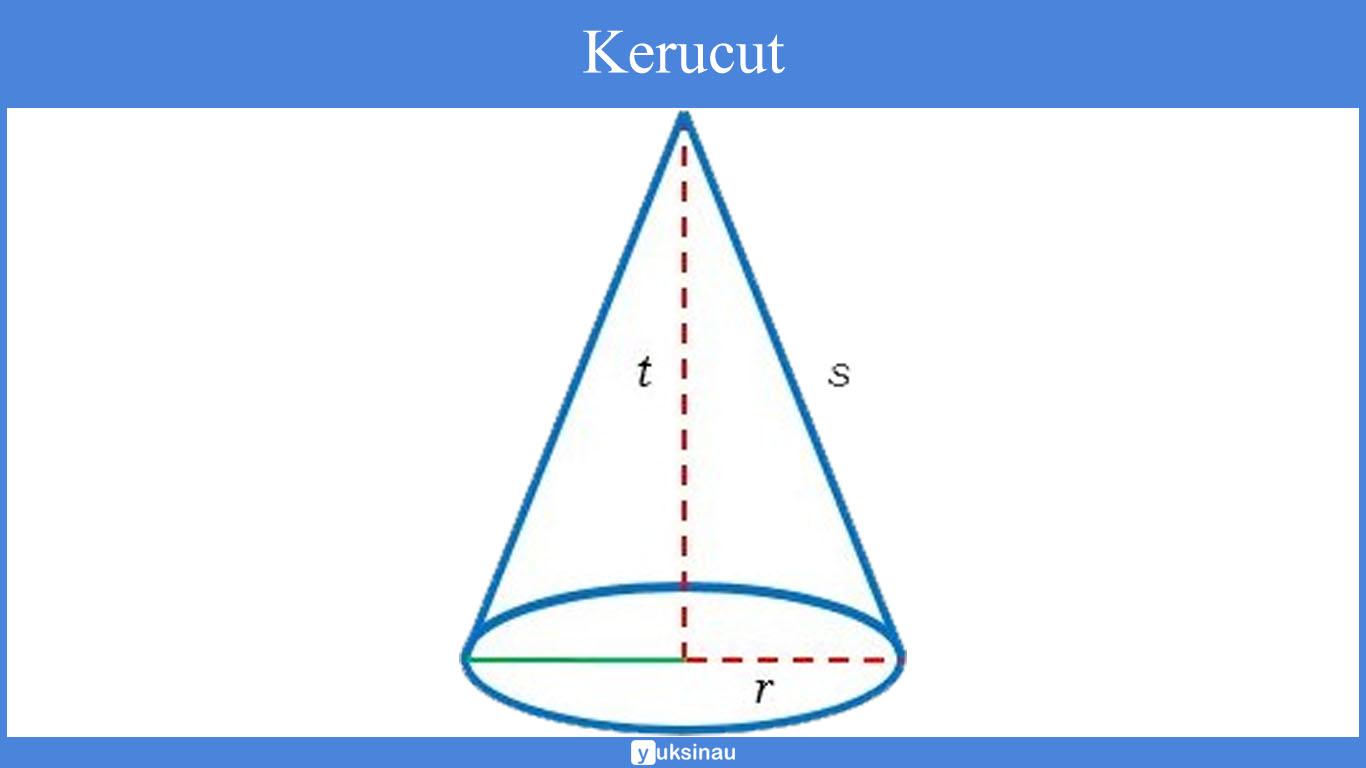
7. Kerucut

Kerucut merupakan salah satu bangun ruang yang memiliki sebuah alas yang berbentuk lingkaran dengan selimut yang mempunyai irisan dari lingkaran.

Sifat Kerucut

Terdapat beberapa sifat pada bangun ruang kerucut, antara lain ialah sebagai berikut:

1. Kerucut memiliki 2 sisi.
2. Kerucut tidak  memiliki rusuk.
3. Kerucut memiliki 1 titik sudut.
4. Jaring-jaring kerucut terdiri atas lingkaran serta segitiga.
5. Tidak memiliki bidang diagonal
6. Tidak memiliki diagonal bidang

Rumus pada bangun ruang kerucut

Rumus untuk menghitung volume:
1/3 x π x r x r x t

Rumus untuk menghitung luas:
luas alas+luas selimut

Keterangan:

• r = jari – jari (cm)
• T = tinggi(cm)
• π = 22/7 atau 3,14

Contoh Soal dan Pembahasan Bangun Ruang

Untuk menambah pemahaman pada uraian di atas, maka akan kami berika beberapa contoh soal sekaligus pembahasannya. Simak baik-baik ya.

Soal 1. Bangun Kubus

Suatu kubus mempunyai panjang rusuk 6 cm. Rusuk itu kemudian akan diperpanjang sebesar k kali panjang rusuk semula, sehingga volumenya berubah menjadi 1.728 cm3 .

Hitunglah nilai k dari panjang rusuk tersebut!

Jawab:

Skubus semula = 6 cm

Vkubus akhir= S x S x S
= S3

S = ∛1.728
= 12 cm

Nilai k = 12 cm / 6 cm
= 2

Sehingga, Nilai k nya yaitu 2 kali.

Soal 2. Bangun Balok

Rusuk-rusuk balok bertemu pada suatu balok sebuah pojok balok berbanding 4:4:1 apabila volume balok 432 liter, luas permukaan balok yaitu ….

Jawab: 

Tahapan:

• Mencari nilai rusuk balok dengan perbandingan dan volume
• Mencari luas permukaan balok

Total perbandingan dari volume = 4 x 4 x 1 = 16

R1 = 4/16 x 432
= 108 dm

R2 = 4/16 x 432
= 108 dm

R3 = 1/16 x 432
= 27 dm

R₁ : R₂ : R₃ = 108 : 108 : 27 = 12 : 12 : 3

Luas Permukaan
= 2 Luas alas + (Keliling alas x tinggi)
= 2 (12 x 12) + (4 x 12 x 3) (Sebab alas berbentuk persegi)
= 288 + 144
= 432 dm₂

Sehingga, luas permukaannya yaitu sama dengan volume yakni 432 dm.

Soal 3. Bangun Prisma

las dari suatu prisma berbentuk segitiga siku-siku dengan memiliki panjang sisi miring 35 cm serta panjang salah satu sisi siku-sikunya 21 cm.

Jika tinggi prisma 20 cm, maka luas sisi prismanya yaitu …

Jawab:

Tahapan:

• Mencari sisi siku-siku alas

Sisi tegak = A
A2 = C2 – B2
= 352 – 212
= 1225 – 441
= 784
A   = 28 cm

Luas sisi Prisma = 2 x Luas alas + Keliling alas x tinggi
= 2 x (1/2 x A x B) + (A + B + C) x tinggi
= (2 x ½ x 21 x 28) + (28 + 21 + 35) x 20
= 588 + (84 x 20)
= 2268 cm2

Soal 4. Bangun Limas

Diketahui sebuah limas segiempat mempunyai panjang 20 cm serta lebar 15 cm. Tinggi segitiga selimut diketahui sepanjang 10 cm.

Hitunglah luas permukaan limas!

Jawab:

Rumus Luas Permukaan = ( p x l ) + (2 x 1/2 x p x t.selimut) + (2 x 1/2 x l x t.selimut)
= ( 20 x 15 ) + (2 x 1/2 x 20 x 10) + ( 2 x 1/2 x 15 x 10)
= 300 + 200 +150
L = 650 cm2

Sehingga, luas permukaan limas tersebut yaitu 650 cm2

Soal 5. Kerucut

Tentukan volume kerucut terpancung jika diameter alasnya 10 dm, diameter sisi atas 4 dm, dan tinggi 4 dm! Jari-jari alas = 5dm , Jari-jari atas = 2dm

Gunakan rumus: V = phi×t (R.alas2 + R.alas × R.atas + R.atas2 )

Jawab:

= 3,14×4dm (5dm×5dm + 5dm×2dm + 2dm×2dm)
= 12,56dm (25dm2 + 10dm2 + 4dm2)
= 12,56dm (39dm2)
= 12,56dm × 39dm2
= 489,84dm3

Soal 6. Bola

Sebuah balon udara berwujud bola serta terbuat dari bahan elastis. Hitunglah berapa luas bahan yang dibutuhkan untuk membuat balon udara tersebut apabila diameternya 28 m dengan π=22/7!

Jawab:

Diketahui:

• d = 28 → r = 14

Ditanyakan:

• Luas ?

Penyelesaian:

L = 4πr²

L = 4×22/7×14×14

L =  2.464 m²

Sehingga, luas bahan yang diperlukan yakni 2.464 m²

Soal 7. Tabung

Panjang jari-jari alas dari suatu tabung yaitu = 10,5 cm serta tingginya = 20 cm. Untuk π = 22/7 hitunglah:

a. Luas selimut tabung

b. Luas tabung tanpa tutup

c. Luas tabung seluruhnya

Jawab:

Diketahui:

• r = 10,5 cm
• t = 20 cm
• π = 22/7

Ditanyakan:

a. Luas selimut ?

b. Luas tabung tanpa tutup ?

c. Luas tabung seluruhnya ?

Jawab:

a. Luas selimut tabung menggunakan rumus: 2πrt, sehingga

Luas selimut tabung = 2 × 22/7 × 10,5 × 20

Luas selimut tabung = 1.320 cm²

b. Luas selimut tanpa tutup menggunakan rumus: πr² + 2πrt, sehingga

Luas selimut tanpa tutup = (22/7×10,5×10,5)+(2×π×10,5×20)

Luas selimut tanpa tutup = 346,5 + 1.320

Luas selimut tanpa tutup = 1.666,5 cm²

c. Luas tabung seluruhnya menggunakan rumus: 2πr(r+t), sehingga

Luas tabung seluruhnya = 2×22/7×10,5×(10,5+20)

Luas tabung seluruhnya = 2.013 cm²

Demikianlah ulasan singkat kali ini yang dapat kami sampaikan terkait bangun ruang. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian ya.