Vektor matematika adalah suatu besaran yang memiliki arah, vektor ini sendiri dapat digambarkan dengan memakai panah yang arahnya akan menunjukkan pada arah vektor. Serta panjang garisnya biasa disebut sebagai besar vektor.
Jika vektor dimulai dari titik A serta berakhir di titik B, maka vektor tersebut dapat ditulis dengan menggunakan sebuah huruf kecil yang di atasnya terdapat sebuah tanda garis atau tanda panah (![]() atau
atau ). Atau juga dapat dengan cara seperti pada gambar di bawah ini:
![]()
Sebagai contoh, vektor ![]() adalah vektor yang berawal dari titik A(x1 . y1) menuju ke titik B(x2 . y2) dapat kita lukiskan koordinat cartesius di bawah.
adalah vektor yang berawal dari titik A(x1 . y1) menuju ke titik B(x2 . y2) dapat kita lukiskan koordinat cartesius di bawah.
Panjang garis sejajar sumbu x merupakan v1 = x2 – x1 serta panjang garis sejajar sumbu y merupakan v2 = y2 – y1 adalah beberapa komponen vektor .
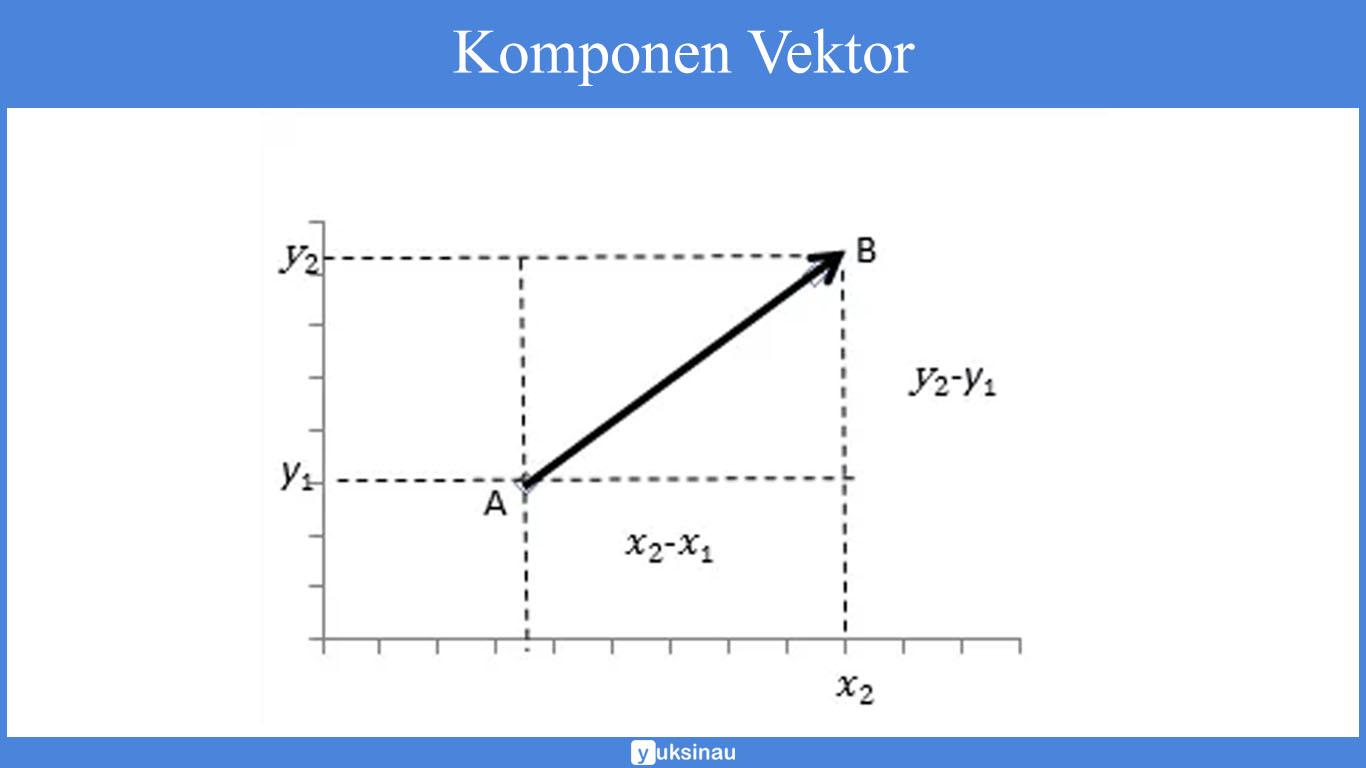
Komponen vektor bisa kita tuliskan guna menyatakan vektor secara aljabar yakni:

Daftar Isi
Jenis Vektor
Terdapat beberapa jenis dari vektor khusus yang ada dalam matematika antara lain:
- Vektor Posisi
Sebuah vektor yang letak dari titik awalnya di titik 0 (0,0) serta titik ujungnya berada di A - Vektor Nol
Sebuah vektor yang di mana panjangnya nol serta dinotasikan dengan. Vektor nol tidak mempunyai arah vektor yang jelas.
- Vektor satuan
Suatu vektor yang memiliki panjangnya satu satuan. Vektor satuan dari yaitu:
yaitu:

- Vektor basis
Vektor basis adalah suatu vektor satuan yang saling tegak lurus. Dalam vektor ruang dua dimensi (R2) memiliki dua vektor basis yakni dan
dan  . Sementara dalam tiga dimensi (R3)mempunyai tiga vektor basis yakni
. Sementara dalam tiga dimensi (R3)mempunyai tiga vektor basis yakni  ,
,  , dan juga
, dan juga  .
.
Macam Macam sekaligus Operasi Vektor
Vektor matematika tak hanya terdiri dari beberapa jenis saja, namun vektor matematika juga terdiri dari beberapa macam.
Nah beriktu akan kami berikan macam-macam vektor beserta dengan operasinya sekaligus, simak baik-baik ya:
Vektor di R2
Panjang dari suatu segmen garis yang menyebutkan vektor dilambangkan dengan memakai ![]() atau dapat juga dinotasikan dengan menggunakan simbol |
atau dapat juga dinotasikan dengan menggunakan simbol |![]() |
|
Berikut ini panjang dari vektor yaitu seperti berikut ini:
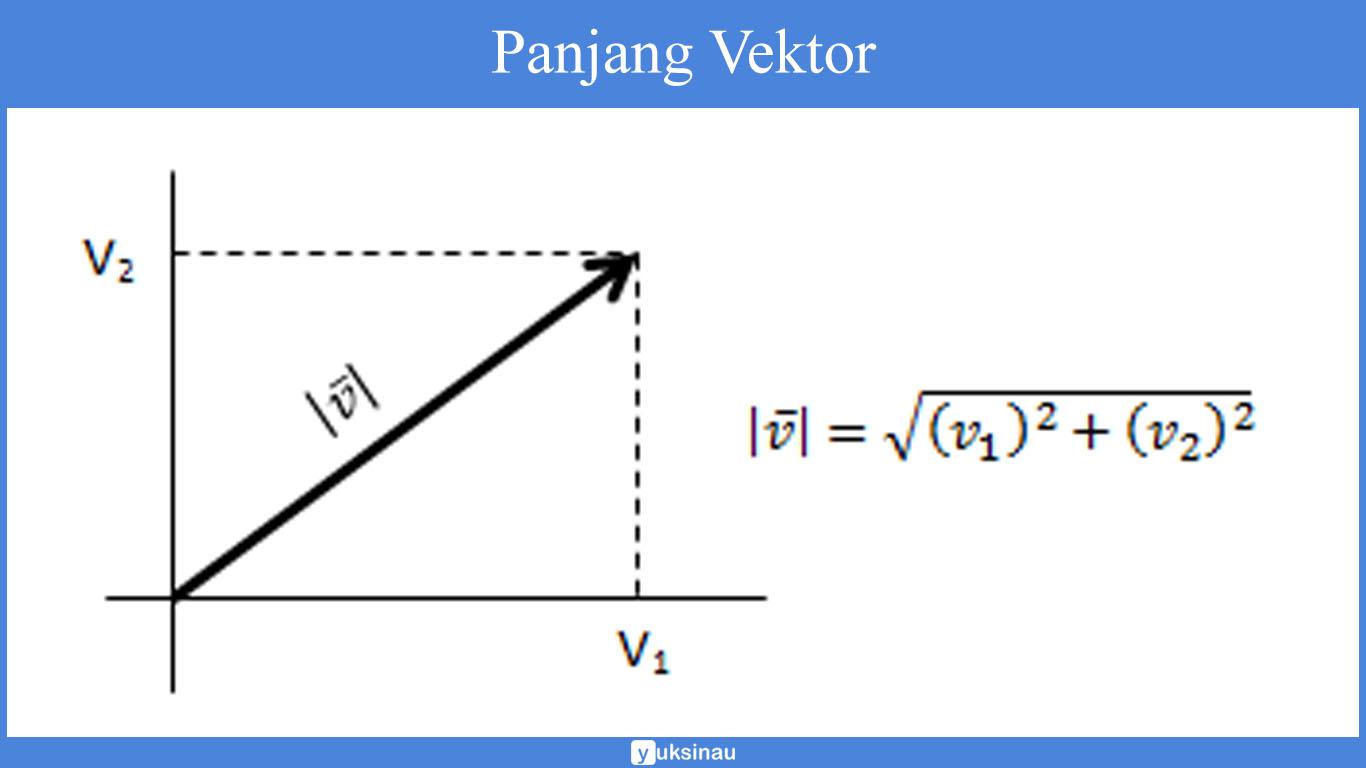
Panjang vektor sendiri adalah bentuk yang bisa dihubungkan dengan sudut ∅ yang dapat dengan mudah untuk dibentuk oleh vektor serta juga sumbu positif.
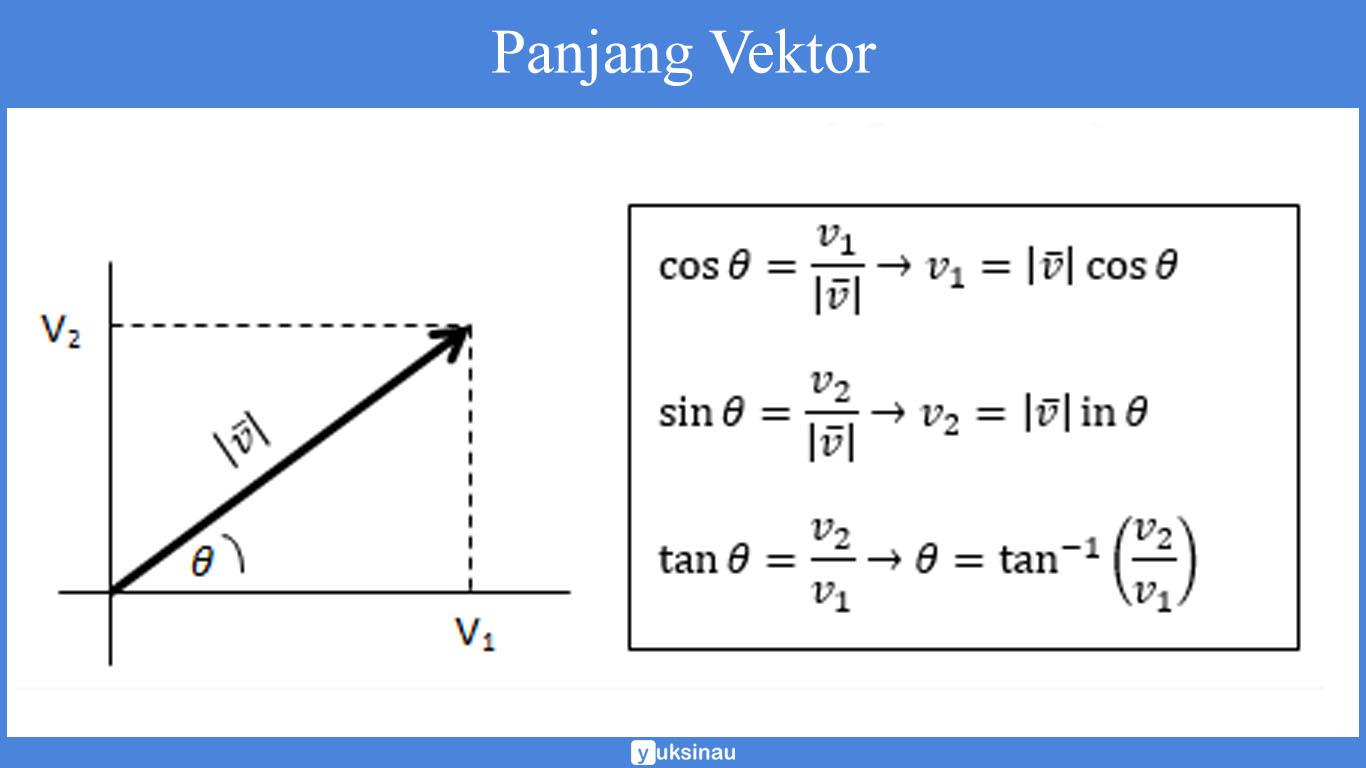
Operasi Vektor di R2
⇒ Proses penjumlahan dan juga Pengurangan Vektor di R2
Resultan adalah sebutan dari hasil penjumlahan yang dilakukan pada dua vektor atau pun lebih.
Penjumlahan pada vektor ini sendiri juga dapat dilakukan secara aljabar serta juga dapat dilakukan dengan memakai cara menjumlahkan komponen yang berada di posisi sama atau seletak.
Apabila:
![]()
maka :
![]()
Maka penjumlahan secara grafis sendiri dapat kita lihat pada contoh gambar yang ada di bawah ini:
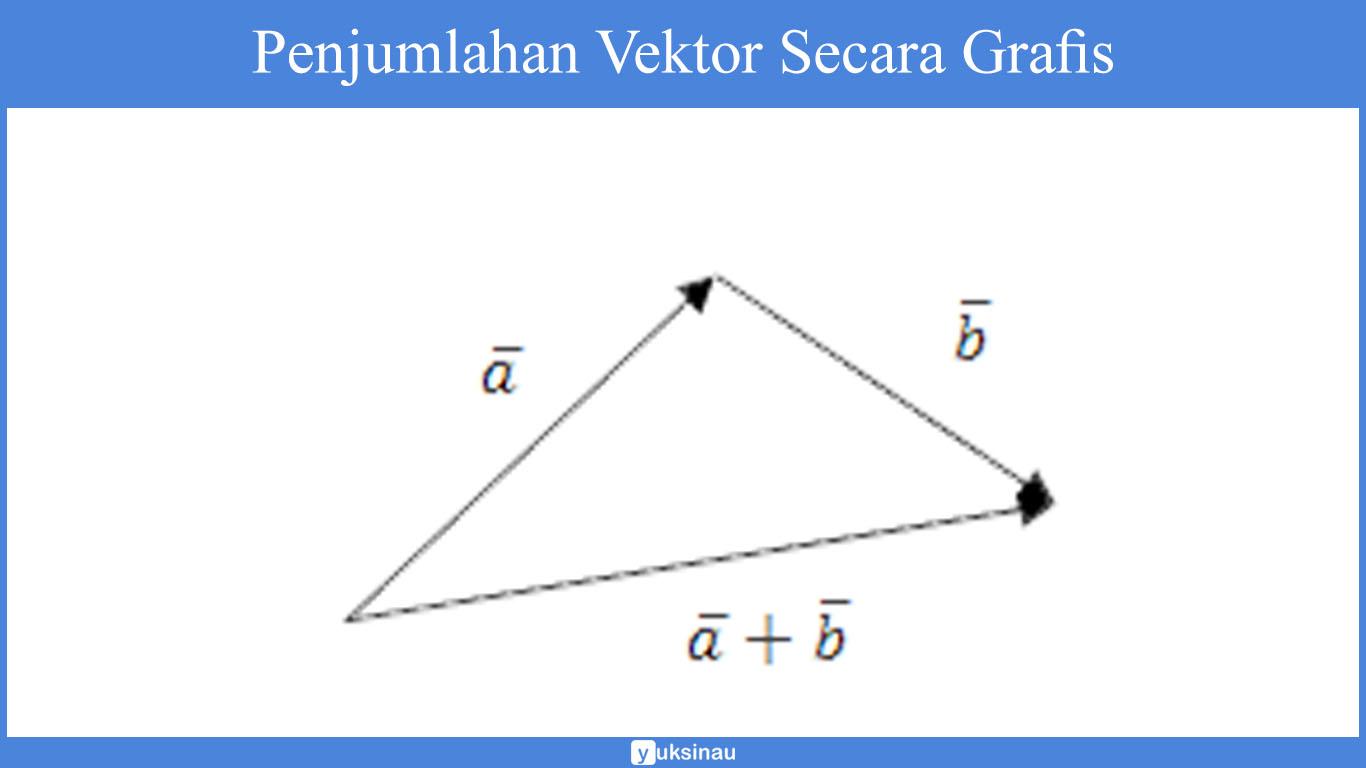
Pada pengurangan vektor ini diberlakukan sama dengan yang ada pada penjumlahan, antara lain adalah sebagai berikut, lihat pada contoh di bawah ini:
![]()
Sifat -sifat di dalam penjumlahan vektor ini sendiri adalah seperti di bawah ini, silahkan disimak rumusnya:
![]()
⇒ Perkalian Vektor di R2 Dengan Skalar
Suatu vektor sendiri juga dapat dikalikan dengan suatu skalar atau bilangan real yangnantinya akan menghasilkan suatu vektor baru jika ![]() adalah vektor dan k merupakan skalar.
adalah vektor dan k merupakan skalar.
Sehingga perkalian vektor dapat dinotasikan menjadi seperti di bawah ini:
![]()
Berikut ini merupakan beberapa keterangan selengkapnya:
- Apabila k > 0, maka vektor
 akan searah dengan vektor
akan searah dengan vektor  .
. - Apabila k < 0, maka vektor
 akan berlawanan arah dengan vektor
akan berlawanan arah dengan vektor  .
. - Apabila k = 0, maka vektor
 merupakan vektor identitas
merupakan vektor identitas  .
.
Jika secara grafis perkalian ini dapat mengubah panjang vektor serta dapat dilihat pada tabel yang terletak di bawah ini:
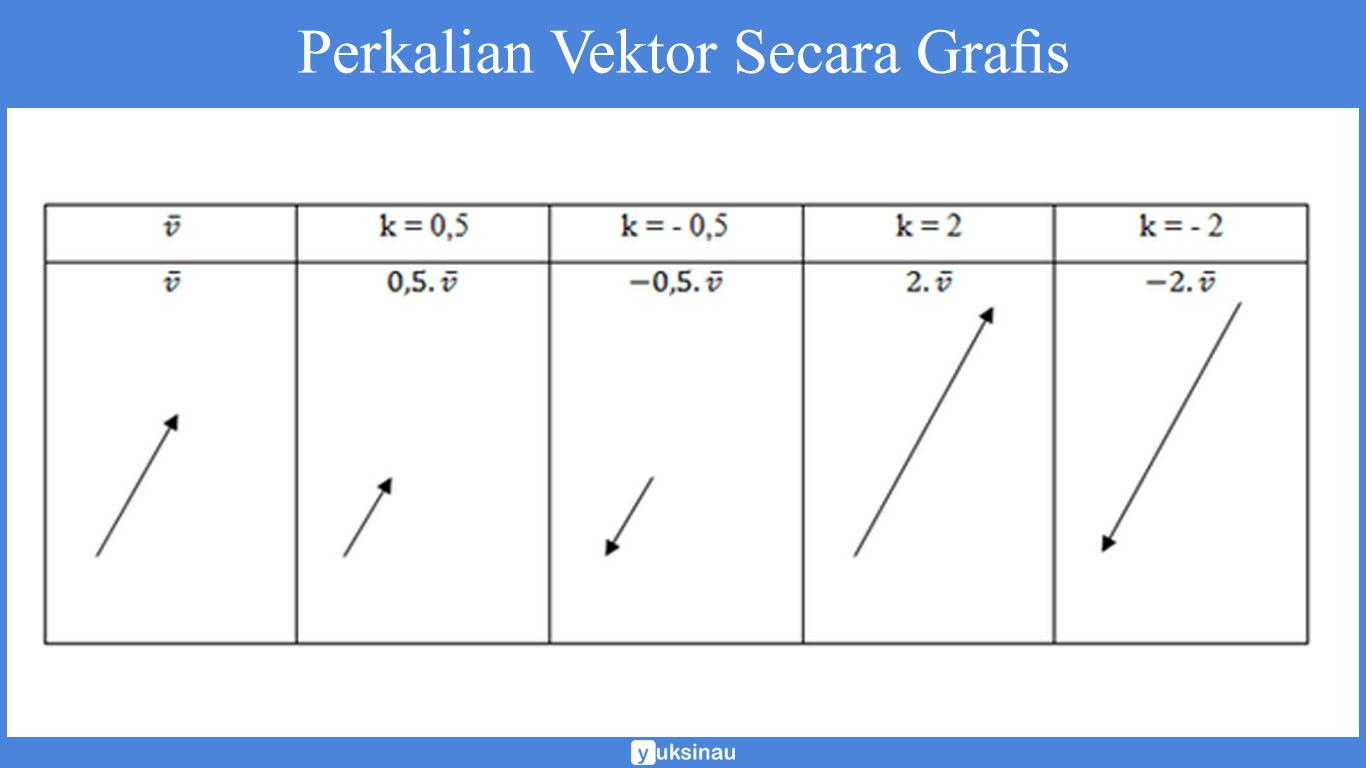
Jika secara aljabar, perkalian vektor ![]() dengan skalar k dapat kita rumukan dengan memakai rumus seperti yang ada di bawah ini:
dengan skalar k dapat kita rumukan dengan memakai rumus seperti yang ada di bawah ini:
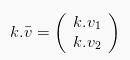
⇒ Perkalian Skalar Dua Vektor di R2
Dalam perkalian skalar dua vektor bisa juga disebut sebagai hasil kali titik dua vektor yang dapat kita tuliskan seperti yang ada di bawah ini:
![]()
Vektor di R3
Vektor yang terelta di dalam ruang tiga dimensi (x, y, z) di mana jarak antara dua titik vektor dalam R3 bisa kalian ketahui dengan pengembangan rumus phytagoras.
Apabila titik dari A(x2. y2. z2) serta B(x2. y2. z2) adalah:
![]()
Atau apabila 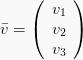 , sehingga:
, sehingga:
![]()
Vektor ![]() bisa disebutkan dalam dua bentuk, yakni dalam kolom
bisa disebutkan dalam dua bentuk, yakni dalam kolom
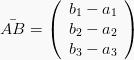 atau dalam baris menjadi
atau dalam baris menjadi ![]()
Vektor juga bisa disajikan sebagai kombinasi linier dari vektor basis seperti ![]() atau
atau ![]() dan atau
dan atau ![]()
berikut selengkapnya:

Operasi Vektor di R3
Operasi vektor di R3 secara umum, mempunyai konsep yang sama dengan operasi yang ada di vektor R2 dalam penjumlahan, pengurangan, hingga perkalian.
Penjumlahan dan pengurangan vektor di R3
Penjumlahan dan juga pengurangan vektor di R3 sama dengan yang ada di vektor R2 yakni:

Perkalian vektor di R3 dengan skalar
Apabila ![]() merupakan vektor dan k merupakan skalar. Maka perkalian vektor menjadi:
merupakan vektor dan k merupakan skalar. Maka perkalian vektor menjadi:
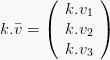
Hasil kali skalar dua vektor
Selain rumus pada R3, terdapat rumus lain dalam hasil kali skalar dua vektor. Apabila ![]() dan
dan ![]() maka
maka ![]() adalah:
adalah:
![]()
Proyeksi Orthogonal vektor
Apabila vektor ā diproyeksikan menjadi vektor barb serta diberi nama ![]() seperti gambar di bawah ini:
seperti gambar di bawah ini:
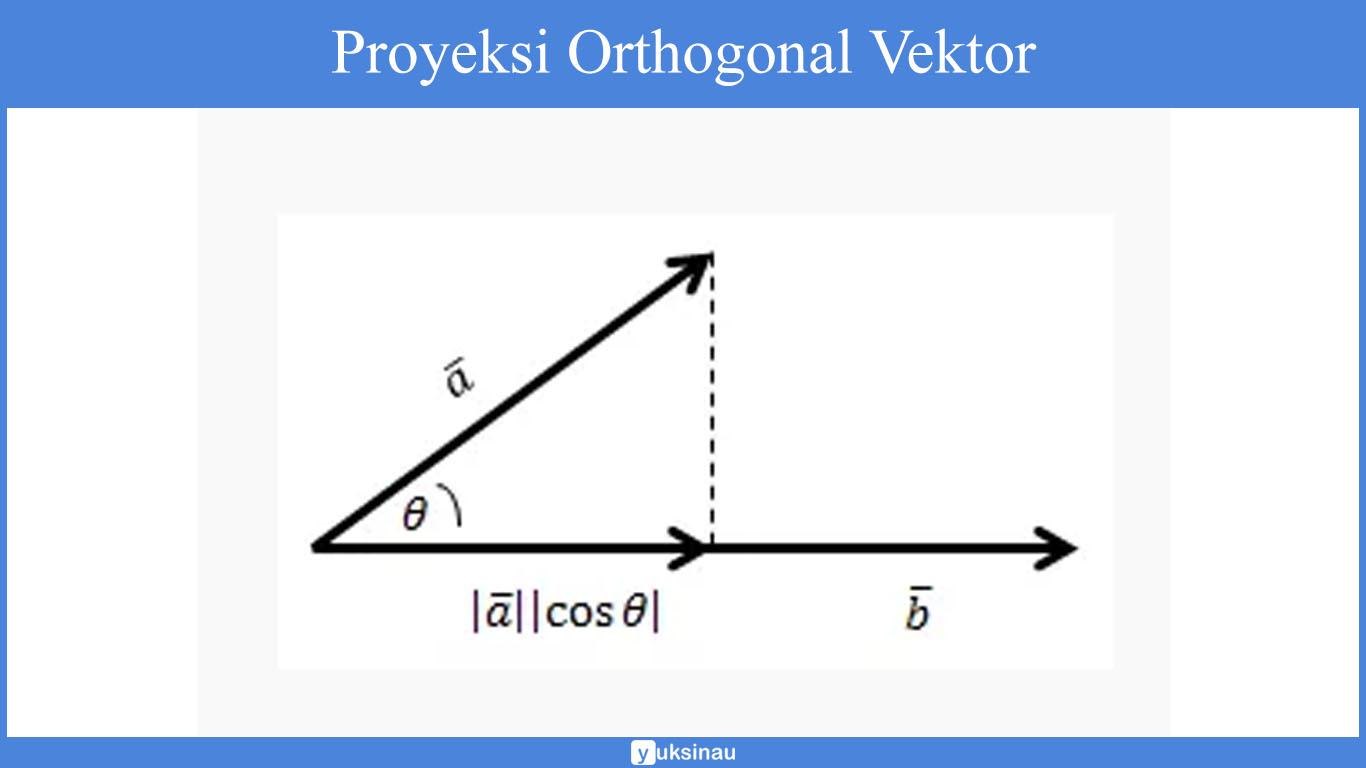
Diketahui:
![]()
Sehingga:
![]()
Untuk memperoleh vektornya:
![]()
Notasi Vektor
Seperti yang telah dijelaskan di atas, vektor disini dinyatakan dengan menggunakan huruf yang diberi arah garis di atasnya.
Vektor bisa dinyatakan dalam dua dimensi bahkan tiga dimensi atau lebih. Apabila dinyatakan dalan tiga dimensi maka vektor mempunyai vektor satuan yang dinyatakan dalam i, j, dan k.
Vektor satuan merupakan vektor yang besarnya satu satuan serta arahnya sesuai dengan sumbu utama, yaitu:
i merupakan vektor satuan yang searah sumbu x (absis)
j merupakan vektor satuan yang searah sumbu y (ordinat)
k merupakan vektor satuan yang searah sumbu z (aplikat)
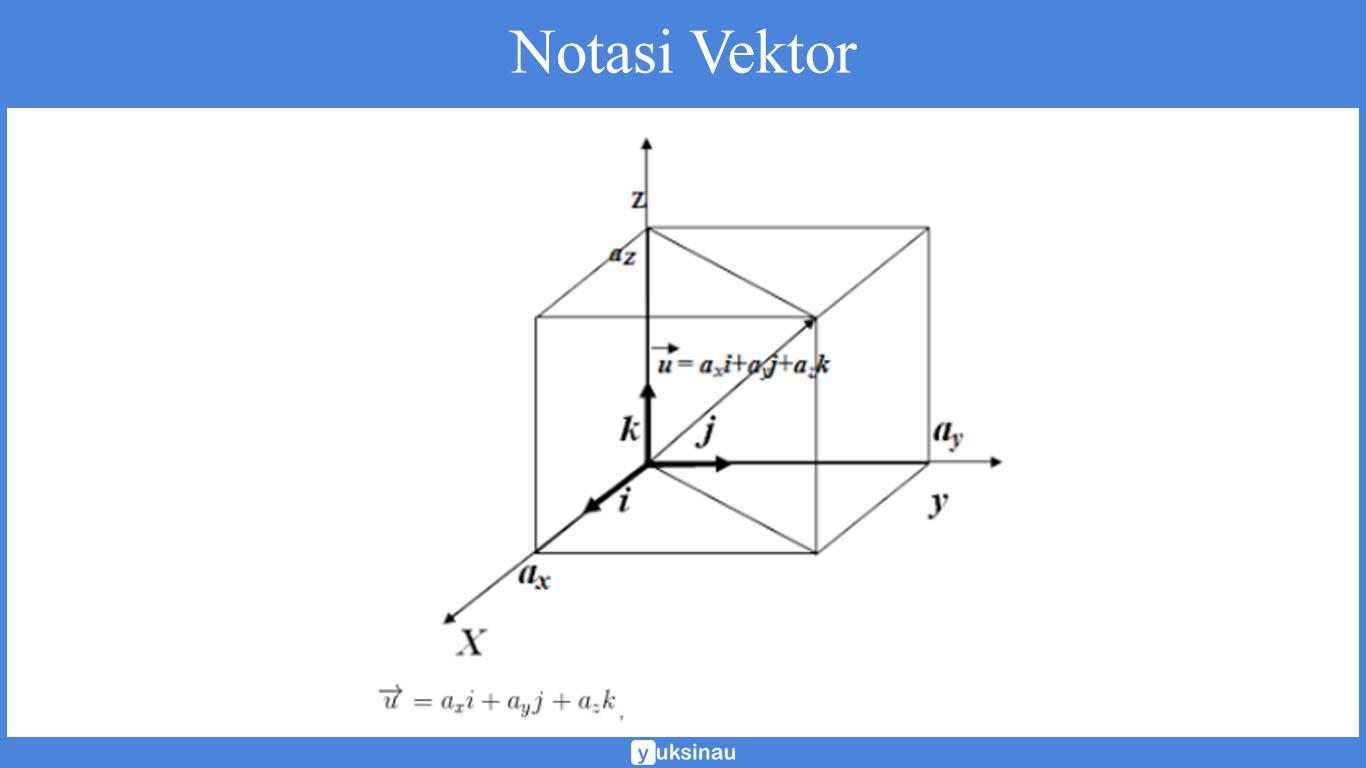
dengan a_x sebagai komponen arah sumbu x, dan a_y komponen arah sumbu y dan a_z merupakan komponen arah sumbu z.
Bentuk tulisan vektor:
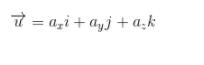
dalam matematika lebih sering dituliskan ke dalam bentuk:
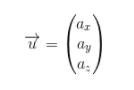
dengan komponen dalam bentuk indeks angka menjadi:
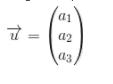
Panjang dari vektor (besar,nilai) dituliskan seperti tanda mutlak yang ada pada aljabar
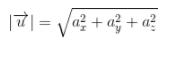
Atau dalam indeks angka
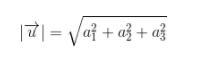
Jika vektor ditentukan oleh koordinat
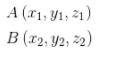
Maka vektor AB dinyatakan dengan
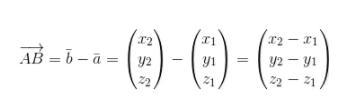
Panjang vektor AB
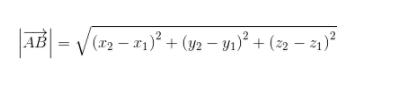
Sementara untuk vektor satuan dari suatu vektor yang dinyatakan sebagai
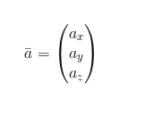
Dinyatakan dengan
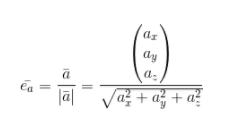
Contoh Soal dan Pembahasan
Soal 1.
Jika diketahui terdapat sebuah titik A(2,4,6), titik B(6,6,2), serta titik C(p,q,-6). Apabila titik A, B serta titik C ini letaknya segaris, carilah berapa nilai dari p + q tersebut!
Jawab:
Jika titik titik A, B dan C ini berada segaris maka vektor ![]() serta vektor
serta vektor ![]() ini juga dapat searah maupun berlainan arah.
ini juga dapat searah maupun berlainan arah.
Sehingga akan terdapat bilangan m yang merupakan sebuah kelipatan serta bisa membentuk persamannya seperti yang ada di bawah ini:
- m.
 =
= 
Apabila B terletak di antara titik A dan C maka akan didapatkan seperti yang ada bawah ini:
![]()
Sehingga akan dapat diperoleh:
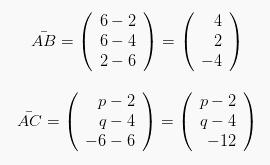
Sehingga dapat ditentukan kelipatan m dalam persamaan:
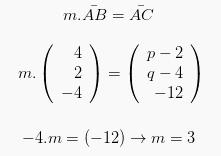
Maka hasil yang akan kita dapatkan yaitu:
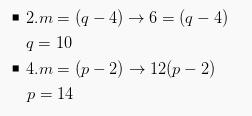
Sehingga bisa kita tarik kesimpulan seperti yang ada di bawah ini:
p + q = 10 + 14 = 24
Soal 2.
Apabila diketahui vektor di titik A dan titik B dan vektor pada titik C yang terletak diantara garis Ab seperti yang ada pada gambar di bawah. Tentukan persamaan dari vektor C.
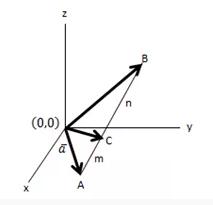
Jawab:
Dari gambar di atas bisa kita ketahui jika:
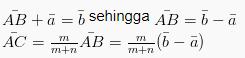
Sehingga:
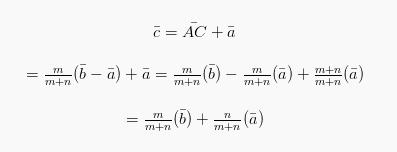
Demikianlah ulasan singkat mengenai vektor matematika yang dapat kami sampaikan. Semoga ulasan di atas mengenai vektor matematika dapat kalian jadikan sebagai bahan belajar kalian.
Satu pemikiran pada “Vektor Matematika”