Statistika merupakan suatu cabang dari matematika yang mempelajari bagaimana cara untuk mengumpulkan data, menyusun data, menyajikan data, mengolah sekaligus menganalisis data, menarik kesimpulan, dan juga menafsirkan parameter.
Selengkapnya mengenai Statistika simak ulasan berikut ini.
Daftar Isi
Statistika
Sehingga apabila kita tarik kesimpulan ada beberapa aktivitas yang ada dalam statistika ini, antara lain:
- Mengumpulkan data
- Menyusun data
- Menyajikan data
- Mengolah dan Menganalisis data
- Menarik kesimpulan
- Menafsirkan
Sebelum mempelajari lebih jauh mengenai statistika, yuk kita ketahui terlebih dahulu hal-hal yang berkaitan dengan statistika.
Statistika merupakan sebuah ilmu yang mempelajari bagaimana merencanakan, mengumpulkan, menganalisis, menginterpretasi, serta mempresentasikan data. -sc:wikipedia
Selengkapnya, simak baik-baik ulasan berikut ini mengenai Statistika.
Datum dan Data
Saat kita berada di bangku kelas IX, maka kita sudah mempelajari apa itu pengertian datum dan data.
Untuk mengingatnya kembali, perhatikan penjelasan di bawah ini.
Sebagai contoh, hasil pengukuran berat badan dari 5 murid yaitu 43 kg, 46 kg, 44 kg, 55 kg, dan 60 kg.
Serta tingkat kesehatan dari kelima murid itu antara lain yaitu baik, baik, baik, buruk, dan buruk.
Data pengukuran berat badan dari uraian di atas yaitu 43 kg, 46 kg, 44 kg, 55 kg, dan 60 kg dan data tersebut disebut sebagai fakta dalam bentuk angka.
Sementara untuk hasil pemeriksaan kesehatan yang tertera baik dan buruk disebut sebagai fakta dalam bentuk kategori.
Kemudian, fakta tunggal dinamakan sebagai datum. Adapun kumpulan datum yang disebut sebagai data.
Populasi dan Sampel
Sebagai contoh ada peneliti yang ingin meneliti mengenai tinggi badan rata-rata siswa SMA yang ada di kota Jakarta Barat.
Lalu, sang peneliti tersebut mengumpulkan data mengenai tinggi badan seluruh siswa SMA yang ada di kota Jakarta Barat.
Data tinggi badan dari semua siswa SMA di kota Jakarta Barat di sebut sebagai populasi.
Tetapi, sebab terdapat beberapa kendala yang berupa keterbatasan waktu serta biaya, maka data tinggi badan dari keseluruhan siswa SMA di kota Jakarta Barat akan sulit untuk didapatkan.
Sehingga solusi dari kendala tersebut adalah melakukan pengambilan tinggi badan dari beberapa siswa SMA di kota Jakarta Barat yang bisa mewakili keseluruhan siswa SMA di kota Jakarta Barat.
Data tersebutlah yang disebut sebagai data dengan nilai perkiraan, sementara untuk sebagian siswa SMA yang dijadikan objek penelitian disebut sebagai sampel.
Supaya didapatkan hasil yang berlaku secara umum maka dalam pengambilan sampel, diusahakan supaya sampel yang digunakan bisa untuk mewakili populasi.
Pengumpulan Data
Berdasarkan dari sifatnya, data dibagi menjadi 2 macam golongan, antara laing yakni:
1) Data kuantitatif merupakan data yang berwujud angka atau bilangan. Data kuantitatif terbagi menjadi dua bagian, antara lain yaitu data cacahan dan data ukuran. Berikut penjelasannya:
- Data cacahan (data diskrit) merupakan suatu data yang didapatkan dengan cara membilang. Sebagai contoh, data mengenai banyak anak dalam keluarga.
- Data ukuran (data kontinu) merupakan data yang didapatkan dengan cara mengukur. Sebagai contoh, data mengenai ukuran tinggi badan murid.
2) Data kualitatif merupakan suatu data yang bukan berupa bilangan.
Data kualitatif dapat berwujud ciri, sifat, atau gambaran dari kualitas objek. Sebagai contohnya, data yang berkaitan dengan kualitas pelayanan seperti baik, sedang, dan kurang.
Cara untuk mengumpulkan data, antara lain yakni dengan melakukan wawancara, mengisi lembar pertanyaan (questionery), melakukan pengamatan (observasi), atau memakai berbagai data yang sudah ada. Contohnya rataan hitung nilai rapor.
Menyajikan Data dalam Bentuk Diagram (Statistika)
1. Diagram Garis
Penyajian data statistik dengan memakai diagram berbentuk garis lurus disebut dengan diagram garis lurus atau diagram garis.
Diagram garis pada umumnya dimanfaatkan guna menyajikan data statistik yang didapatkan berdasarkan pengamatan dari masa ke masa secara berurutan.
Sebagai contoh: simulasi diagram garis yang biasa kalian ubah dari diagram garis yang ada.
2. Diagram Batang
Diagram batang pada umumnya dipakai untuk menggambarkan perkembangan nilai dari sebuag objek penelitian dalam kurun waktu tertentu.
Diagram batang menggambarkan berbagai keterangan dengan berabgai gambar batang tegak atau mendatar dan sama lebar dengan batang-batang terpisah.
3. Diagram Lingkaran
Diagram lingkaran merupakan penyajian data statistik dengan memakai gambar yang berbentuk lingkaran.
Setiap bagian yang berasal dari daerah lingkaran akan menunjukkan bagian-bagian atau persen dari keseluruhan data.
Untuk membuat diagram lingkaran, maka langkah yang harus kalian terlebih dahulu adalah menentukan besarnya persentase pada masing-masing objek terhadap keseluruhan data.
Serta besarnya sudut pusat sektor lingkaran.
Penyajian Data dalam Bentuk Tabel Distribusi Histogram, Poligon dan Ogive
1. Distribusi Frekuensi Tunggal
Data tunggal seringkali disbeut sebagai bentuk daftar bilangan. Tetapi terkadang bisa juga dinyatakan di dalam bentuk tabel distribusi frekuensi.
Tabel distribusi frekuensi tunggal adalah cara untuk menyusun data yang relatif sedikit.
2. Distribusi Frekuensi Kelompok
Data yang berukuran besar (n > 30) lebih pas untuk disajikan dalam bentuk tabel distribusi frekuensi kelompok.
Dimana penyajian tabel distribusi frekuensi kelompok adalah suatu cara penyajian data yang dimana akan menyusun datanya dalam kelas-kelas tertentu.
Adapun beberapa tahapan untuk menyusun tabel distribusi frekuensi diantaranya adalah sebagai berikut:
- Langkah ke-1 adalah menentukan Jangkauan (J) = Xmax – Xmin
- Langkah ke-2 yaitu menentukan banyak interval (K) dengan menggunakan rumus “Sturgess”. Yakni: K= 1 + 3,3 log n dengan n merupakan banyak data.
Banyak kelas harus merupakan bilangan bulat positif dari hasil pembulatan ke bawah. - Langkah ke-3 adalah menentukan panjang interval kelas (I) dengan memakai rumus:
J
I = ––––
K - Langkah ke-4 menentukan batas-batas kelas. Data terkecil harus merupakan batas dari bawah interval kelas pertama atau data terbesar yang merupakan batas atas interval kelas terakhir.
- Langkah ke-5 yaitu memasukkan berbagai data ke dalam kelas-kelas yang sesuai. Serta menentukan nilai frekuensi pada masing-masing kelas dengan sistem turus.
3. Histogram
Dari sebuah data yang kita dapatkan bisa kita susun ke dalam tabel distribusi frekuensi serta kita sajikan ke dalam bentuk diagram yang disebut sebagai histogram.
Apabila dalam diagram batang, gambar batang-batangnya terpisah, maka lain halnya yang ada pada histogram gambar batang-batangnya berimpit.
4. Poligon
Apabila pada titik-titik tengah dari histogram dihubungkan dengan garis serta gamabr batangnya dihapus, maka akan kita dapatkan poligon frekuensi.
Berdasarkan dari contoh di atas bisa kta buat poligon frekuensinya.
5. Distribusi Frekuensi Kumulatif
Daftar distribusi kumulatif di bagi menjadi dua macam, diantaranya adalah sebagai berikut ini:
a. Daftar distribusi kumulatif kurang dari (memakai tepi atas).
b. Daftar distribusi kumulatif lebih dari (memakai tepi bawah).
Untuk lebih jelasnya, perhatikan contoh data berikut ini.`
6. Ogive (Ogif)
Grafik yang menggambarkan frekuensi kumulatif kurang dari atau frekuensi kumulatif lebih dari disebut sebagai poligon kumulatif.
Poligon kumulatif cara dibikin semulus, yang hasilnya disebut dengan ogif.
Terdapat dua macam ogif, antara lain:
a. Ogif frekuensi kumulatif kurang dari disebut sebagai ogif positif.
b. Ogif frekuensi kumulatif lebih dari disebut sebagai ogif negatif.
Median
2. Median
1) Median untuk data tunggal
Median merupakan sebuah nilai tengah yang sudah diurutkan. Median dilambangkan sebagai Me.
Untuk menentukan nilai Median dari data tunggal bisa dengan menggunakan cara di bawah ini:
- Mengurutkan data lalu kita cari nilai tengah,
- Apabila banyaknya data besar, sesudah kita mengurutkan datanya, maka selanjutnya kita terapkan rumus di bawah ini:
Untuk ganjil: Me = x1/2(n-1)
Untuk genap: Me = Xn/2 + Xn/2+1
––––––––––––
2
Keterangan:
xn/2 = data pada urutan ke-n/2 sesudah diurutkan.
Sebagai contoh:
Tentukanlah median dari data di bawah ini:
2, 5, 4, 5, 6, 7, 5, 9, 8, 4, 6, 7, 8
Jawab:
Maka kita urutkan data di atas menjadi:
2, 4, 4, 5, 5, 5, 6, 6, 7, 7, 8, 8, 9
Sehingga kita temukan median = data ke-(13 + 1)/2 = data ke-7
Sehingga jawaban untuk mediannya = 6
2) Median untuk data kelompok
Apabila data yang tersedia adalah data kelompok hal itu berarti data itu dikelompokkan ke dalam berabgai interval kelas yang sama panjang.
Untuk mengetahui nilai dari mediannya bisa kita tentukan dengan menggunakan rumus berikut ini.

Keterangan:
Kelas median merupakan suatu kelas yang ada dalam data X1/2 n
- L = tepi bawah kelas median
- c = lebar kelas
- n = banyaknya data
- F = frekuensi kumulatif kurang dari sebelum kelas median
- f = frekuensi kelas median
Modus
Modus merupakan suatu nilai yang paling sering atau banyak muncul atau nilai yang memiliki frekuensi tertinggi.
Apabila sebuah data hanya memiliki satu modus disebut unimodal seta jika mempunyai dua modus disebut sebagai bimodal.
Sementara apabila mempunyai modus lebih dari dua disebut seabgai multimodal. Modus dilambangkan sebagai Mo.
1) Modus data tunggal
Modus dari data tunggal merupakan data yang sering muncul atau data dengan frekuensi tertinggi.
Perhatikan contoh soal yang ada di bawah ini:
Contoh:
Tentukanlah modus dari data yang disajikan di bawah ini:
2, 1, 4, 1, 1, 5, 7, 8, 9, 5, 5, 10
Jawab:
Data yang sering muncul yaitu 1 dan 5. Sehingga modus dari data di atas adalah 1 dan 5.
2. Modus data kelompok
Modus data kelompok biasa dirumuskan dengan rumus seperti berikut ini:

Keterangan:
- L = tepi bawah kelas modus
- c = lebar kelas
- d1 = selisih frekuensi dari kelas modus dengan kelas sebelumnya
- d2 = selisih frekuensi dari kelas modus dengan kelas sesudahnya
Kuartil
Kuartil (Q)
Seperti yang telah kita bahas sebelumnya, bahwa median akan membagi data yang sudah diurutkan menjadi dua bagian yang sama banyak.
Adapula kuartil yang mana berfungsi untuk membagi data yang sudah diurutkan menjadi empat bagian yang sama banyak.
1) Kuartil data tunggal
Urutkan data dari yang kecil ke yang besar, lalu menentukan kuartil dengan menggunakan rumus seperti berikut ini:

Contoh soal:
Tentukanlah nilai dari Q1, Q2, dan Q3 dari data berikut: 3, 4, 7, 8, 7, 4, 8, 4, 6, 9, 10, 8, 3, 7, 12.
Jawab:
Langkah 1: urutkan data dari yang terkecil ke terbesar sehingga akan kita dapatkan data menjadi:
3, 3, 4, 4, 4, 6, 7, 7, 7, 8, 8, 8, 9, 10, 12.
1(15+1)
Langkah 2: Letak data Q1=–––––––– = 4
4
Sehingga nilai dari Q1 berada pada data ke-empat yakni 4
2(15+1)
Langkah 3: Letak data Q2=–––––––– = 8
4
Sehingga nilai dari Q2 berada pada data ke-delapan yakni 7
3(15+1)
Langkah 4: Letak data Q1=–––––––– = 12
4
Sehingga nilai dari Q3 berada pada data ke-duabelas yakni 8
2) Kuartil data kelompok
Nilai kuartil biasa dirumuskan seperti berikut ini:

Keterangan:
- Qi = kuartil ke-i (1, 2, atau 3)
- L = tepi bawah kelas kuartil ke-i
- n = banyaknya data
- F = frekuensi kumulatif kelas sebelum kelas kuartil
- c = lebar kelas
- f = frekuensi kelas kuartil
Desil dan persentil
Desil berfungsi untuk membagi data menjadi sepuluh bagian yang sama besar. Sementara persentil berfungsi untuk membagi data menjadi 100 bagian yang sama.
Desil dan persentil data tunggal
Desil
![]()
Keterangan:
Di = desil ke-i
i = 1, 2, 3, . . ., 9
n = banyaknya data
Persentil
![]()
Keterangan:
Pi = persentil ke-i
i = 1, 2, 3, . . ., 99
n = banyaknya data
Ukuran Penyebaran Data
Ukuran pemusatan atau yang biasa disebut seabgai mean, median dan modus, adalah informasi yang memberikan penjelasan kecenderungan data sebagai wakil dari beberapa data yang ada.
Adapun ukuran dari penyebaran data yang menyajikan gambaran seberapa besar data yang menyebar dari titik-titik pemusatan.
1. Jangkauan (Range)
Ukuran penyebaran yang paling sederhana (kasar) merupakan jangkauan (range) atau rentangan nilai, yakni selisih antara data terbesar dan data terkecil.
1) Range data tunggal
Untuk range data tunggal bisa dirumuskan dengan rumus:
R = Xmaks – Xmin
Contoh :
Tentukan range dari data yang disajikan di bawah ini.
6, 7, 3, 4, 8, 3, 7, 6, 10, 15, 20
Jawab:
Dari data di atas maka kita dapatkan xmaks = 20 dan xmin = 3
Sehingga, R = xmaks – xmin adalah = 20 – 3 = 17
2) Range data kelompok
Untuk data kelompok, nilai tertinggi akan diambil dari nilai tengah kelas tertinggi dan juga nilai terendah yang diambil dari nilai kelas yang terendah.
2. Simpangan Rata-Rata (Deviasi Rata-Rata)
Simpangan rata-rata sebuah data yang merupakan nilai rata-rata dari selisih pada masing-masing data dengan nilai rataan hitung.
1) Simpangan rata-rata data tunggal
Simpangan rata-rata data tunggal biasa dirumuskan dengan rumus sebagai berikut:

2) Simpangan rata-rata data kelompok
Simpangan rata-rata data kelompok biasa dirumuskan dengan rumus sebagai berikut:

3. Simpangan Baku (Deviasi Standar) dan Ragam
Sebelum membahas simpangan baku atau juga disebut seabgai deviasi standar, perhatikan baik-baik contoh berikut. ini:
Kalian tentu tahu bahwa masing-masing orang menggunakan sepatu dengan ukuran yang berbeda-beda.
Ada yang menggunakan ukuran 30, 32, 33, … , 39, 40, hingga 41. Perbedaan ini kemudian dimanfaatkan oleh para ahli statistika untuk melihat penyebaran data dalam sebuah populasi.
Perbedaan ukuran sepatu pada umumnya berkaitan erat dengan tinggi badan manusia.
Seorang ahli matematika asal Jerman yang bernama Karl Ganss mempelajari penyebaran dari berbagai macam data.
Beliau kemudian menemukan istilah deviasi standar untuk menerangkan penyebaran yang terjadi. Sekarang ini, ilmuwan sudah memakai deviasi standar atau simpangan baku untuk mengestimasi akurasi pengukuran.
Deviasi standar merupakan akar dari jumlah kuadrat deviasi dibagi dengan banyaknya data.
1) Simpangan baku serta ragam data tunggal
Simpangan baku atau juga disebut sebagai deviasi standar data tunggal biasa dirumuskan dengan rumus sebagai berikut:

2) Ragam dan Simpangan baku data kelompok Ragam
Ragam serta Simpangan Baku merupakan salah satu bagian dari statistik penyebaran data.
Untuk kali ini kita akan melihat bagaimana cara untuk menghitung varian serta standar dari deviasi data kelompok.
Harus kalian ketahui bahwa varian atau variansi merupakan sebutan atau nama lain dari ragam. Sedangkan untuk Simpangan Baku merupakan nama lain dari standar deviasi.
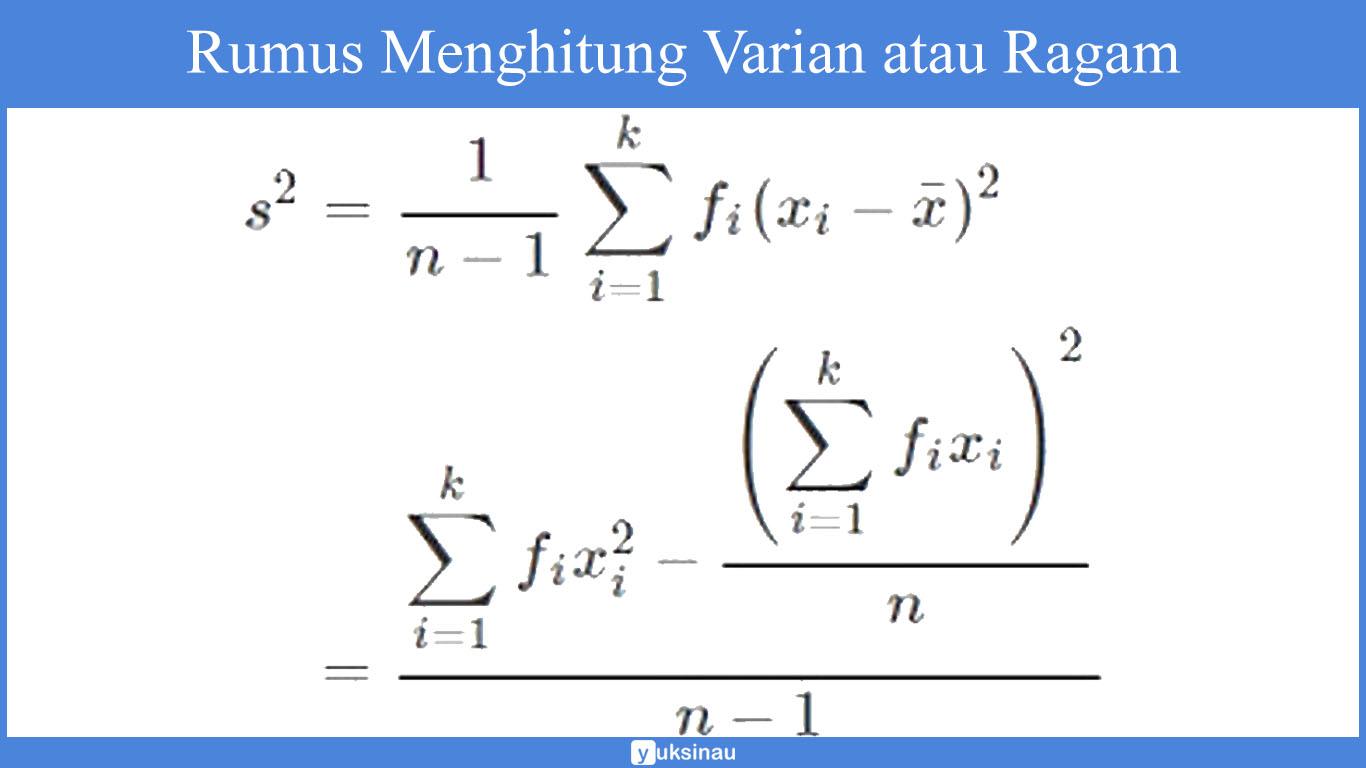
Rumus yang dipakai untuk menghitung ragam serta simpangan baku ini antara lain:
Rumus Menghitung Varian atau Ragam
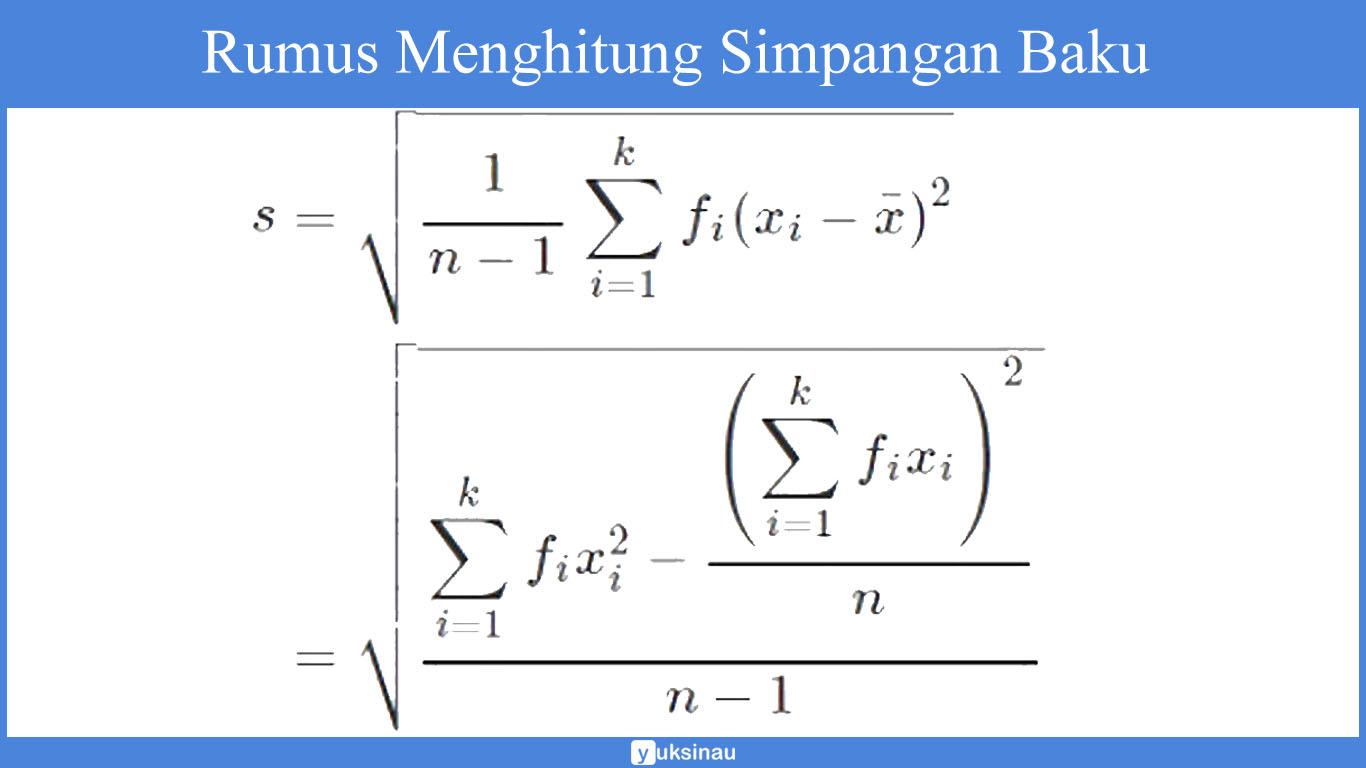
Rumus Menghitung Simpangan Baku atau Standar Deviasi
Soal dan Pembahasan (Statistika)
Soal 1.
Disajikan data sebagai berikut: 6, 7, 7, 8, 9, 8, 6, 7, 8, 5, 9, 4
Kemudian tentukan modus dari data yang telah disajikan di atas!
Jawab:
Terlihat yang paling banyak tampil atau muncul adalah 7 dan 8. Di mana masing-masing sama sebanyak 3 kali muncul. Sehingga dapat kita ketahui bahwa modusnya adalah 7 dan 8.
Soal 2.
Disajikan data dari nilai ujian matematika anak kelas XI IPA-1 seperti berikut ini: 7, 8, 8, 6, 8, 6, 9, 7, 6, 8, 5, 8
Maka tentukan nilai dari modus data yang disajikan di atas!
Jawab:
Modus yang diambil dari data yang paling banyak tampil atau muncul. Dari data di atas maka dapat kita ketahui bahwa modusnya adalah 8.
Soal 3.
Perhatikan data yang disajikan di bawah ini:
7, 8, 9, 10, 5, 4, 2, 3, 1
Tentukan nilai modus datanya!
Jawab:
Data ini tidak mempunyai modus, sebab tidak ada suatu nilai yang muncul lebih sering dari yang lain. Semuanya memiliki frekuensi sama.
Soal 4.
Perhatikan tabel distribusi frekuensi data tunggal di bawah ini:
| Nilai | frekuensi (f) |
| 5 6 7 8 9 | 1 5 11 8 4 |
Tentukan modus dari data di atas!
Jawab:
Yang paling banyak muncul atau modusnya adalah 7. Karena muncul sebanyak 11 kali. Sehingga dapat kita ketahui modusnya adalah 7.
Soal 5. (Statistika – UN Matematika SMA Tahun 2007)
Perhatikan tabel berikut!
| Berat (kg) | Frekuensi |
| 31 – 36 37 – 42 43 – 48 49 – 54 55 – 60 61 – 66 67 – 72 | 4 6 9 14 10 5 2 |
Modus data pada tabel tersebut adalah….
A. 49,06 kg
B. 50,20 kg
C. 50,70 kg
D. 51,33 kg
E. 51,83 kg
Jawab:
Rumus untuk menentukan modus dari data berkelompok:
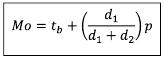
Keterangan:
tb = titik bawah kelas modus
d1 = selisih frekuensi kelas modus dengan frekuensi kelas sebelumnya
d2 = selisih frekuensi kelas modus dengan frekuensi kelas sesudahnya
p = panjang kelas
Dari tabel soal maka kita dapatkan kelas modusnya yaitu interval 49 – 54 (yang frekuensinya paling banyak), data lainnya adalah:
tb = 49 − 0,5 = 48,5
d1 = 14 − 9 = 5
d2 = 14 − 10 = 4
p = 36,5 − 30,5 = 6
Sehingga kita ketahui modusnya yaitu:
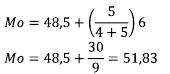
Soal 6. (UN Matematika 2012 – Program IPS)
Data di samping adalah data skor hasil ulangan matematika kelas XII IPS suatu SMA.
| Skor | Frekuensi |
| 21 – 25 26 – 30 31 – 35 36 – 40 41 – 45 46 – 50 | 5 8 12 18 16 5 |
Modus dari data pada tabel adalah…
A. 36,75
B. 37,25
C. 38,00
D. 38,50
E. 39,25
Jawab:
Menentukan modus data:
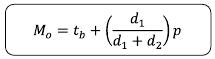

Soal 7.
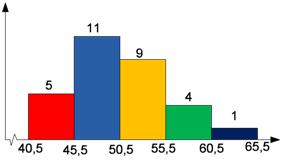
Perhatikan histogram berikut yang menyajikan data berat badan (dalam kg) 30 orang siswa. Modus data tersebut adalah…
A. 47,5
B. 48,25
C. 48,75
D. 49,25
E. 49,75
Jawab:
Perhatikan perbedaan model ini dengan soal sebelumnya, yaitu pada pengambilan panjang interval kelas dan titik bawah kelas modus.
Untuk model soal ini tb = 45,5 (tidak perlu dikurangi 0,5 lagi, karena sudah menyajikan titik bawah secara langsung pada datanya) dan panjang kelasnya p = 50,5 − 45,5 = 5.
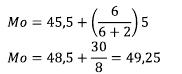
Demikianlah ulasan singkat mengenai Statistika yang dapat kami sampaikan. Semoga ulasan di atas mengenai Statistika dapat kalian jadikan sebagai bahan belajar kalian.