Program linear merupakan salah satu materi matematika yang mengulas pasal optimasi. Masalah yang ada di dalam program linear pada umumnya berhubungan dengan memaksimalkan untung atau meminimalkan biaya produksi.
Tujuan dari program linear ini sangatlah jelas, yakni untuk memperoleh perhitungan yang tepat yang berhubungan dengan biaya yang dianggarkan.
Sebelum kita membahas soal program linear matematika SMA. Yuk ketahui dulu apa saja yang ada dalam program linear matematika sma dan pembahasannya. Selengkapnya simak pembahasan di bawah ini.
Materi program linear yang akan dibahas dalam artikel kali ini meliputi sistem pertidaksamaan linear, model matematika, serta metode untuk menyelesaikan masalah sehubung dengan program linear. Simak baik-baik artikel ini sampai selesai ya.
Daftar Isi
Sistem Pertidaksamaan Linear
Pertidaksamaan linear adalah suatu pertidaksamaan dengan kombinasi operasi antar variabel yang ditandai dengan adanya simbol atau tanda (kurang dari),
(kurang dari sama dengan),
(lebih dari), maupun simbol
(lebih dari sama dengan).
Sementara untuk gabungan dari beberapa pertidaksamaan linear disebut sebagai sistem pertidaksamaan linear.
Sistem pertidaksamaan linear yang ada di program linear akan diajarkan pada tingkat SMA yang pada umumnya akan melibatkan dua variabel dengan dua atau lebih pertidaksamaan linear.
Bagian ini menjadi dasar untuk bisa menyelesaikan problem yang berhubungan dengan program linear.
Salah satu langkah penting dalam sistem pertidaksamaan linear dalam pembahasan mengenai program linear ialah bisa secara tepat menggambarkan garis. Serta daerah yang memenuhi pada bidang kartesius.
Program linear merupakan metode penentuan nilai optimum dari persoalan linear. Nilai optimum didapat dari nilai dalam suatu himpunan penyelesaiaan persoalan linear.
Di bagian ini, kalian akan fokus mempelajari mengenai bagaimana cara untuk menentukan dua langkah tersebut.
Namun sebelum itu, ingat kembali sistem pertidaksamaan linear yang akan kami berikan contoh di bawah ini.
Contoh sistem pertidaksamaan linear
x + y = ≤ 5
2x + y < 7
x + 3y ≥ 11
Cara menggambar persamaan garis lurus sekaligus menentukan daerah yang memenuhi, yaitu:
Himpunan penyelesaian sebuah pertidaksamaan linear dua peubah bisa kita tentukan dengan menggunakan cara seperti berikut ini:
1. Gambarlah garis ax + by = c pada bidang kartesius
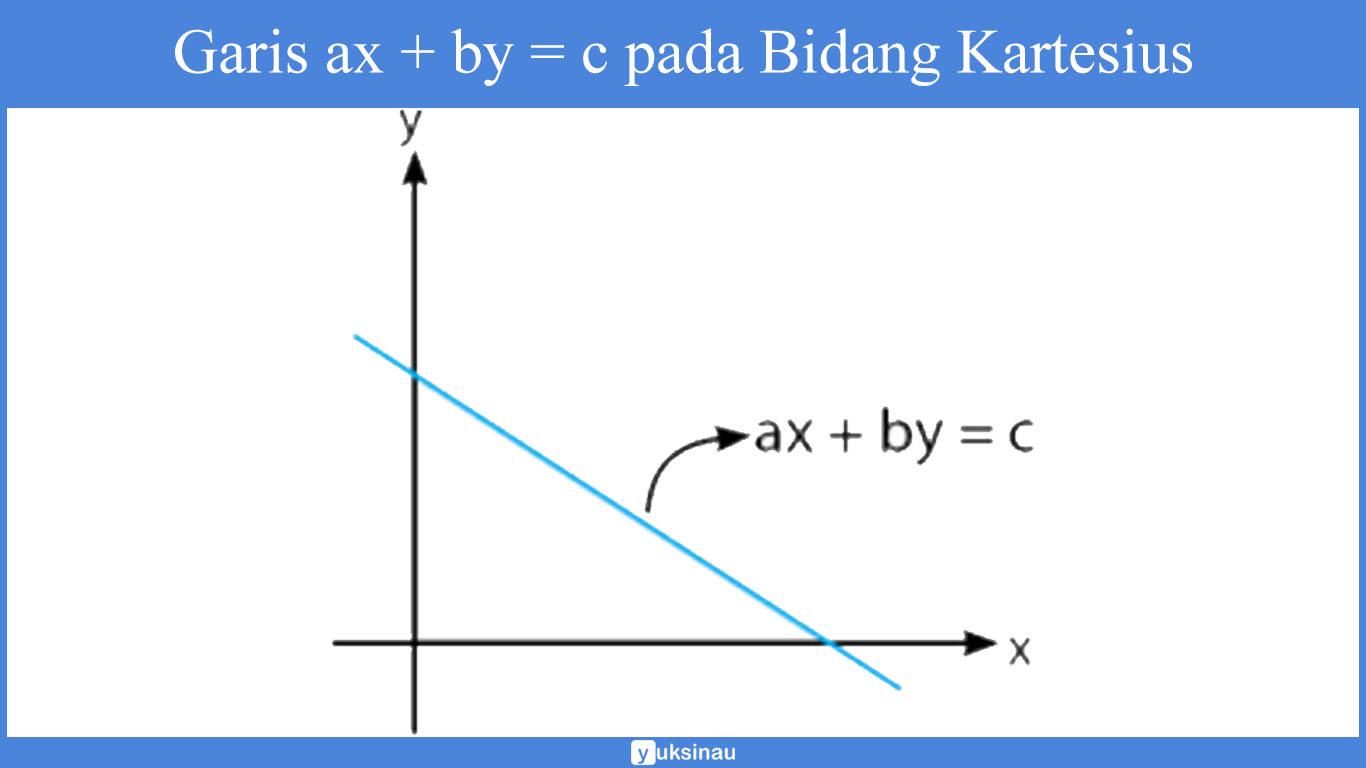
2. Kita ambil sembarang titik untuk (x1.y1) di luar garis ax + by = c lalu hitunglah nilai dari ax1 + by1 serta bandingkan dengan nilai c.
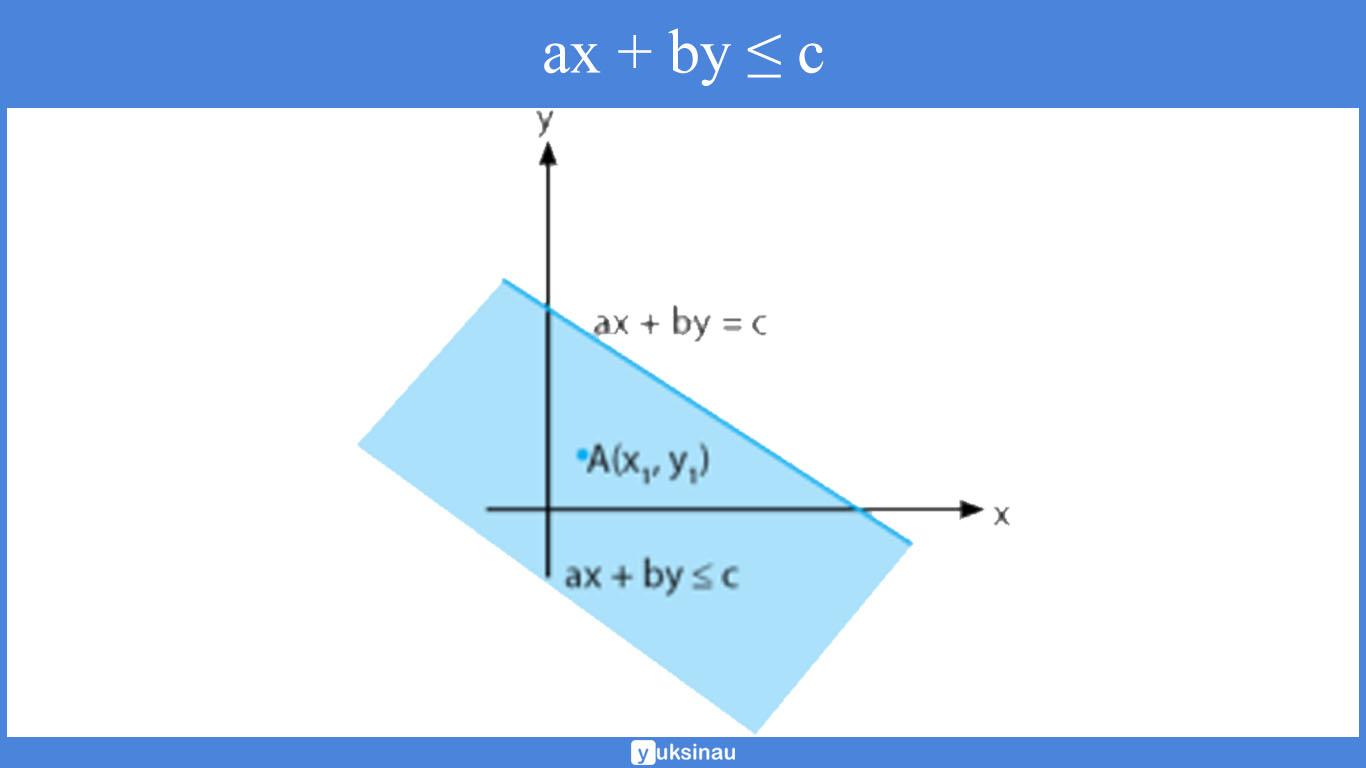
- Apabila ax1 + by1 ≤ c daerah yang memuat x1.y1 merupakan daerah penyelesaian dari pertidaksamaan ax + by ≤ c
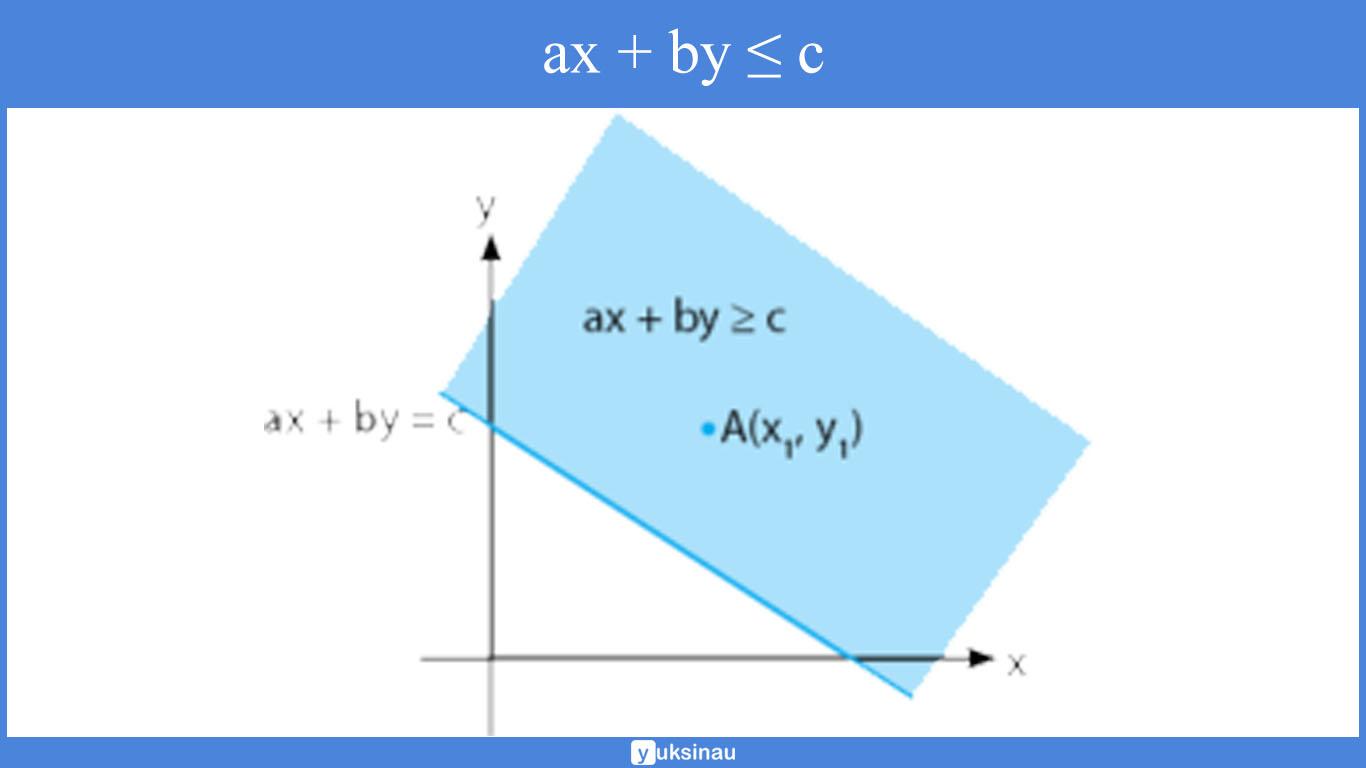
- Apabila ax1 + by1 ≥ c maka daerah yang memuat x1.y1 merupakan daerah penyelesaian dari pertidaksamaan ax + by ≥ c
Contoh cara untuk menentukan daerah himpunan penyelesaian dari sistem pertidaksamaan linear dua peubah.
Diberikan sistem pertidaksamaan linear seperi berikut ini.
x ≥ 0
y ≥ 0
x + y ≤ 7
x + 3y ≤ 15
Tentukan daerah yang memenuhi sistem pertidaksamaan linear di atas.
Jawab:
1. Daerah yang memenuhi pertidaksamaan x + y ≤ 7
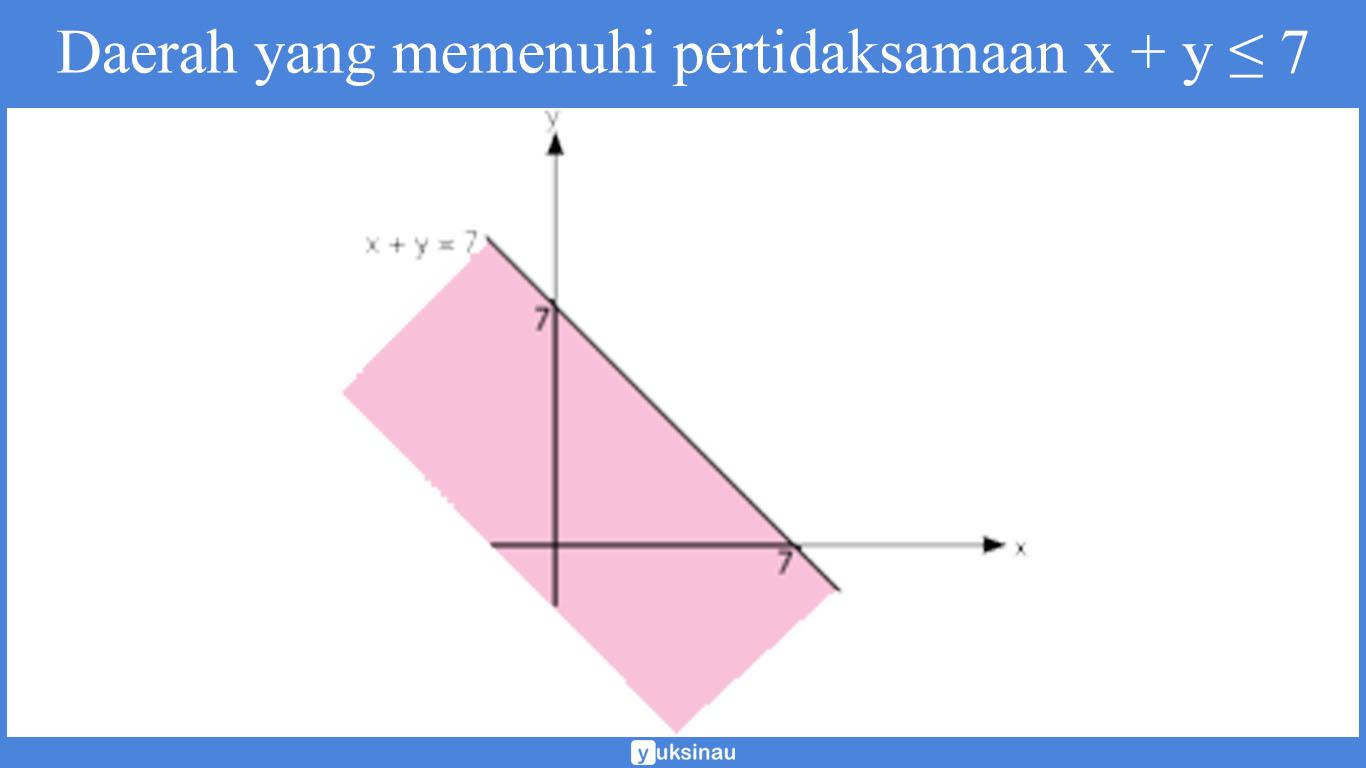
2. Daerah yang memenuhi pertidaksamaan x + 3y ≤ 15
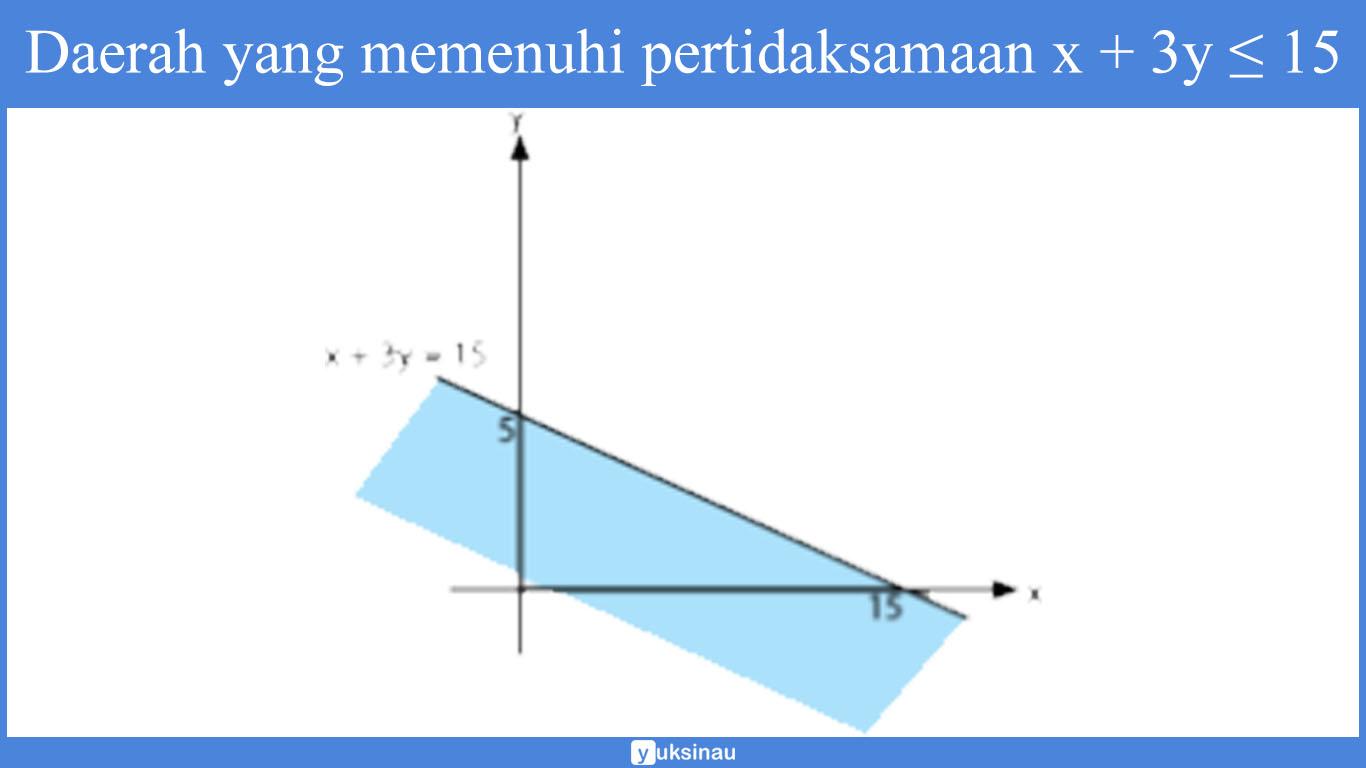
3. Daerah yang memenuhi gabungan dari empat sistem pertidaksamaan linear: x ≥ 0, y ≥ 0, x + y ≤ 7, x + 3y ≤ 15 yaitu:
Model Matematika
Model soal yang akan diberikan untuk program linear pada umumnya berupa soal cerita.
Supaya kalian bisa menyelesaikan soal cerita yang diberikan dengan mudah, kalian hanya perlu untuk merubahnya ke dalam model matematika.
Model matematika adalah sebuah cara untuk merubah permasalahan sehari-hari ke dalam bahasa matematika dalam bentuk persamaan, pertidaksamaan, dan juga fungsi.
Untuk penjelasan lebih lengkapnya, perhatikan penyelesaian pada persoalan berikut.
Contoh soal model matematika
Tentukan model matematika pada soal di bawah.
Suatu adonan roti basah dibuat dengan menggunakan bahan 2 kg tepung dan 1 kg gula. Sementara satu adonan roti kering dibuat dengan memakai 2 kg tepung dan 3 kg gula. Ibu mempunyai persediaan tepung sebanyak 6 kg dan gula sebanyak 5 kg. Apabila pada masing-maisng satu adonan kue basah bisa memberikan keuntungan Rp75.000,00 serta masing-masing adonan kue kering bisa memberikan untung Rp60.000,00. Berapakah banyak kombinasi adonan roti yang bisa dibikin untuk memperoleh keuntungan maksimal?
Jawab:
Misalnya:
x = adonan roti basah
y = adonan roti kering
Maka perhatikan tabel di bawah.
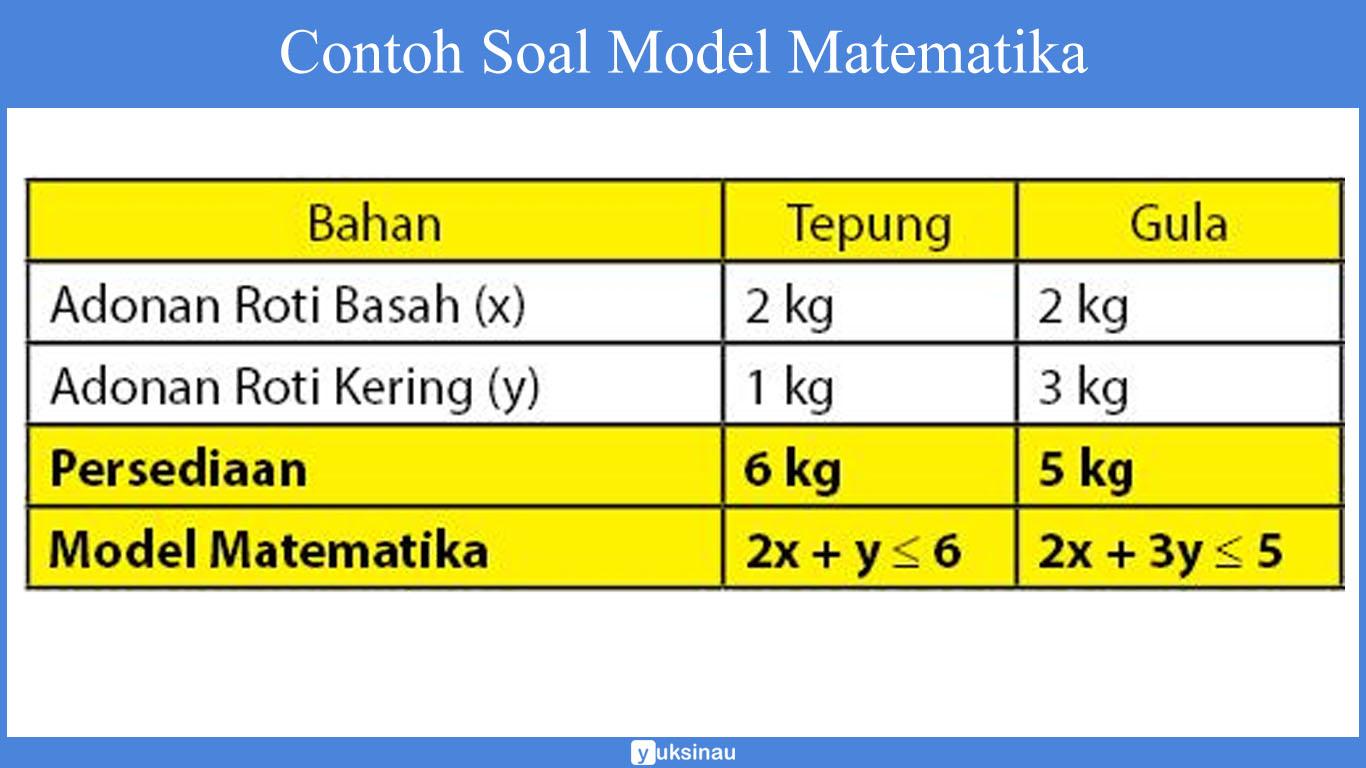
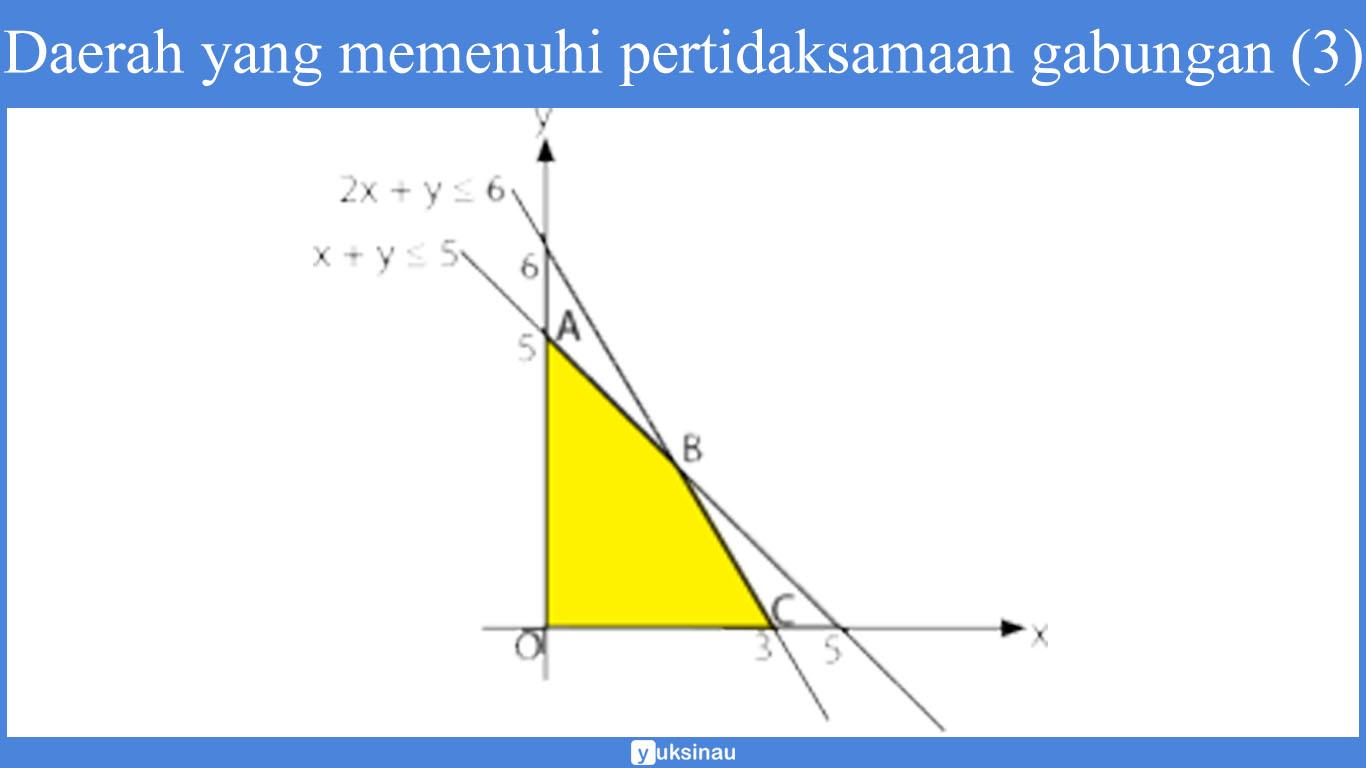
Sehingga akan didapatkan model matematika dari soal di atas sebagai berikut ini:
x ≥ 0
y ≥ 0
2x + y ≤ 6
x + y ≤ 5
Pembahasan yang diberikan tidak akan berhenti sampai di sini, belum sampai menentukan kombinasi jenis roti yang dibuat untuk memperoleh keuntungan maksimal.
Solusi selanjutnya yang akan kita lakukan adalah penjabaran materi di bawah ini.
Cara Menyelesaikan Masalah Program Linear
Cara menyelesaikan masalah program linear bisa disebut sebagai sebuah proses guna mencari nilai optimum dari sebuah pertidaksamaan.
Nilai itu bisa berwujud nilai maksimum atau minimum, tergantung dengan soal yang akan diberikan. Bentuk umum fungsi objektif dari sebuah model matematika yaitu f(x,y) = ax + by.
Adapun dua metode yang bisa kita pakai untuk mencari menentukan nilai optimum pada program linear.
Kedua metode tersebut adalah metode uji titik pojok dan garis selidik. Penjabaran secara lebih rincinya akan kalian liat pada ulasan di bawah.
Metode Uji Titik Pojok
Sesuai dengan namanya, metode uji titik pojok digunakan dengan cara menghitung nilai fungsi tujuan dari titik pojok yang didapatkan.
Titik pojok yang dimaksud di sini merupakan titik-titik koordinat yang membatasi daerah layak dari sebuah sistem pertidaksamaan linear.
Beberapa tahapan yang dilakukan untuk menentukan nilai optimum dengan menggunakan metode uji titik pojok yaitu sebagai berikut.
- Mencari berbagai garis dari sistem pertidaksamaan yang menjadi fungsi kendala dari persoalan yang diberikan.
- Mencari berbagai titik pojok yang merupakan koordinat pembatas daerah yang memenuhi fungsi kendala.
- Menghitung nilai optimum f(x,y) dari titik-titik pojok yang diperoleh.
- Memperoleh nilai maksimum atau minimum sesuai dengan permasalahan.
Untuk memperjelas pemahaman materi mengenai mencari nilai optimum dengan metode uji titik pojok. Maka akan kita selesaikan permasalah yang sudah dibahas sebagian pada bagian model matematika.
Berdasarkan pembahasan sebelumnya maka akan didapatkan sistem pertidaksamaan seperti di bawah ini.
x ≥ 0
y ≥ 0
2x + y ≤ 6
x + y ≤ 5
Lihat kembali pada soal yang telah kami berikan sebelumnya, fungsi tujuan bisa kita dapatkan dari kalimat berikut:
Apabila pada masing-maisng satu adonan kue basah bisa memberikan keuntungan Rp75.000,00 serta masing-masing adonan kue kering bisa memberikan untung Rp60.000,00.
Sehingga, fungsi tujuannya yaitu memaksimalkan f(x,y) = 75.000x + 60.000y.
Menggambar daerah yang memenuhi pada sistem pertidaksamaan di atas.
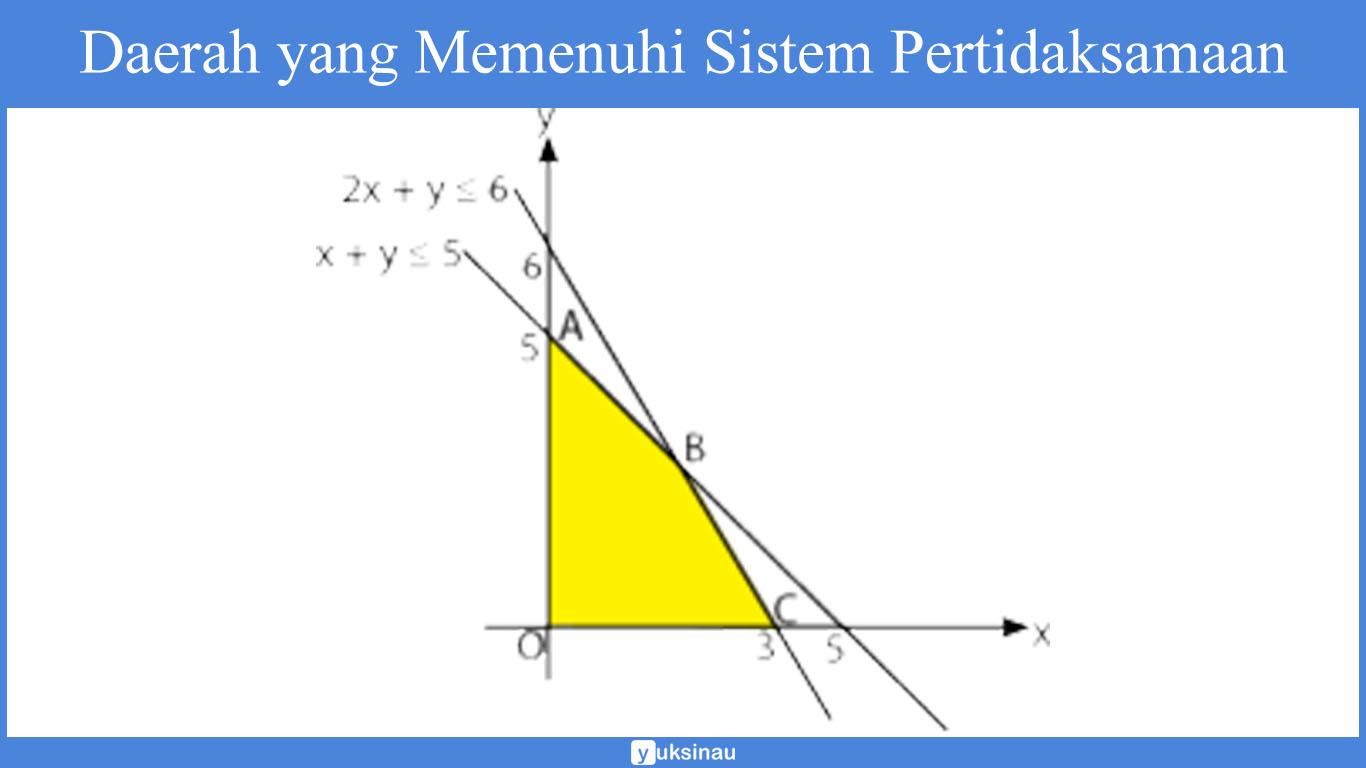
Menentukan titik koordinat yang menjadi titik pojok pembatas daerah layak dari permasalahan sistem pertidaksamaan.
Titik Koordinat O, A, dan juga C bisa kita peroleh dengan cara melihat gambar di atas. Yakni dengan melihat O(0,0), A(0, 5), dan juga C(3, 0).
Sementara untuk koordinat titik B bisa kita peroleh dengan memanfaatkan metode eliminasi.
Untuk mencari koordinat titik B maka caranya adalah sebagai berikut:
x + y = 5
2x + y = 6
________ –
-x = -1
x = -1/-1 = 1
Substitusi nilai x = 1 pada persamaan x + y = 5 untuk memperoleh nilai y.
x + y = 5
1 + y =5
y = 5 – 1 = 4
Koordinat titik B yaitu (1, 4)
Perhitungan nilai optimum:
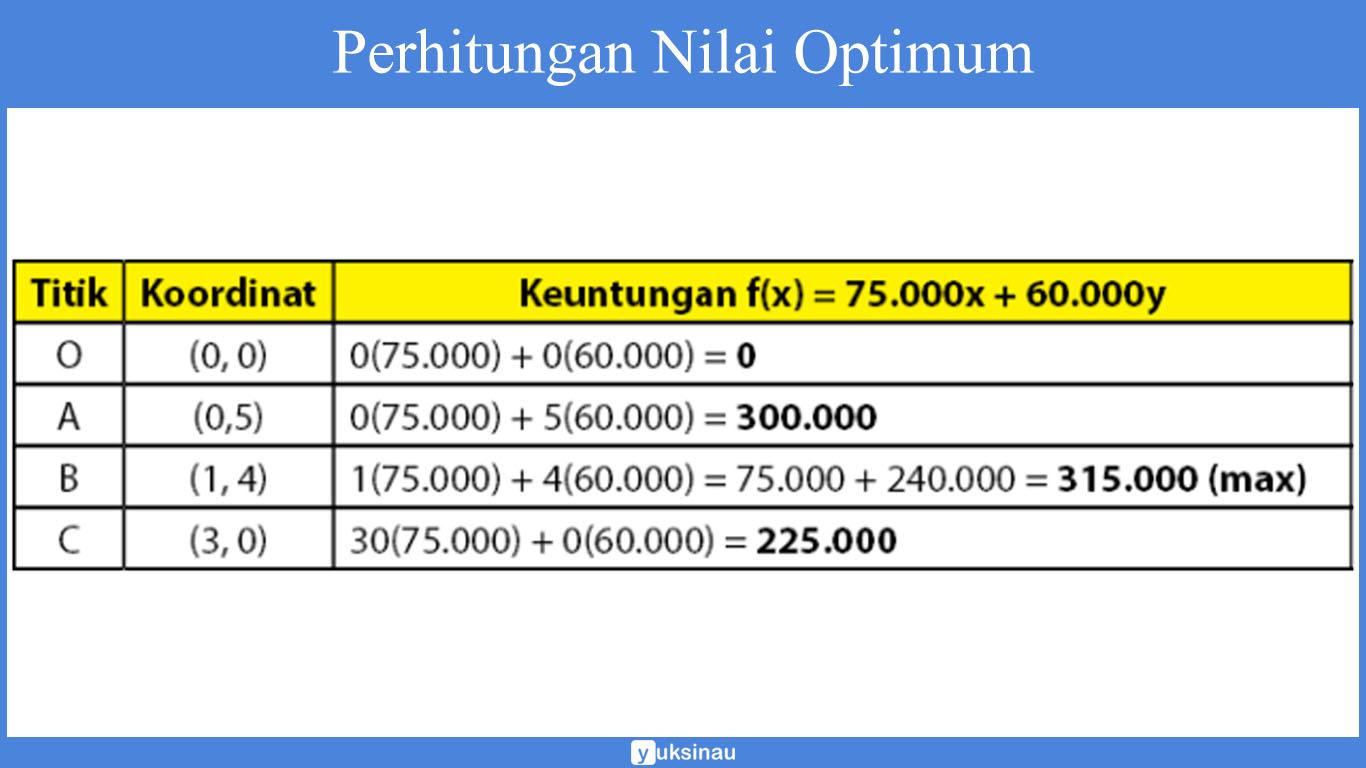
Sehingga, nilai keuntungan maksimum yang bisa didapatkan yaitu Rp315.000,00 dengan membuat 1 (satu) adonan roti basah dan juga 4 (empat) adonan roti kering.
Metode Garis Selidik
Selain metode uji titik pojok, cara lain yang bisa kita pakai untuk mengetahui nilai optimum yaitu metode garis selidik.
Pada metode garis selidik, cara yang bisa digunakan untuk mencari nilai optimum yang didapatkan dari persamaan fungsi objektif atau fungsi tujuannya.
Apabila fungsi tujuannya yaitu memaksimalkan. Maka nilai optimum didapatkan dari titik yang paling akhir menyentuh garis selidik yang digeser ke arah kanan mendekati daerah layak.
Sementara untuk nilai optimum dengan fungsi tujuan meminimumkan akan didapatkan dari titik koordinat yang pertama kali menyentuh geseran garis selidik yang digeser ke arah kiri mendekati daerah layak.
Hal itu juga berlaku untuk sebaliknya.
Berikut ini merupakan tahapan untuk menentukan nilai optimum dari fungsi objektif f(x,y) = ax + by dengan menggunakan metode garis selidik.
- Mencari daerah yang memenuhi sistem pertidaksamaan yang diberikan.
- Mencari persamaan garis selidik f(x,y) = ax + by = k, dengan k merupakan bilangan real.
- Apabila arah geser garis selidik ke arah kanan maka:
- Apabila titik (x1.y1) merupakan titik pada daerah penyelesaian yang pertama dilewati oleh garis selidik maka nilai minimum diwakili oleh titik tersebut.
- Apabila titik (x2.y2) merupakan titik pada daerah penyelesaian yang terakhir dilewati oleh garis selidik maka nilai maksimum diwakili oleh titik tersebut.
Geser garis selidik yang sudah dibikin pada langkah nomor 2 atau buatlah garis-garis lain yang sejajar dengan garis selidik yang sudah dibikin pada arah daerah layak.
- Apabila arah geser garis selidik ke kiri, maka:
- Apabila titik (x1.y1) merupakan titik pada daerah penyelesaian yang pertama dilewati oleh garis selidik maka nilai maksimum akan diwakili oleh titik tersebut.
- apabila titik (x2.y2) merurpakan titik pada daerah penyelesaian yang terakhir dilewati oleh garis selidik maka nilai minimum diwakili oleh titik tersebut.
Untuk lebih jelasnya mengenai materi mencari nilai optimum dengan metode garis selidik, maka kali ini kita akan memakainya untuk menyelesaikan permasalah yang sudah kita bahas pada bagian model matematika.
Berdasarkan pembahasan sebelumnya maka didapatkan sistem pertidaksamaan seperti berikut ini:
x ≥ 0
y ≥ 0
2x + y ≤ 6
x + y ≤ 5
Lihat kembali pada soal yang telah kami berikan sebelumnya, fungsi tujuan bisa kita dapatkan dari kalimat berikut:
Apabila pada masing-maisng satu adonan kue basah bisa memberikan keuntungan Rp75.000,00 serta masing-masing adonan kue kering bisa memberikan untung Rp60.000,00.
Sehingga, fungsi tujuannya yaitu memaksimalkan f(x,y) = 75.000x + 60.000y.
Persamaan garis selidik (ambil nilai k = 600.000):
f(x,y) = k
75.000x + 60.000y = 600.000
5x + 4y = 40
Menggambar daerah yang memenuhi sistem pertidaksamaan di atas serta garis selidiknya.
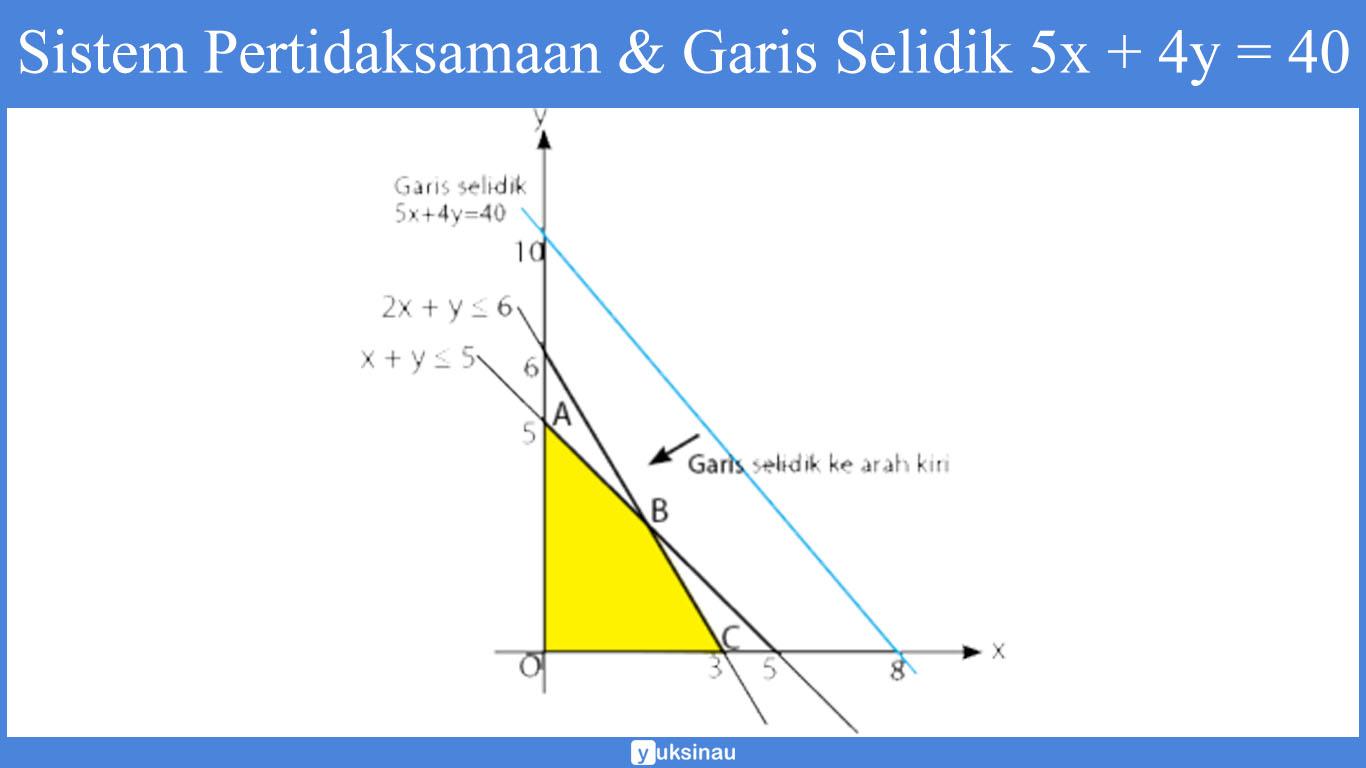
Nilai maksimum akan diwakili oleh titik B (titik yang pertama kali menyentuh garis selidik yang digeser ke arah kiri).
Mencari koordinat titik B dengan cara seperti berikut:
x + y = 5
2x + y = 6
________ –
-x = -1
x = -1/-1 = 1
Substitusi nilai x = 1 pada persamaan x + y = 5 untuk memperoleh nilai y.
x + y = 5
1 + y =5
y = 5 – 1 = 4
Koordinat titik B yaitu (1, 4)
Substitusi koordinat titik B(1,4) pada persamaan f(x,y) = 75.000x + 60.000y.
f(x,y) = 75.000x + 60.000y
f(x,y) = 75.000(1) + 60.000y(4)
f(x,y) = 75.000 +240.000
f(x,y) = 315.000
Sehingga, nilai keuntungan maksimum yang bisa didapatkan yakni Rp315.000,00 dengan membuat 1 (satu) adonan roti basah serta 4 (empat) adonan roti kering.
Garis Selidik (Tambahan)
Garis selidik didapatkan dari fungsi objektif f(x, y) = ax + by di mana garis selidiknya yaitu ax + by = Z.
Nilai Z akan diberikan sembarang nilai. Garis ini dibikin sesudah grafik himpunan penyelesaian pertidaksamaan selesai dibikin.
Garis selidik awal dibikin pada area himpunan penyelesaian awal. Lalu dibikin berbagai garis yang sejajar dengan garis selidik awal.
Berikut adalah panduan untuk memudahkan penyelidikian nilai fungsi optimum:
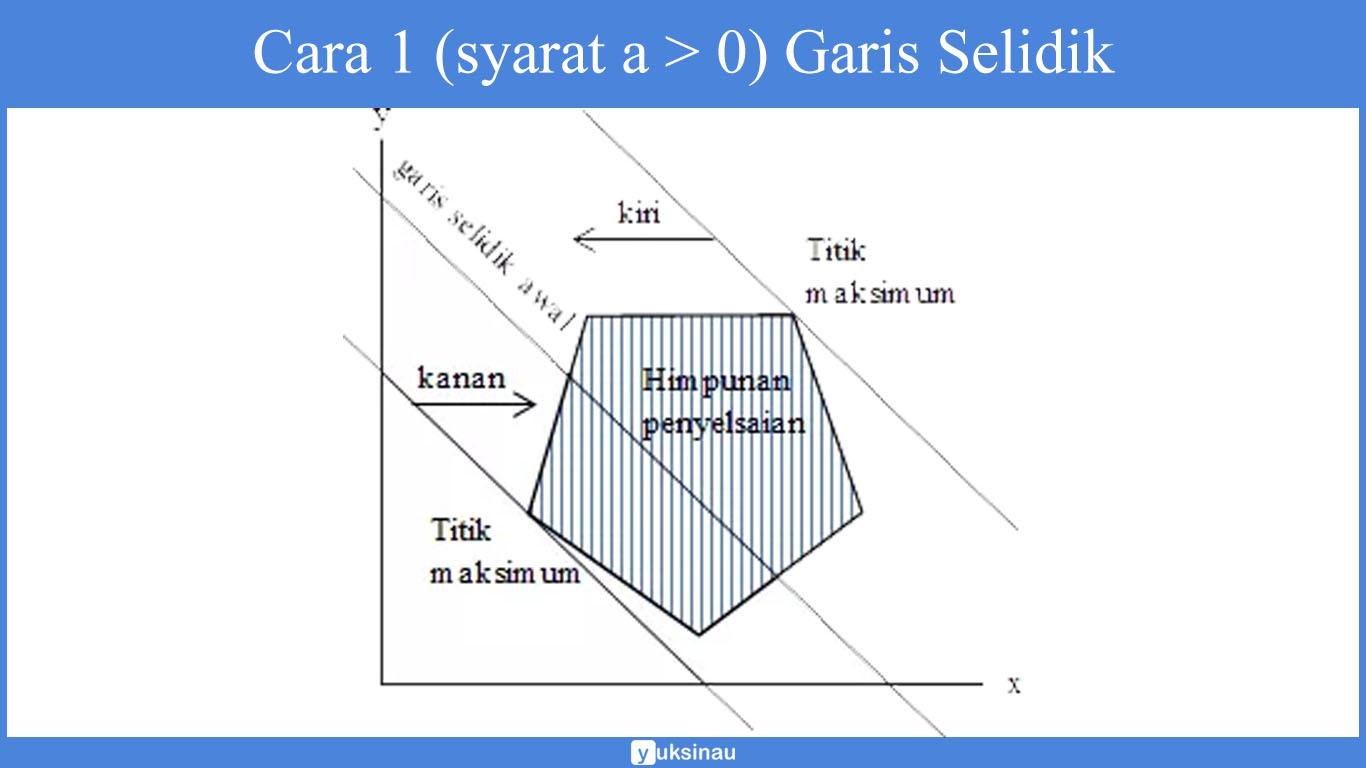
Cara 1 (syarat a > 0)
- Apabila maksimum, maka dibikin garis yang sejajar garis selidik awal sehingga akan membuat himpunan penyelesaian terletak di kiri garis tersebut. Titik yang dilewati oleh garis tersebut merupakan titik maksimum.
- Apabila minimum, maka dibikin garis yang sejajar garis selidik awal sehingga akan membuat himpunan penyelesaian terletak pada kanan garis tersebut. Titik yang dilewati garis tersebut merupakan titik minimum.
Cara 2 (syarat b > 0)
- Apabila maksimum, maka dibikin garis yang sejajar dengan garis selidik awal sehingga akan membuat himpunan penyelesaian terletak pada bawah garis tersebut. Titik yang dilewati garis tersebut merupakan titik maksimum.
- Apabila minimum, maka dibikin garis yang sejajar garis selidik awal sehingga akan membuat himpunan penyelesaian terletak pada atas garis tersebut. Titik yang dilewati garis tersebut merupakan titik minimum.
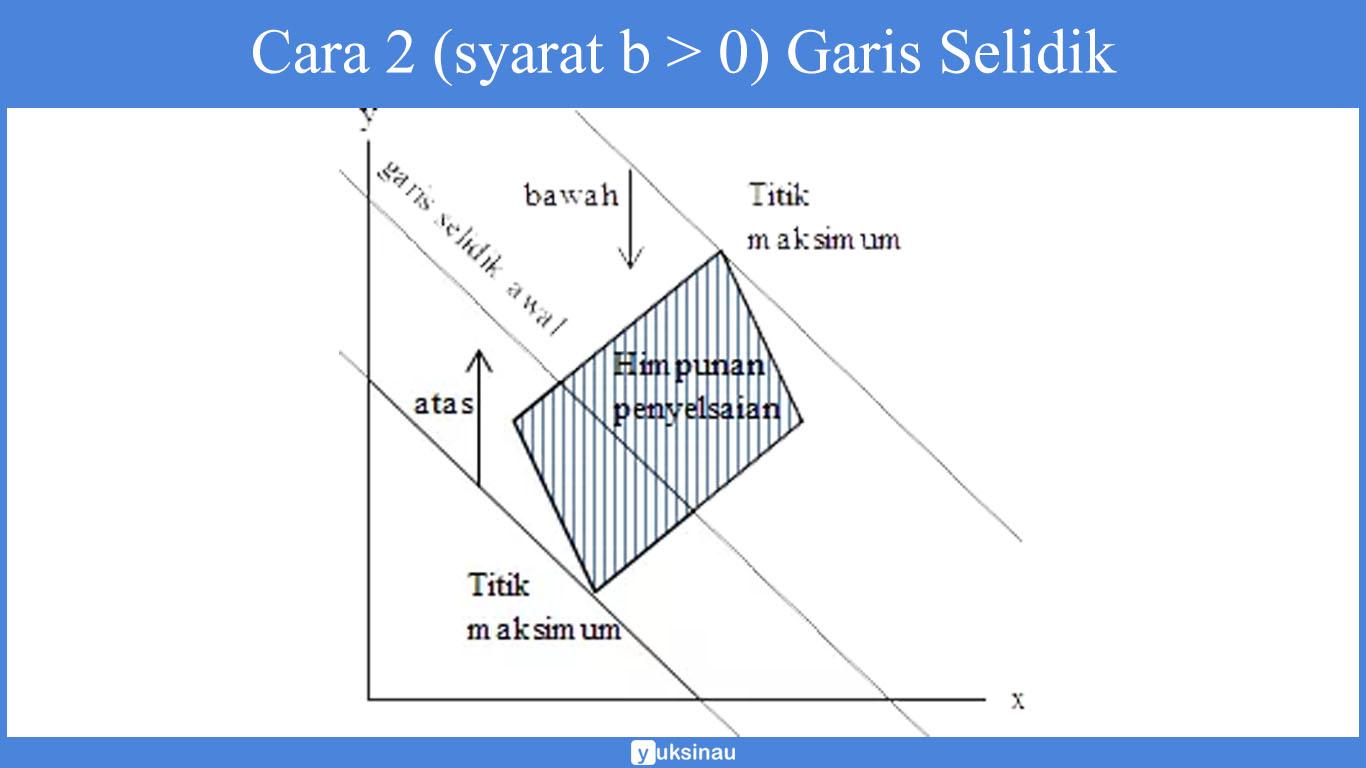
Untuk nilai a < 0 dan b < 0 berlaku kebalikan dari kedua cara yang telah diuraikan di atas.
Membandingkan Nilai Fungsi Tiap Titik Ekstrim
Menyelidiki nilai optimum dari fungsi objektif juga bisa kita lakukan dengan cara mencari terlebih dahulu titik-titik potong dari berbagai garis batas yang ada.
Titik-titip potong tersebut adalah nilai ekstrim yang berpotensi mempunyai nilai maksimum pada salah satu titiknya.
Berdasarkan dari beberapa titik tersebut akan ditentukan nilai dari tiap-tiap fungsinya, lalu dibandingkan. Nilai terbesar adalah nilai maksimum serta nilai terkecil adalah nilai minimum.
Bagian terakhir yakni tentang contoh soal sekaligus pembahasan program linear matematika SMA yang akan diberikan dalam beberapa contoh soal seperti di bawah ini:
Contoh Soal dan Pembahasan
Soal 1. (Soal Ujian Nasional)
Luas daerah parkir . Luas rata-rata sebuah mobil
dan luas rata-rata bus
. Daerah parkir tersebut dapat memuat paling banyak 30 kendaraan roda empat (mobil dan bus). Jika tarif parkir mobil Rp2000,00 dan tarif parkir bus Rp5000,00 maka pendapatan terbesar yang dapat diperoleh adalah ….
A. Rp40.000,00
B. Rp50.000,00
C. Rp60.000,00
D. Rp75.000,00
E. Rp90.000,00
Jawab:
Misalkan bahwa:
x = banyak mobil
y = banyak bus
Perhatikan tabel di bawah ini!
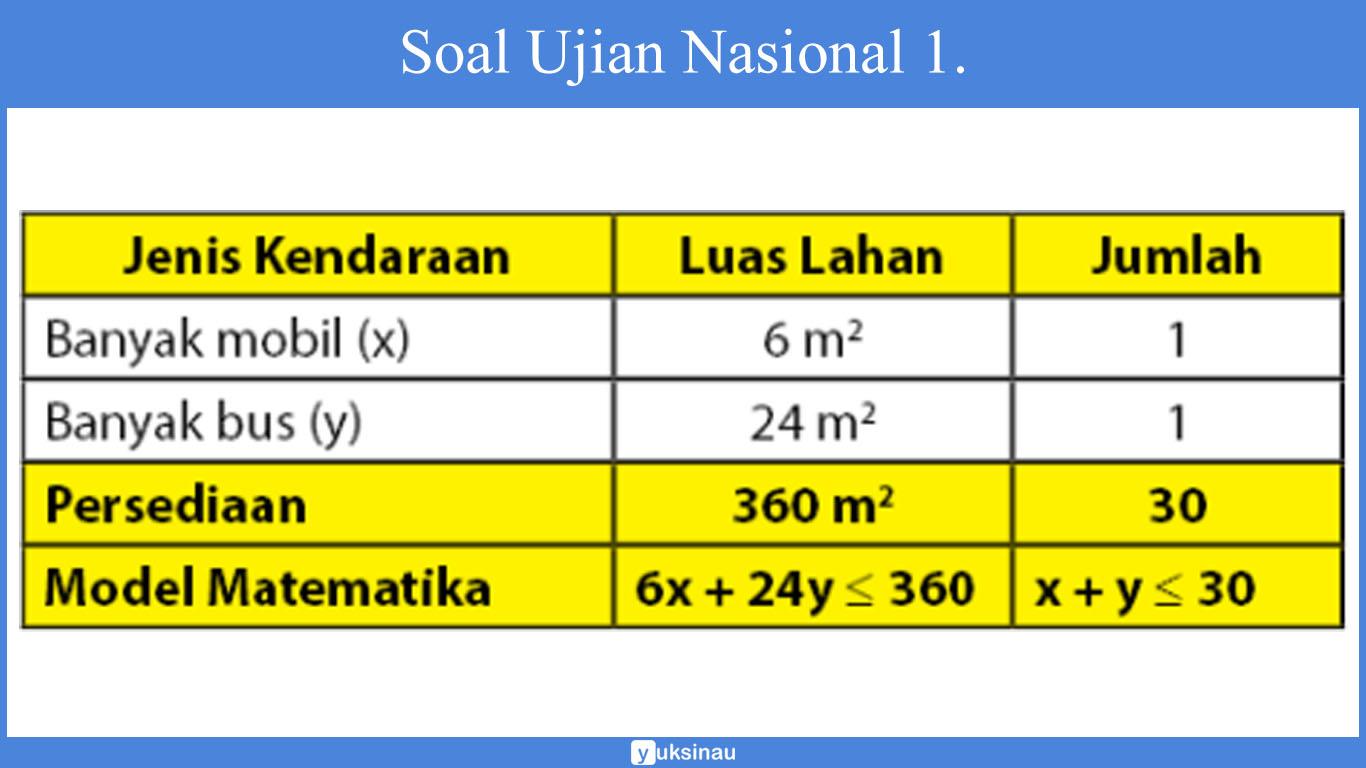
Maka akan didapatkan dua persamaan berikut ini:
x + y ≤ 30
6x + 24y ≤ 360 → x + 4y ≤ 60
Menentukan daerah yang memenuhi pertidaksamaannya yakni:
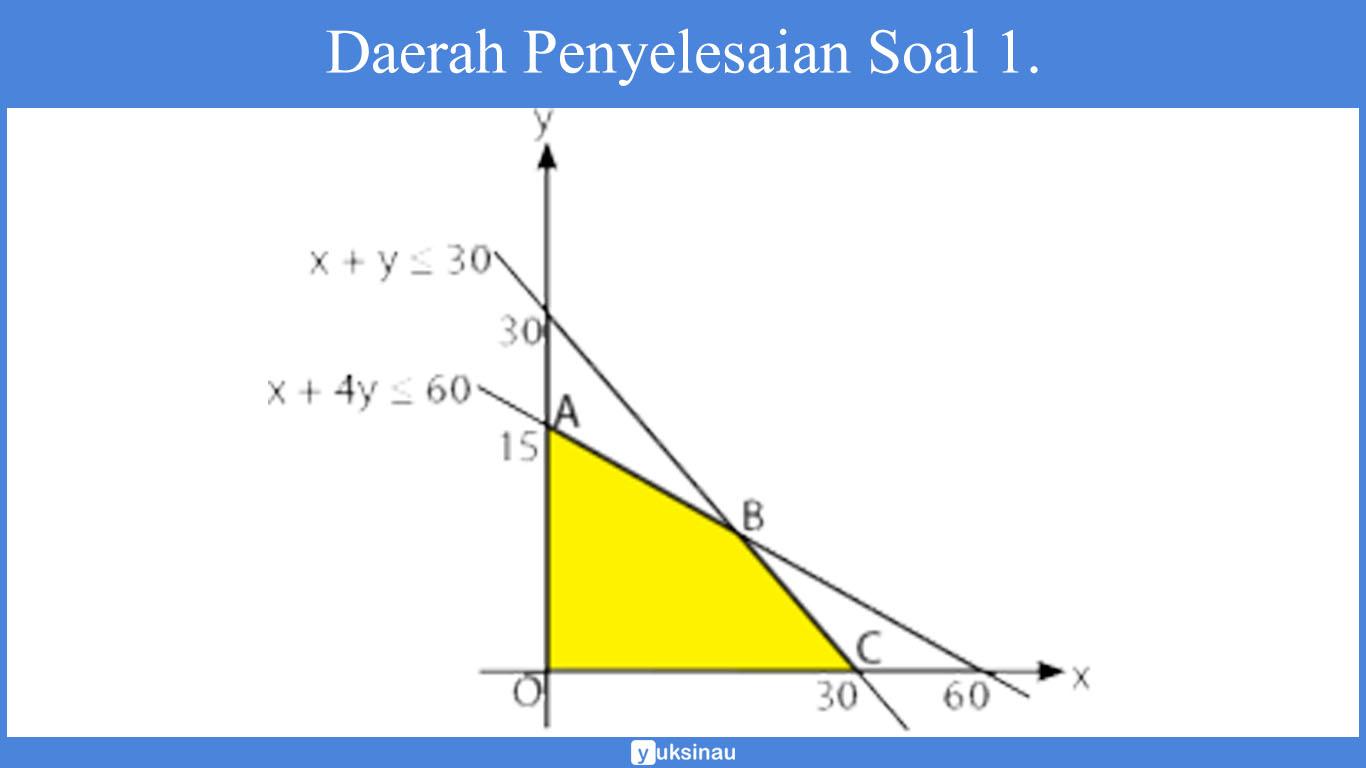
Akan ditentukan nilai maksimum dengan metode titik sudut sebagai berikut.
Titik koordinat O, A, dan juga C bisa didapatkan dengan melihat gambar di atas. Yakni O(0,0), A(0, 15), serta C(30,0). Untuk koordinat B bisa kita dapatkan dengan memakai metode eliminasi dan substitusi.
x + y = 30
x + 4y = 60
________ –
-3y = -30
x = -30/-3 = 3
Substitusi nilai y = 10 pada persamaan x + y = 30 untuk memperoleh nilai x.
x + y = 30
x + 10 = 30
x = 30 – 10 = 20
Koordinat titik B yaitu (20, 10).
Perhitungan keuntungan maksimal yang bisa didapatkan adalah:
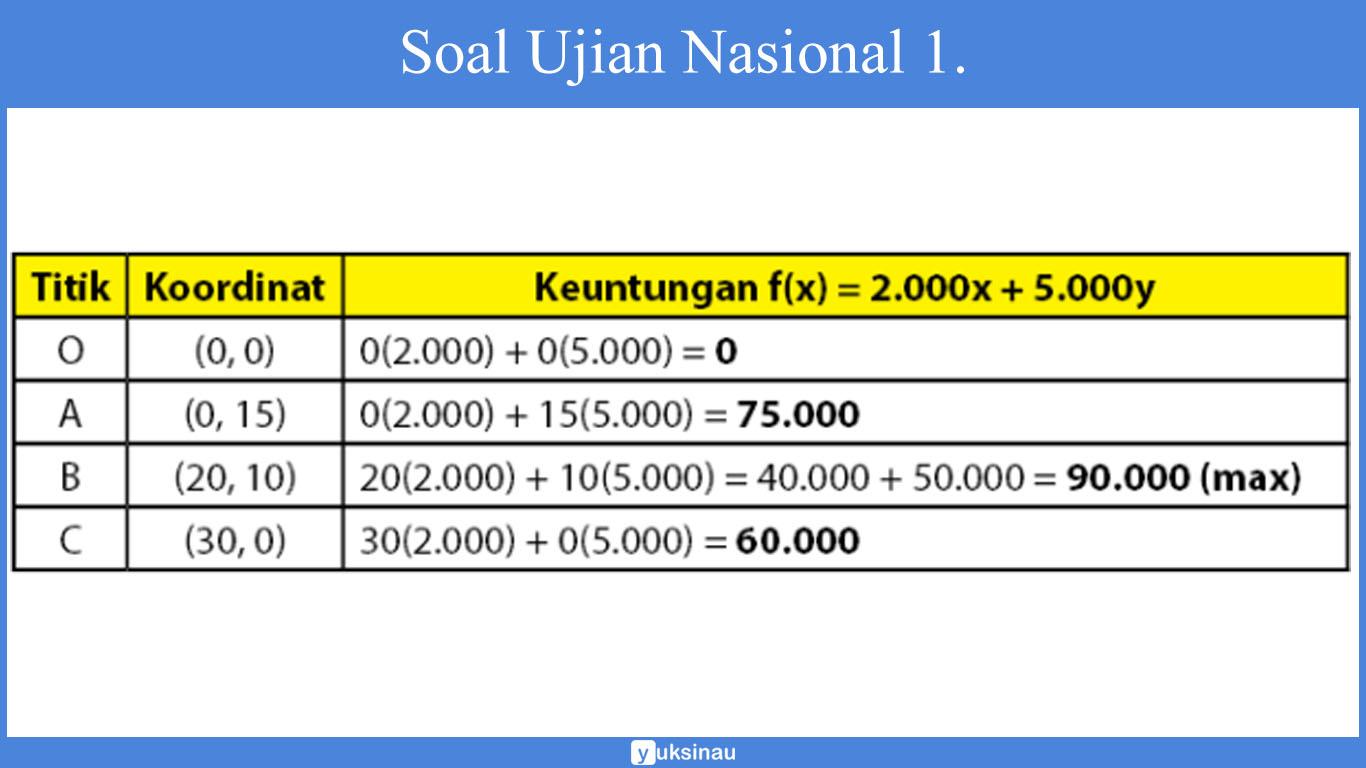
Jawaban: E
Soal 2.
Biaya produksi pada sebuah buah payung jenis A sebesar Rp20.000,00 per buah. Sementara untuk biaya satu buah produksi payung jenis B sebesar Rp30.000,00.
Seorang pengusaha akan membuat payung A dengan jumlah tidak kurang dari 40 buah. Sementara banyaknya payung jenis B yang akan diproduksi minimal yaitu dari 50 buah. Jumlah maksimal produksi kedua payung tersebut berjumlah 100 buah. Biaya minimum yang dikeluarkan untuk melakukan produksi kedua payung sesuai dengan ketentuan tersebut yaitu ….
A. Rp2.000.000,00
B. Rp2.300.000,00
C. Rp2.200.000,00
D. Rp2.100.000,00
E. Rp2.000.000,00
Jawab:
Misalnya:
x = banyak payung A
y = banyak payung B
Model matematika dari permasalahan tersebut yaitu:
Fungsi tujuan: meminimumkan
f(x,y) = 20.000x + 30.000y
Fungsi kendala:
x ≥ 40
y ≥ 50
x + y ≤ 100
Daerah penyelesaian yang memenuhi permasalahan yaitu:
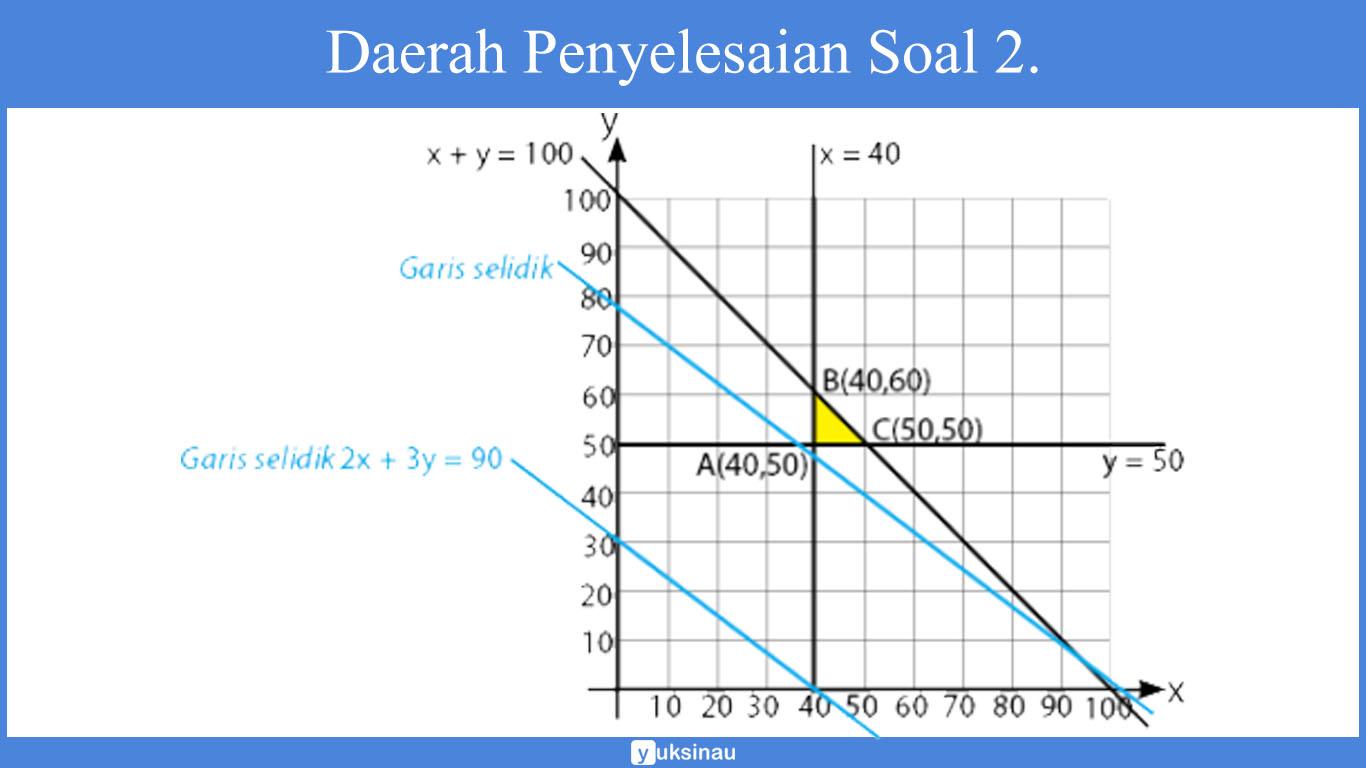
Nilai minimim akan didapatkan dengan melewati titik koordinat yang dilalui oleh garis selidik yang pertama kali. Yakni pada titik A(40, 50). Sehingga, biaya produksi minimumnya yaitu:
f(40,50) = 20.000(40) + 30.000(50)
f(40,50) = 800.000 + 1.500.000
f(40,50) = 2.300.000
Jawaban: B
Soal 3.
Tentukan nilai minimum f(x, y) = 9x + y pada daerah yang dibatasi oleh 2 ≤ x ≤ 6, dan 0 ≤ y ≤ 8 serta x + y ≤ 7.
Jawab:
- Tahap 1 menggambar grafiknya
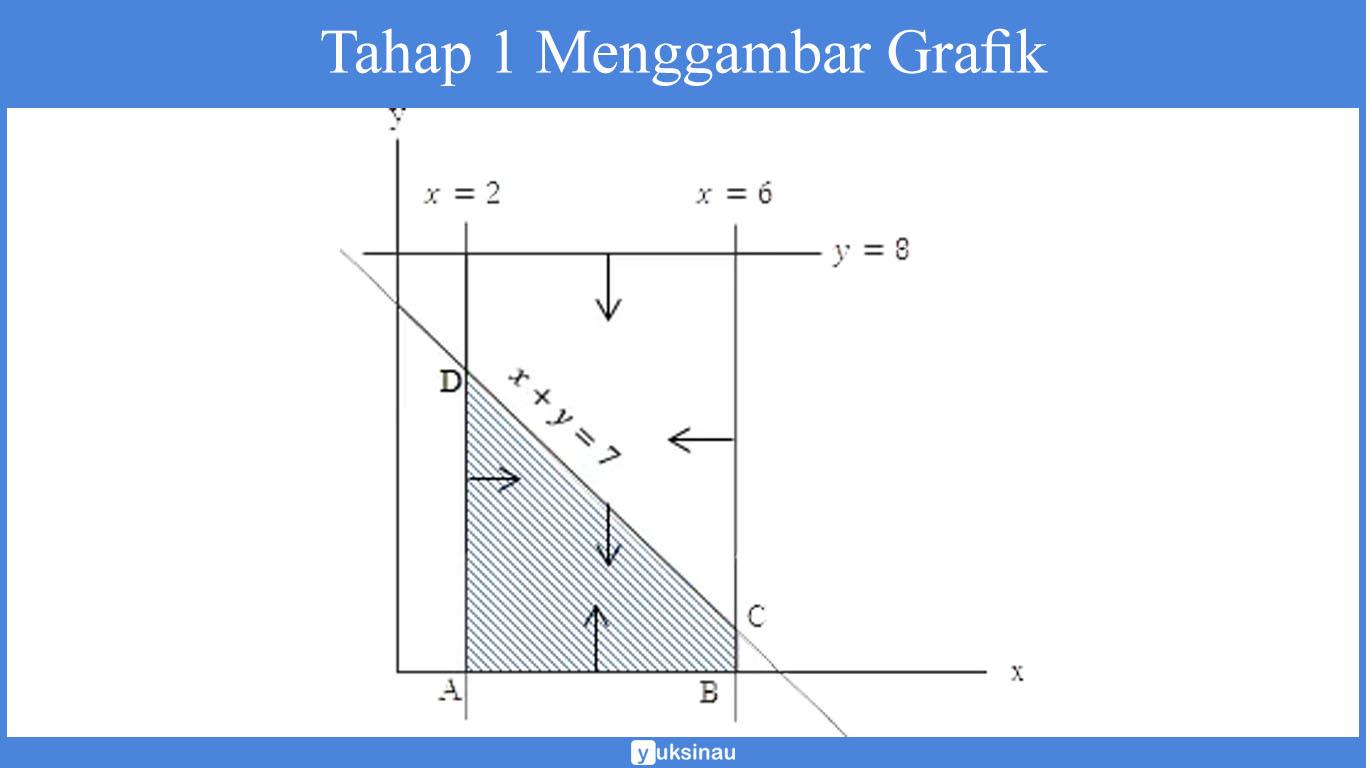
- Tahap 2 menentukan titik ekstrim
Dari gambar, terdapat 4 titik ekstrim, yakni: A, B, C, D serta himpunan penyelesaiannya terdapat pada area yang diarsir.
- Tahap 3 menyelidiki nilai optimum
Dari grafik diketahui titik A dan B mempunyai y = 0, sehingga kemungkinan menjadi nilai minimum. Kedua titik disubstitusikan ke dalam f(x, y) = 9x + y untuk dibandingkan.

Dengan membandingkan, disimpulkan titik A mempunyai nilai minimum 18.
Soal 4.
Tentukan dimana nilai maksimum fungsi f(x, y) = 4x + 5y yang akan diperoleh pada pada grafik ini!

Titik ekstrim yang ada di gambar antara lain:
- A tidak mungkin maksimum sebab titik paling kiri.
- B(3, 6)
- C(8, 2)
- D(8, 0)
Nilai tiap titik ekstrim merupakan:
- B(3, 6) → f(3, 6) = 4(3) + 5(6) = 42
- C(8, 2) → f(8, 2) = 4(8) + 5(2) = 42
- D(8, 0)→ f(8, 0) = 4(8) + 5(0) = 32
Sehingga nilai maksimum ada pada titik yang melewati garis BC yaitu 42.
Demikianlah ulasan singkat kali ini yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.
yang kue kering di soal sama tabel 2x + 3y ≤ 5 lah kok pas penyelesaiannya jadi x + y ≤ 5