Taukah kamu apa itu pertidaksamaan linear? Pertidaksamaan merupakan suatu kalimat terbuka yang menyatakan hubungan dua hal yang tidak memiliki kesamaan atau tidak sama dengan, serta memakai berbagai tanda seperti:
- < (kurang dari)
- ≤ (kurang dari atau sama dengan
- > (lebih dari)
- ≥ (lebih dari atau sama dengan)
Apabila terdapat pertidaksamaan x < a maka niai x yang memenuhi merupakan lebih kecil dari a serta di dalam garis bilangan akan dilukis seperti:

Apabila terdapat pertidaksamaan matemati x ≥ a maka nilai x yang memenuhi merupakan lebih besar dari a serta di dalam garis bilangan akan dilukis seperti:

Daftar Isi
Sifat Pertidaksamaan Linear
1. Tanda pertidaksamaan tidak akan berubah apabila kalian menambahkan maupun mengurangkan suatu pertidaksamaan dengan bilangan atau suatu ekspresi matemtaika tertentu.
Apabila a > b maka:
a+c > b+c ; a-c > b-c
Apabila a<b maka:
a+c < b+c ; a-c < b-c
Sebagai contoh:
x + 6 > 8 ⇒ x+6-6 > 8-6 ⇒ x > 2
2. Tanda pertidaksamaan tidak akan berubah apabila kalian mengalikan maupun membaginya dengan bilangan POSITIF
Apabila a > b dan c > 0 maka:
ac > bc dan a/c > b/c
Sebagai contoh:
4x ≥ 12.
Apabila kalian membagi pada setiap ruas dengan angka 4 (positif), maka:
4x/4 ≥ 12/ 4 ⇒ x ≥ 3
3. Tanda pertidaksamaan akan berbalik apabila dikalikan maupun dibagi dengan suatu bilangan NEGATIF.
Apabila a > b dan c < 0 maka:
ac < bc dan a/c < b/c (amati jika tanda berbalik)
Banyak kalian hitung yang mungkin lupa dengan keharusan membalik tanda.
Seperti contoh berikut ini:
-3x ≥ 9 untuk menyelesaikan pertidaksamaan tersebut kalian harus membagi terlebih dahulu pada masing-masing ruas kanan dan kiri dengan -3.
Atau dengan sebutan lain mengalikan pada masing-masing ruas dengan -1/3. Sebab dikali dengan bilangan negatif maka tanda wajib akan berbalik.
-3x ≥ 9 ⇒ -3x/-3 ≤ 9/-3 ⇒ x ≤ -3 (amati tanda berbalik)
4. Eksponen (Pemangkatan) Pertidaksamaan
Terdaat hal unik dari pemangkatan pertidaksamaan matematika, di mana tanda pertidaksamaan berbalik yang bergantung dari ganjil atau genap pangkatnya.
Apabila a > b > 0 maka:
a2 > b2 > 0
a3 > b3 > 0
a4 > b4 > 0
a5 > b5 > 0
begitu seterusnya. Secara umum an > bn ; a merupakan bilangan asli
Apabila a < b < 0 maka:
a2 > b2 > 0
a3 < b3 < 0
a4 > b4 > 0
a5 < b5 < 0
begitu seterusnya. Secara umum an > bn, apabila n genap dan an < bn apabila n ganjil
Sebagai contoh:
x < -2 apabila kalian pangkatkan dua didapat x2 > (-2)2 (tanda akan berubah apabila n genap akan selalu an > bn) dan logikanya masuk apabila x saja kurang dari -2 (-3, -4, -5, dan seterusnya) pasti x2 akan selalu menghasilkan lebih dari 4, -32 = 9; -42 = 16, dan seterusnya.
Rangkuman Sifat Pertidaksamaan:
- Apabila a serta b bilangan real maka akan berlaku a > b atau a = b atau a < b
- Apabila a > b serta b > c maka a > c
- Apabila a > b maka a + c
- Apabila a > b serta c > 0 maka ac > bc serta a/c > b/c
- Apabila a > b serta c < 0 maka ac < bc serta a/c < b/c
- Apabila m genap serta a > b maka:
- a– > b– ,untuk a > 0 dan juga b > 0
- a– < b– ,untuk a < 0 dan juga b < 0
- Apabila n ganjil serta a > b maka an > bn
- Apabila a > b maka:
- 1/a > 1/b untuk a dan juga b bertanda sama.
- 1/a < 1/b untuk a dan juga b berbeda tanda.
Interval Bilangan
Interval bilangan merupakan cara penyelesaian dari suatu pertidaksamaan, diantaranya yaitu perhatikan tabel di bawah ini:

Definit
Jenis Definit
1. Definit Positif
Bentuk dari definit positif yaitu:
ax2 + bx + c = 0
Disebut sebagai definit positif apabila a > 0 dan D < 0. Apabila pertidakasamaan ax2 + bx + c > 0 dalam keadaan definit positif, sehingga penyelesaiannya merupakan seluruh x Î R.
2. Definit Negatif
Bentuk dari definit negatif yaitu:
ax2 + bx + c = 0
Disebut sebagai definit negatif apabilaa= a < 0 dan D < 0. Apabila pertidakasamaan ax2 + bx + c < 0 dalam keadaan definit negatif, maka penyelesaiannya merupakan seluruh x Î R.
Sifat Definit
1. Untuk f(x) definit positif serta g(x) sembarang, berikut ketentuannya:
- f(x)g(x) > 0 → g(x) > 0
- f(x)g(x) < 0 → g(x) < 0
- f(x)/ g(x) > 0 → g(x) > 0
- f(x)/ g(x) < 0 → g(x) < 0
2. Untuk f(x) definit negatif serta g(x) sembarang, berikut ketentuannya:
- f(x)g(x) > 0 → g(x) < 0
- f(x)g(x) < 0 → g(x) > 0
- f(x)/ g(x) > 0 → g(x) < 0
- f(x)/ g(x) < 0 → g(x) > 0
Jenis Pertidaksamaan
Berikut akan kami berikan beberapa jenis dari pertidaksamaan, simak baik-baik ya.
1. Pertidaksamaan linear
Pertidaksamaan linear merupakan pertidaksamaan di mana salah satu atau kedua ruasnya mengandung bentuk linier di dalam x.
Dan disini akan kami berikan pertidaksamaan dari satu variabel dan dua variabel, diantaranya yaitu:
Pertidaksamaan Linear Satu Variabel (PtLSV)
Pertidaksamaan Linear Satu Variabel- Pertidaksamaan linear satu variabel merupakan suatu kalimat terbuka yang hanya mempunyai satu variabel dan berderajat satu serta memuat hubungan (<,> > atau < ).
Sebagai contohnya, lihat beberapa kalimat seperti di bawah ini:
- X > 9
- 3x – 3 < 8
- 3b > b + 6
- 5n – 3 < 3n + 2
Beberapa kalimat terbuka di atas menggunakan tanda hubung seperti <, >, > atau <. Yang menandakan kalimat tersebut merupakan pertidaksamaan.
Masing-masing pertidaksamaan itu hanya memiliki satu variabel, yakni x, a dan n. Pertidaksamaan tersebut disebut sebagai pertidaksamaan satu variabel. Peubah (variabel) pertidaksamaan di atas berpangkat satu atau juga disebut sebagai berderajat satu menjadi dinamakan pertidaksamaan linear.
Pertidaksamaan linear satu variabel merupakan kalimat terbuka yang hanya mempunyai satu variabel dan berderajat satu serta terdapat hubungan (<, >, ³atau £ ).
Bentuk umum dari PtLSV dalam variabel dapat dinyatakan seperti di bawah ini:
ax + b < 0, ax + b > 0, atau ax + b > 0, atau ax + b < 0,dengan a < 0, a serta b merupakan bilangan nyata (real).
Dibawah ini terdapat beberapa contoh dari PtLSV dengan menggunakan variabel x, antara laing:
- 3x – 2 < 0
- 3x – 2 < 0
- 5x – 1 > 8
- 3x + 1 > 2x – 4
- 10 < 2(x + 1)
Sifat Pertidaksamaan Linear Satu Variabel
Sama halnya dengan yang ada dalam persamaan linear satu variabel, dalam mencari penyelesaian pertidaksamaan linear satu variabel bisa dilakukan dengan menggunakan cara subtitusi.
Namun, kalian juga dapat melakukannya dengan cara mengurangkan, menjumlahkan, mengkali, ataupun membagi kedua ruas pertidaksamaan dengan bilangan yang sama.
Pertidaksamaan dalam matematika merupakan kalimat atau pernyataan matematika yang menunjukkan perbandingan ukuran dua objek atau lebih.
Seperti yang ada pada A < B pertidaksamaan linear satu variabel x dan C merupakan konstanta tidak nol.
Pertidaksamaan A < B ekuivalen dengan:
- A + C < B + C
- A – C < B – C
- A x C < B x C, bila C > 0 untuk seluruh x
- A x C > B x C, bila C < 0 untuk seluruh x
- A/C < B/C, bila C > 0 untuk seluruh x
- A/C > B/C, bila C < 0 untuk seluruh x
Perlu kalian catat, beberapa sifat di atas juga berlaku untuk lambang “>” atau “<”.
Contoh Soal PtLSV dan Cara Penyelesaiannya
Di bawah ini akan kami berikan contoh soal sekaligus cara penyeleaiannya dan juga jawaban dari soal pertidaksamaan linear satu variabel. Berikut ulasan selengkapnya.
1. Penjumlahan dan Pengurangan Pertidaksamaan Linear Satu Variabel (PtLSV)
Silakan perhatikan pertidaksamaan yang ada di bawah ini:
x + 3 < 8, dengan x variabel dari bilangan bulat.
Untuk:
x = 1, jadi 1 + 3 < 8, bernilai benar
x = 2, jadi 2 + 3 < 8, bernilai benar
x = 3, jadi 3 + 3 < 8, bernilai benar
x = 4, jadi 4 + 3 < 8, bernilai salah
Pengganti x merupakan 1,2, dan 3 sehingga pertidaksamaan x + 3 < 8 merupakan benar dinamakan penyelesaian dari pertidaksamaan tersebut.
2. Perkalian atau pembagian Pertidaksamaan Linear Satu Variabel (PtLSV)
Perhatikan pertidaksamaan dibawah ini:

Untuk bilangan x asli kurang dari 10 maka penyelesaiannya yakni x = 7, x = 8, atau x = 9
Berdasarkan uraian di atas, bisa kita tarik kesimpulan bahwa:
“Setiap pertidaksamaan tetap ekuivalen, dengan tanda ketidaksamaan tidak berubah, walaupun kedua ruas dikalikan dengan bilangan positif yang sama”
Contoh Soal:

Saat ini perhatikan pertidaksamaan berikut ini:
a. –x > – 5, dengan x adalah bilangan asli kurang dari 8. Pengganti x yang memenuhi yaitu x = 1, x = 2, x = 3 atau x = 4.
Cara lain untuk menyelesaikan soal pertidaksamaan di atas yakni dengan cara mengalikan kedua ruasnya dengan bilangan negatif yang sama.
* –x > –5
–1(–x) > – 1(–5), (kedua ruas dikalikan dengan –1 dan tanda pertidaksamaan tetap)
x > 5
Penyelesaiannya yaitu dengan x = 6 atau x = 7.
* –x > –5
–1(–x) < –1(–5), (kedua ruas dikalikan dengan –1 serta tanda pertidaksamaan berubah dari > menjadi <)
x < 5
Penyelesaiannya yakni x = 1, x = 2, x = 3, atau x = 4.
Berdasarkan penyelesaian tersebut ternyata, pertidaksamaan yang mempunyai penyelesaian sama adalah:
–x > –5 dan –1(–x) < –1(–5)
sehingga, –x > –5 <=> –1(–x) < –1(–5)
b. –4x <–8, dengan x bilangan asli kurang dari 4. Pengganti x yang memenuhi yaitu x = 2, atau x = 3. sehingga, penyelesaiannya yakni x = 2 atau x = 3.

Berdasarkan penjelasan di atas maka dapat kita tarik kesimpulan bahwa:
“Suatu pertidaksamaan apabila kedua ruasnya dikalikan dengan bilangan negatif yang sama maka tanda pertidaksamaan berubah”
Contoh:

3. Soal cerita
Soal certa 1.
Jumlah dua bilangan tidak lebih dari 120. Apabila bilangan kedua merupakan 10 lebihnya dari bilangan pertama, maka tentukan batas nilai untuk bilangan pertama.
Jawab:
Dari soal di atas, dapat kita ketahui bahwa terdapat dua besaran yang tidak diketahui. Yakni bilangan pertama dan juga bilangan kedua.
Maka berikutnya kita akan jadikan kedua besaran tersebut sebagai suatu variabel.
Sebagai contoh:
Dari soal tersebut juga kita ketahui bahwasannya bilangan kedua “10 lebihnya dari bilangan pertama”, maka akan berlaku hubungan seperti berikut:
y = x + 10
Dalam soal juga diketahui bahwa jumlah kedua bilangan “tidak lebih” dari 120.
Kalimat “tidak lebih” adalah tanda indikasi pertidaksamaan kurang dari sama dangan (≤). Sehingga, bentuk pertidaksamaan yang sesuai dengan soal yaitu pertidaksamaan kurang dari sama dengan.
Kemudian kita susun pertidaksamaannya seperti:
Sehinga, batas nilai untuk bilangan pertama tidak lebih dari 55.
Soal cerita 2.
- Tentukan model matematikan dari persamaan panjang kawat yang dibutuhkan dalam x.
- Apabila panjang kawat yang diapakai semuanya tidak lebih dari 132 cm, maka tentukan ukuran dari nilai maksimum dari balok tersebut.
Jawab:
Supaya kita lebih mudah untuk memahami soal di atas, maka perhatikan ilustrasi balok di bawah ini:
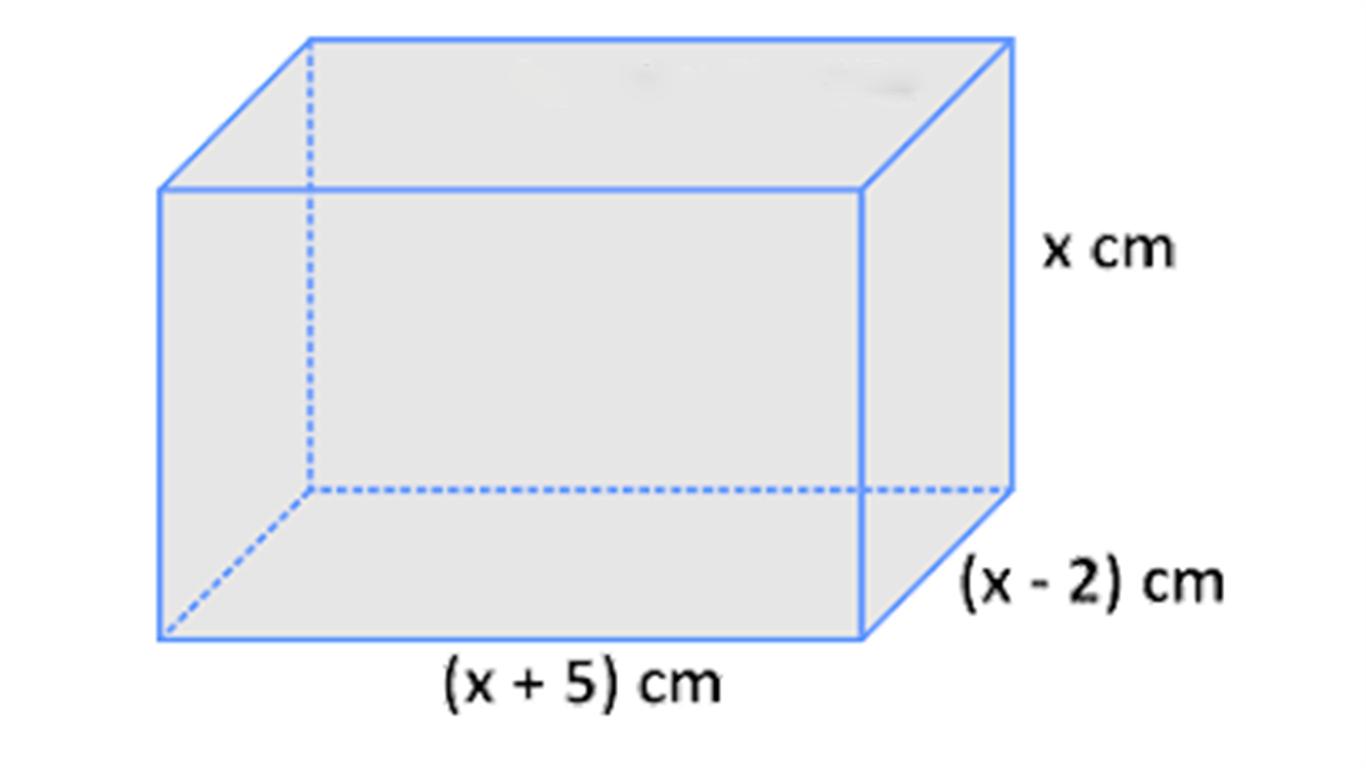
- Menentukan model matematika dari soal di atas.
Contohnya K menyatakan total dari panjang kawat yang diperlukan untuk membuat kerangka balok, maka total panjang kawat yang diperlukan merupakan jumlah dari keseluruhan rusuknya.
Maka, panjang K ialah sebagai berikut.
K = 4p (panjang) + 4l (lebar) + 4t (tinggi)
K = 4(x + 5) + 4(x – 2) + 4x
K = 4x + 20 + 4x – 8 + 4x
K = 12x + 12
Sehingga, kita dapatkan model matematika dari soal cerita nomor dua untuk panjang kawat total yakni K = 12x + 12.
- Menentukan ukuran maksimum balok dari soal di atas.
Panjang kawat tidak boleh melebihi panjang dari 132 cm maka model pertidaksamaannya bisa kita tulis sebagai berikut:
K ≤ 132
12x + 12 ≤ 132
Kemudian kita selesaikan pertidaksamaan linear satu variabel tersebut dengan menggunakan penyelesaian seperti berikuti ini:
12x + 12 ≤ 132
⇒ 12x ≤ 132 – 12
⇒ 12x ≤ 120
⇒ x ≤ 10
Dari penyelesaian x ≤ 10, maka nilai maksimum dari x yaitu 10. Dengan demikian, ukuran balok yakni untuk panjang, lebar dan juga tingginya ialah sebagai berikut:
Panjang = x + 5 ⇔ 10 + 5 = 15 cm
Lebar = x – 2 ⇔ 10 – 2 = 8 cm
Tinggi = x ⇔ 10 cm
Sehinaa kita dapatkan maksimum untuk balok tersebut adalah (15 × 8 × 10) cm.
Soal cerita 3.
Terdapat jumlah dari dua bilangan kurang dari 80. Bilangan kedua sama dengan tiga kali dari bilangan pertama.
Tentukan batas-batas dari kedua bilangan tersebut.
Jawab:
Andaikan bilangan pertama kita sebut sebagai x, maka bilangan kedua sama dengan 3x.
Jumlah kedua bilangan tersebut kurang dari 80. Oleh sebab itu, model matematikanya ialah seperti berikut ini:
x + 3x < 80 ⇔ 4x < 80
Penyelesaian model matematika ini yaitu 4x < 80 ⇔ x < 20.
Oleh sebab itu, batas bilangan pertama tidak lebih dari 20, sementara bilangan kedua tidak lebih dari 60.
Soal cerita 4.
Permukaan suatu meja yang berbentuk persegi panjang memiliki ukuran panjang 16x cm dan lebar 10x cm.
Apabila luasnya tidak kurang dari 40 dm2, maka tentukan ukuran minimum dari permukaan meja tersebut.
Jawab:
Diketahui panjang permukaan meja yaitu:
- (p) = 16x
- lebar (l) = 10 x
- luas = L.
Model matematika dari luas persegi panjang tersebut ialah sebagai berikut:
L = p × l
L = 16x × 10x
L = 160x2
Dari soal tersebut disebutkan bahwa luas tidak kurang dari 40 dm2 = 4.000 cm2 sehingga pertidaksamaannya bisa kita tulis seperti berikut ini:
L = 160x2 ≥ 4.000
160x2 ≥ 4.000
Kemudian kita selesaikan pertidaksamaan tersebut, dengan penyelesaian sebagai berikut:
160x2 ≥ 4.000
⇒ x2 ≥ 25
⇒ x ≥ ±5
Sebab ukuran besaran tidak boleh negatif, maka nilai minimum untuk x = 5 cm, sehingga kita dapatkan:
p = 16x cm = 16(5) cm = 80 cm
l = 10x cm = 10(5) cm = 50 cm
Sehingga, ukuran minimum dari permukaan meja tersebut yaitu (80 × 50) cm.
Soal cerita 5.
Suatu sepeda melaju di jalan raya dengan persamaan lintasan s(t) = t2 – 10t + 39.
Apabila x dalam meter dan t dalam detik, maka tentukan interval waktu supaya sepeda tersebut sudah menempuh jarak sekurang-kurangnya 15 meter.
Jawab:
Sepeda tersebut bisa menempuh jarak sekurang-kurangnya 15 meter, yang berarti s(t) ≥ 15.
Sehingga, model matematikanya yakni t2 – 10t + 39 ≥ 15. Model ini bisa kita selesaikan dengan cara seperti berikut ini:
t2 – 10t + 39 ≥ 15
⇒ t2 – 10t + 39 – 15 ≥ 0
⇒ t2 – 10t + 24 ≥ 0
⇒ (t – 6)(t – 4) ≥ 0
⇒ t ≤ 4 atau t ≥ 6
Dengan demikian, interval waktu supaya sepeda tersebut sudah menempuh jarak sekurang-kurangnya 15 meter yaitu t ≤ 4 detik atau t ≥ 6 detik.
Soal cerita 6.
Pak Irvan mempunyau sebuah mobil box pengangkut barang dengan daya angkut tidak lebih dari 500 kg.
Berat pak Irvan yaitu 60 kg serta dia akan mengangkut kotak barang yang setiap kotak beratnya 20 kg. Maka:
- Tentukan banyak kotak maksimum yang bisa diangkut oleh pak Irvan dalam sekali pengangkutan!
- Apabila pak Irvan akan mengangkut 115 kota, paling sedikit berapa kali kotak itu akan dapat terangkut semua?
Jawab:
Dari soal kita dapatkan beberapa model matematika seperti berikut:
- Contohnya x menyatakan banyak kota yang bisa diangkut oleh mobil untuk sekali jalan.
- Setiap kotak beratnya 20 kg, maka x kotak beratnya 20x kg.
- Total berat sekali jalan yaitu berat kotak ditambah dengan berat pak Irvan yakni 20x + 60.
- Daya angkut mobil tidak lebih dari, maka kita menggunakan tanda “≤”.
- Daya angkut tidak lebih dari 500 kg sehingga dari ketentuan (3) kita dapatkan model pertidaksamaan berikut=
20x + 60 ≤ 500
- Menentukan banyak kotak maksimum yang bisa diangkut dalam sekali jalan.
Menentukan banyak kotak berarti sama saja dengan menentukan nilai x, yakni dengan menyelesaikan pertidaksamaan di bawah ini:
20x + 60 ≤ 500
⇒ 20x ≤ 500 – 60
⇒ 20x ≤ 440
⇒ x ≤ 22
Dari penyelesaian tersebut, kita dapatkan nilai maksimum dari x yaitu 22. Dengan demikian, dalam setiap kali jalan mobil box dapat mengangkut paling banyak 22 kotak.
- Menentukan banyaknya keberangkatan untuk mengangkut 115 kotak
Supaya proses pengangkutan bisa dilakukan sedikit mungkin (minimum), maka setiap kali jalan harus mampu membawa kotak paling banyak 22 kotak.
Maka disini dapat kita dapatkan beberapa ketentuan sebagai berikut ini:
- Misalkan y menyatakan banyaknya keberangkatan (perjalanan).
- Setiap kali jalan mengangkut 22 kotak, maka untuk y perjalanan akan terangkut sebanyak 22y kotak.
- Akan diangkut 115 kotak, berarti untuk seluruh perjalanan minimal 115 kotak harus terangkut semua, sehingga kita dapatkan model matematika seperti berikut:
22y ≥ 115
Lalu, kita selesaikan pertidaksamaan linear di atas, dengan penyelesaian seperti berikut ini.
22y ≥ 115
⇒ y ≥115/22
⇒ y ≥ 5,227
Dari penyelesaian y ≥ 5,227 dan y bilangan bulat positif sebab menyatakan jumlah perjalanan, maka nilai minimum (terkecil) dari y yakni 6 (bilangan bulat).
Dengan demikian, dapat kita peroleh paling sedikit 6 kali perjalanan untuk mengangkut 115 kotak.
Pertidaksamaan Linear Dua Variabel (SPtLDV)
Pertidaksamaan Linear Dua Variabel (SPLDV)- merupakan suatu kalimat terbuka matematika yang di dalamnya memuat dua variabel. Dengan masing-masing variabel berderajat satu serta dihubungkan dengan tanda ketidaksamaan. Tanda ketidaksamaan yang dimaksud disini antara lain: >, <, ≤, atau ≥.
Maka, bentuk dari pertidaksamaan linear bisa kita tuliskan seperti berikut ini:
- ax + by > c
- ax + by < c
- ax + by ≥ c
- ax + by ≤ c
Berikut ini adalah contoh dari kalimat matematikanya:
2x + 3y > 6
4x – y < 9
Beberapa kalimat terbuka di atas menggunakan tanda hubung seperti <, >, > atau <. Yang menandakan kalimat tersebut merupakan pertidaksamaan.
Pertidaksamaan Linear Dua Variabel (SPLDV)
Berbeda halnya dengan penyelesaian dari persamaan linear dua variabel yang berwujud himpunan pasangan titik-titik.
Atau apabila kita gambar grafiknya akan berupa garis lurus.
Penyelesaian dari pertidaksamaan linear dua variabel berupa daerah penyelesaian.
Dalam praktiknya penyelesaian pertidaksamaan linear bisa berwujud daerah diarsir atau sebaliknya daerah penyelesaian pertidaksamaan linear dua variabel yang berupa daerah bersih.
Untuk menentukkan daerah penyelesaiannya, kita bisa melakukan langkah-langkah seperti di bawah ini:
- Ubahlah tanda ketidaksamaan dari pertidaksamaan menjadi tanda sama dengan (=), sehingga kita akan memperoleh persamaan linear dua variabel
- Gambar dari grafikatau garis dari persamaan linear dua variabel tadi.
Hal ini bisa kita lakukan dengan cara menentukan titik potong sumbu x dan sumbu y dari persamaan.
Ataupun dapat memakai dua titik sembarang yang dilewati oleh garis. Garis akan membagi dua bidang kartesius - Lakukan uji titik yang tidak dilewati oleh garis (substitusi nilai x dan y titik ke pertidaksamaan). Apabila menghasilkan pernyataan yang benar, artinya daerah tersebut adalah penyelesaiannya.
Tetapi, jika menghasilkan pernyataan salah maka bagian lainnya lah yang merupakan penyelesaiaanya.
Untuk lebih jelasnya perhatikan ulasan berikut ini.
Sistem Pertidaksamaan Linear Dua Variabel
Pertidaksamaan linear merupakan pertidaksamaan yang mana peubah bebasnya berbentuk linear (pangkat satu). Kalian tentunya masih ingatkan beberapa kalimat matematika di bawah ini.
- 2x ≥ 4; pertidaksamaan linear satu peubah
- 3x + y < 0; pertidaksamaan linear dua peubah
- x – 2y ≤ 3; pertidaksamaan linear dua peubah
- x + y – 2z > 0; pertidaksamaan linear tiga peubah
Dan kali ini, kami akan membahas seputar pertidaksamaan linear dengan dua peubah.
Gabungan dari dua atau lebih pertidaksamaan linear dua peubah disebut sebagai sistem pertidaksamaan linear dua peubah.
Berikut adalah contoh dari sistem pertidaksamaan linear dua peubah:
3x + 8y ≥ 24,
x + y ≥ 4,
x ≥ 0,
y ≥ 0.
1. Daerah Himpunan Penyelesaian Pertidaksamaan Linear Dua Peubah
Penyelesaian suatu pertidaksamaan linear dua peubah merupakan pasangan berurut (x,y) yang dapat memenuhi pertidaksamaan linear tersebut.
Himpunan dari penyelesaian tersebut dapat dinyatakan dengan sebuah daerah pada bidang kartesius (bidang XOY) yang diarsir.
Untuk lebih memahami daerah himpunan dari penyelesaian pertidaksamaan linear dua peubah. Berikut akan kami berikan contohnya:
Contoh:
Tentukan himpunan penyelesaian dari pertidaksamaan linear di bawah ini:
a. 2x + 3y ≥ 12 c. 4x – 3y < 12
b. 2x – 5y > 20 d. 5x + 3y ≤ 15
Jawab:
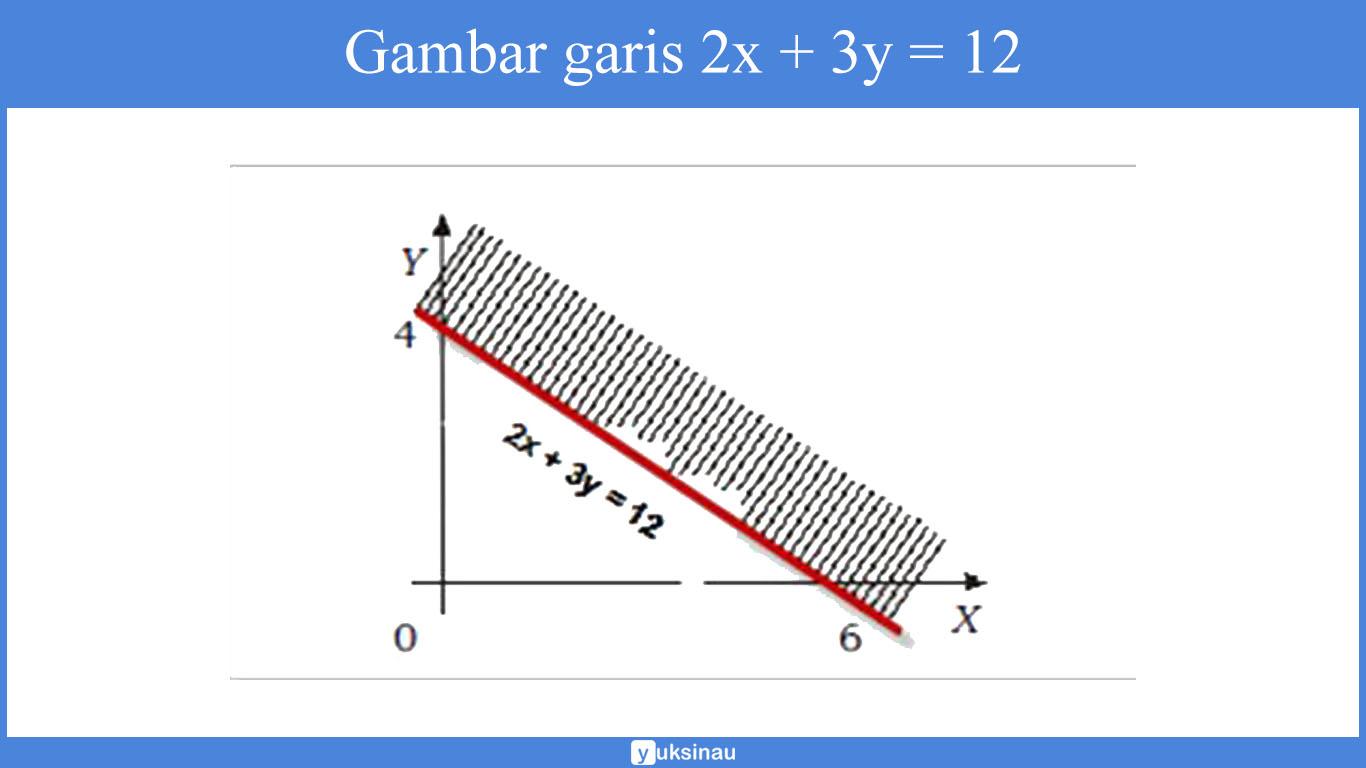
a. Langkah pertama adala lukis garis 2x + 3y = 12 dengan cara menghubungkan titik potong garis dengan sumbu X dan sumbu Y.
Titik potong garis dengan sumbu X memilki arti sebagai y = 0, dan didapatkan x = 6 (titik (6,0)).
Titik potong garis dengan sumbu Y artinya x = 0, didapat y = 4 (titik (0,4)).
Garis 2x + 3y = 12 tersebut kemudian akan membagi bidang kartesius menjadi dua bagian.
Untuk menentukan daerah yang mana adalah himpunan penyelesaian, maka dilakukan dengan mengambil salah satu titik uji dari salah satu sisi daerah.
Sebagai contoh disini kita ambil titik (0,0). Lalu disubstitusikan ke pertidaksamaan sehingga akan kita peroleh:
2 x0 + 3x 0 < 12
0 < 12
Sehingga, 0 ≥ 12 salah, yang berarti tidak dipenuhi sebagai daerah penyelesaian.
Jadi, daerah penyelesaiannya yaitu daerah yang tidak masuk dalam titik (0,0). Yakni daerah yang diarsir pada gambar di bawah ini:
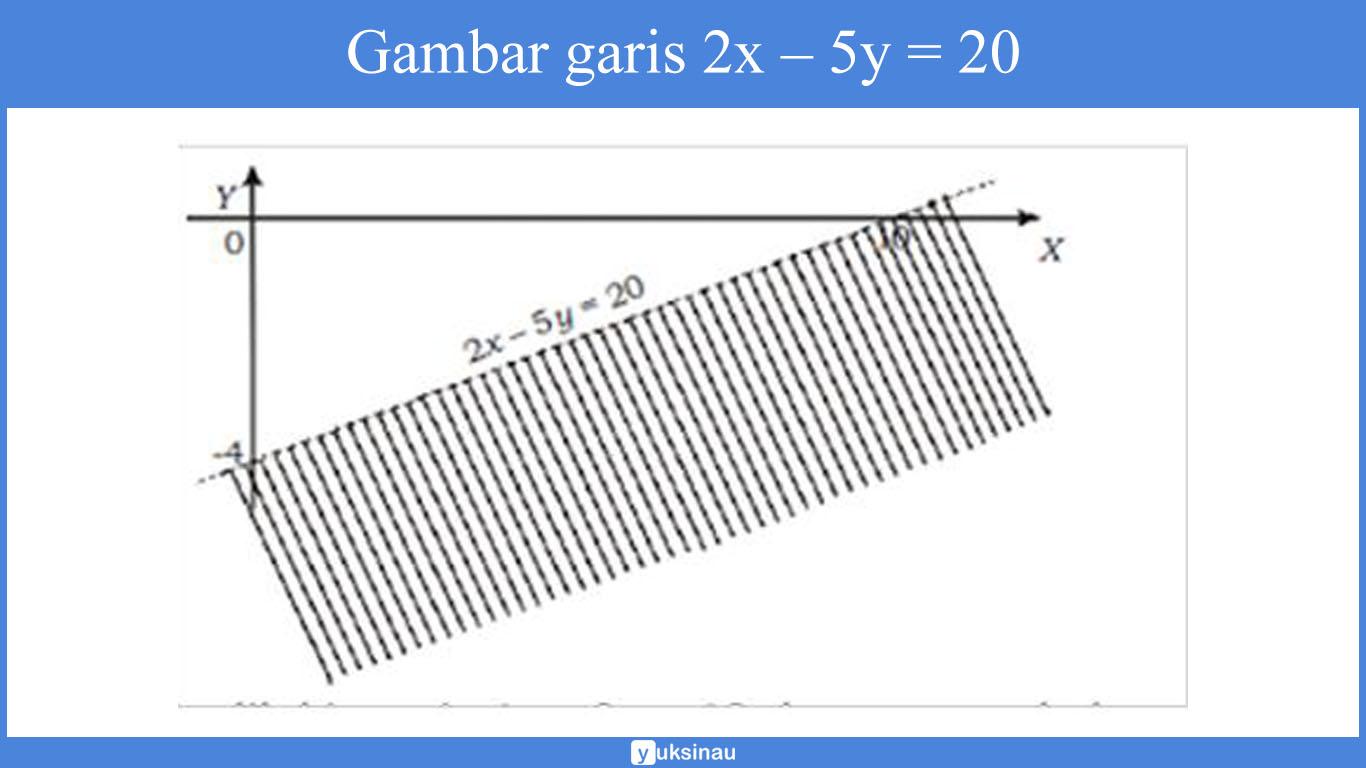
b. Langkah pertama adalah menggambar garis 2x – 5y = 20 dengan cara menghubungkan titik potong garis di sumbu X dan sumbu Y.
- Titik potong garis dengan sumbu X, y = 0, didapat x = 10 (titik (10,0))
- Titik potong garis dengan sumbu Y, x = 0, didapat y = –4 (titik (0,–4))
Garis 2x – 5y = 20 tersebut akan membagi bidang kartesius menjadi dua bagian.
Untuk menentukan daerah yang mana adalah himpunan penyelesaian. Maka kita akan melakukannya dengan cara mengambil titik uji pada salah satu sisi daerah.
Sebagai contoh kita ambil titik (0,0). Lalu kita substitusikan ke pertidaksamaan sehingga akan kita peroleh:
2 x0 – 5 x0 > 20
0 > 20 (salah), artinya tidak dipenuhi.
Sehingga, daerah penyelesaiannya yaitu daerah yang tidak masuk dalam titik (0,0). Yakni daerah yang diarsir pada gambar di bawah ini:
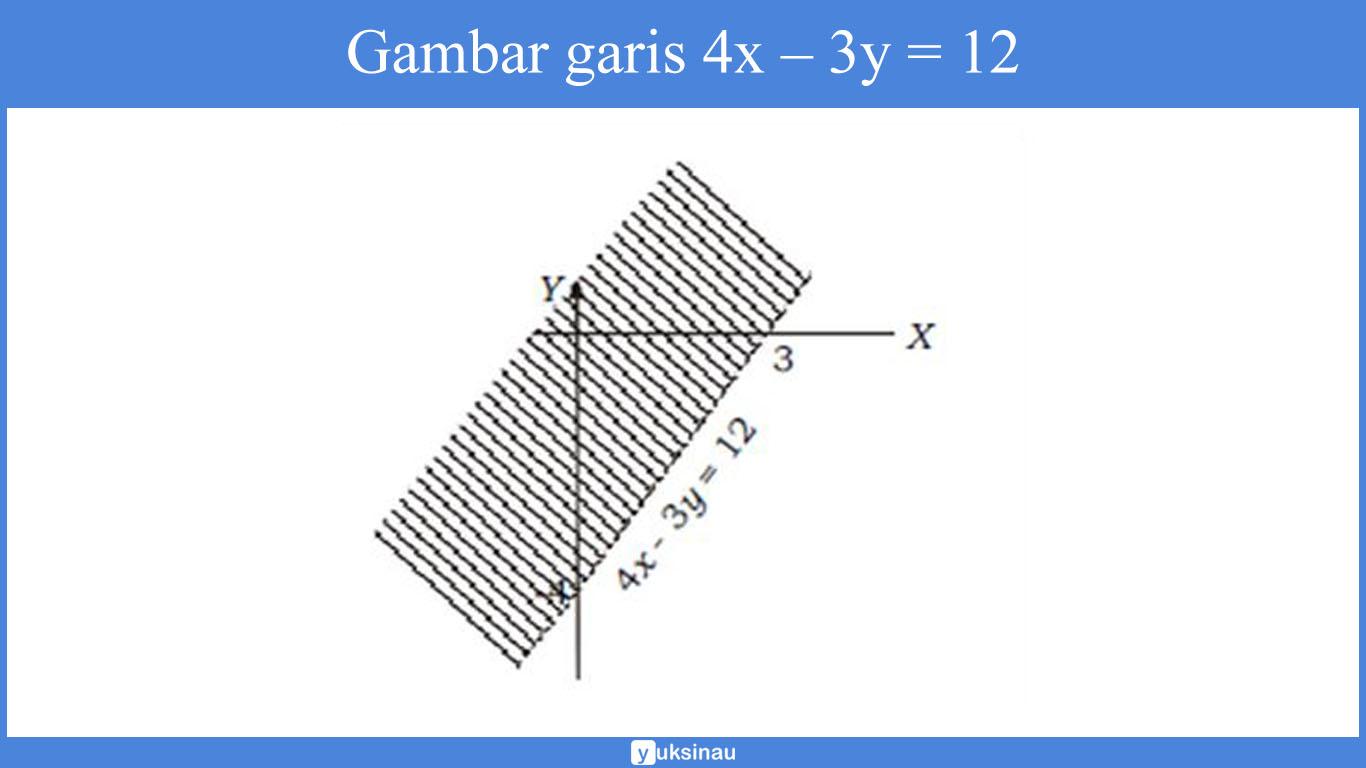
c. Langkah pertama adalah menggambar garis 4x – 3y = 12 dengan cara menghubungkan titik potong garis pada sumbu X dan sumbu Y.
- Titik potong garis dengan sumbu X maka y = 0 didapat x = 3 (titik (3,0))
- Titik potong garis dengan sumbu Y maka x = 0 didapat y = –4 (titik (0,–4))
Garis 4x – 3y = 12 tersebut akan membagi bidang kartesius menjadi dua bagian.
Untuk menentukan daerah yang mana adalah himpunan penyelesaian. Maka kita akan melakukannya dengan cara mengambil salah satu titik uji dari salah satu sisi daerah.
Sebagai contoh kita ambil titik (0,0). Lalu kita substitusikan ke pertidaksamaan sehingga akan kita peroleh:
4 x0 – 3x 0 < 12
0 < 12 (benar), yang berarti dipenuhi sebagai daerah penyelesaian.
Sehingga, daerah penyelesaiannya yaitu daerah yang terdapat atau memuat titik (0,0). Yakni daerah yang diarsir pada gambar di bawah ini:
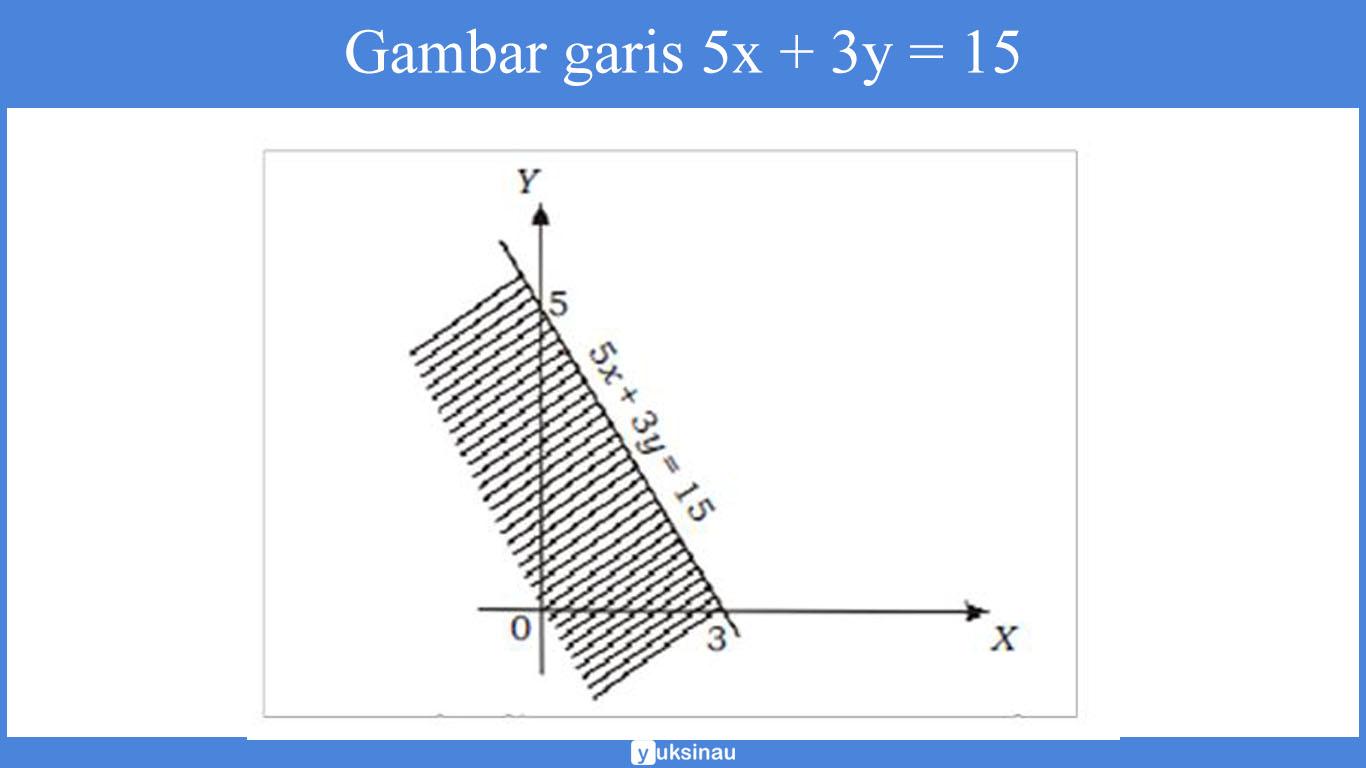
d. Langkah pertama adalah menggambar garis 5x + 3y = 15 dengan cara menghubungkan titik potong garis pada sumbu X dan sumbu Y.
- Titik potong garis dengan sumbu X maka y = 0, didapat x = 3 (titik (3,0))
- Titik potong garis dengan sumbu Y maka x = 0, didapat y = 5 (titik (0,5))
Garis 5x + 3y = 15 tersebut membagi bidang kartesius menjadi dua bagian.
Untuk menentukan daerah yang mana adalah himpunan penyelesaian. Maka kita akan melakukannya dengan cara mengambil salah satu titik uji dari salah satu sisi daerah.
Sebagai contoh kita ambil titik (0,0). Lalu kita substitusikan ke pertidaksamaan sehingga akan kita peroleh:
5 x0 + 3x 0 ≤15
0 ≤ 15 (benar), artinya dipenuhi.
Sehingga, daerah penyelesaiannya yaitu daerah yang terdapat atau memuat titik (0,0). Yakni daerah yang diarsir pada gambar di bawah ini:
Berdasarkan dari contoh di atas, cara untuk menentukan himpunan penyelesaian pertidaksamaan linear dengan dua peubah bisa kila laukan dengan beberapa langkah seperti di bawah ini:
1. Menggambar garis ax + by = c dalam bidang kartesius dengan cara menghubungkan titik potong garis pada sumbu X di titik (c/a ,0) serta pada sumbu Y di titik (0,c/b ).
2. Kita cari tahu sebuah titik uji yang berada di luar garis dengan cara menyubstitusikannya pada pertidaksamaan.
Apabila pertidaksamaan mampu terpenuhi (benar), maka daerah yang memuat titik tersebut adalah daerah himpunan penyelesaian.
Apabila pertidaksamaan tidak dipenuhi (salah), maka daerah yang tidak terdapat pada titik uji tersebut adalah daerah himpunan penyelesaian.
2. Daerah Penyelesaian Sistem Pertidaksamaan Linear
Himpunan penyelesaian sistem pertidaksamaan linear dua peubah merupaan himpunan titik-titik (pasangan berurut (x,y)) dalam bidang kartesius yang dapat memenuhi seluruh pertidaksamaan linear dalam sistem tersebut.
Sehingga daerah himpunan penyelesaiannya adalah irisan dari beberapa himpunan penyelesaian dari pertidaksamaan dalam sistem pertidaksamaan linear dua peubah itu.
Supaya kalian lebih mudah untuk memahami daerah penyelesaian dari sistem pertidaksamaan linear dua peubah, perhatikan beberapa contoh yang akan kami sajikan di bawah ini.
Contoh:
Tentukan daerah himpunan penyelesaian dari sistem pertidaksamaan di bawah ini:
a. 3x + 5y ≤ 15 b. x + y ≤ 6
x ≥ 0 2x + 3y ≤ 12
y ≥ 0 x ≥ 1
y ≥ 2
Jawab:
a. Langkah pertama adalah menggambar garis 3x + 5y =15, x = 0, dan y =0
Untuk 3x + 5y ≤ 15
Kemudian pilih titik (0,0), lalu kita substitusikan ke pertidaksamaan sehingga akan kita dapatkan:
3x 0 + 5x 0 ≤ 15
0 ≤ 15 (benar), yang berarti dipenuhi
Sehingga, daerah penyelesaiannya yaitu daerah yang memuat titik (0,0)
Untuk x ≥ 0, kita pilih titik (1,1) lalu disubstitusikan ke pertidaksamaan sehingga akan kita dapatkan:
1 ≥ 0 (benar), yang berarti dipenuhi.
Sehingga, daerah penyelesaiannya ialah daerah yang memuat titik (1,1)
Untuk y ≥ 0, kita pilih titik (1,1) lalu substitusikan ke dalam pertidaksamaan sehingga akan kita dapatkan:
1 ≥ 0 (benar), yang berarti dipenuhi.
Sehingga, himpunan penyelesaian dari soal tersebut adalah daerah yang memuat titik (1,1).
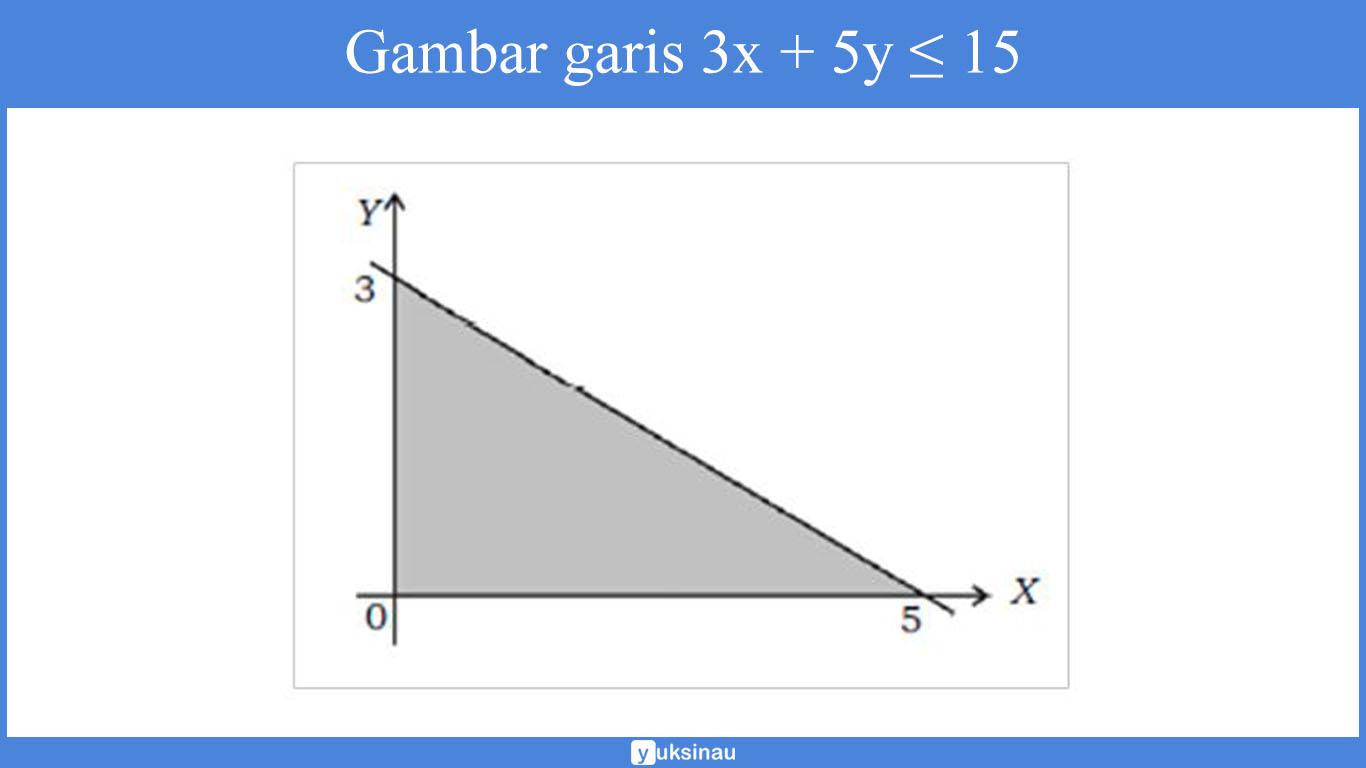
Daerah himpunan penyelesaian sistem pertidaksamaan adalah irisan dari ketiga daerah himpunan penyelesaian pertidaksamaan di atas.
Yakni yang tertera seperti pada gambar berikut ini (daerah yang diarsir).
b. Langkah pertama adalah menggambar garis x + y =6, 2x + 3y = 12, x = 1, dan y = 2.
Untuk x + y ≤ 6, kita pilih titik (0,0), lalu kita substitusikan ke pertidaksamaan sehingga akan kita dapatkan:
1 x0 + 1 x0 ≤ 6
0 ≤ 6 (benar), yang berarti dipenuhi.
Sehingga, daerah penyelesaiannya yaiu daerah yang memuat titik (0,0).
Untuk 2x + 3y ≤ 12, pilih titik (0,0), lalu kita substitusikan ke pertidaksamaan sehingga akan kita dapatkan:
2 x0 + 3x 0 ≤ 12
0 ≤ 12 (benar), yang berarti dipenuhi.
Sehingga dapat kita ketahui daerah penyelesaiannya yaitu daerah yang memuat titik (0,0).
Untuk x ≥ 1, pilih titik (2,1) lalu kita substitusikan ke pertidaksamaan sehingga kita dapatkan 2 ≥ 1 (benar) yang berarti dipenuhi.
Sehingga, daerah penyelesaiannya yaitu daerah yang memuat titik (2,1).
Untuk y ≥ 2, kita pilih titik (1,3) lalu disubstitusikan ke pertidaksamaan sehingga akan kita peroleh 3 ≥ 2 (benar) yang berarti dipenuhi.
Sehingga, himpunan penyelesaiannya berada di daerah yang memuat titik (1,3).
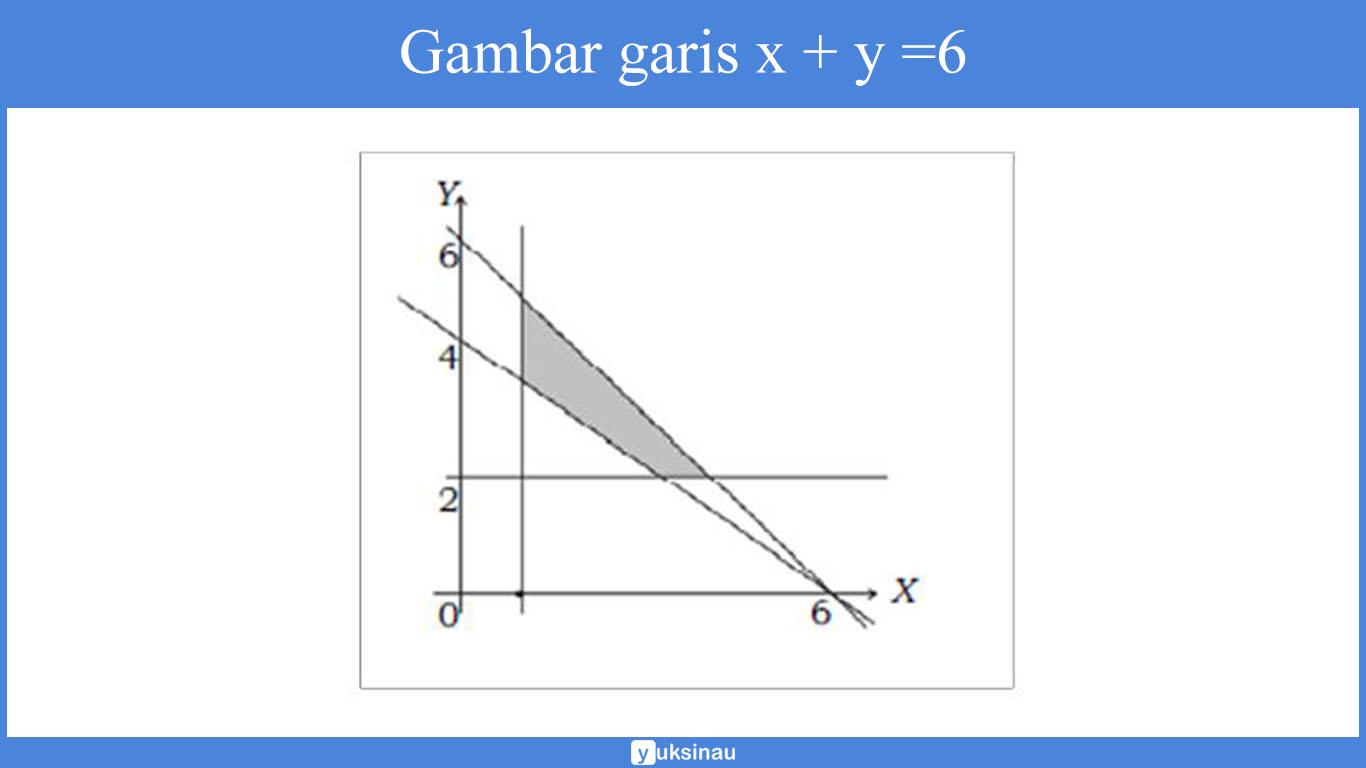
Daerah himpunan penyelesaian dari sistem pertidaksamaan tersebut adalah irisan dari ketiga daerah himpunan penyelesaian pertidaksamaan di atas.
Seperti yang terlihat pada gambar di samping (daerah yang diarsir).
b. Menentukan Sistem Pertidaksamaan jika Daerah Himpunan Penyelesaian Sistem Pertidaksamaan Linear Dua Peubah Diketahui
Cara menentukan daerah himpunan penyelesaian dari sistem pertidaksamaan linear dua peubah sudah kita pelajari di baba sebelumnya.
Sekarang bagaimana cara untuk menentukan sistem pertidaksamaan apabila daerah himpunan penyelesaiannya yang diketahui?
Simak penjelasannya berikut ini.
Contoh:
Daerah yang diarsir di bawah ini adalah daerah himpunan penyelesaiaan dari sebuah sistem pertidaksamaan linear dua peubah.
Maka, tentukanlah sistem pertidaksamaan tersebut.
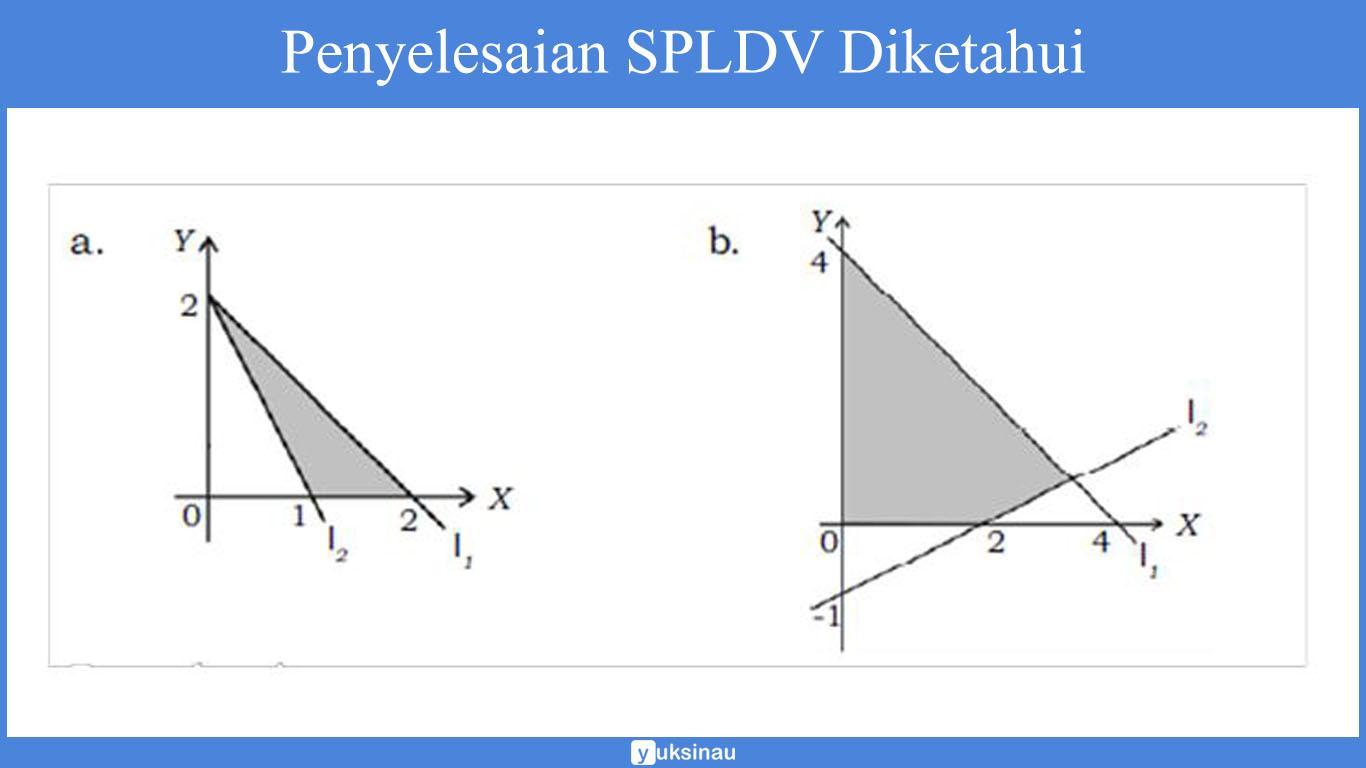
Jawab:
a. Garis l1 melalui titik (2,0) dan (0,2), persamaan garis l1 yaitu:
x/2 + y/2 = 1 menjadi x+y=2
Garis l2 melaui titik (1,0) dan (0,2), persamaan garis l2 yaitu:
x/1 + y/2 = 1 menjadi 2x+y=2
Dari gambar di atas, diketahui bahwa daerah himpunan penyelesaian (yang diarsir) terletak di bawah garis l1, di atas garis l2, di kanan sumbu Y, dan di atas sumbu X. Sistem pertidaksamaannya yakni:
x + y ≤ 2, 2x + y ≥ 2, x ≥ 0, dan y ≥ 0
b. Garis l1 melalui titik (4,0) dan (0,4), persamaan garis l1 yaitu:
x/4 + y/4 = 1 menjadi x+y=4
Garis l2 melalui titik (2,0) dan (0,–1), persamaan garis l2 yaitu:
x/2 + y/-1 = 1 menjadi -x+2y = -2
x-2y = 2
Dari gambar di atas, diketahui bahwa daerah himpunan penyelesaian (yang diarsir) terletak di bawah garis l1, di atas garis l2, di kanan sumbu Y, dan juga di atas sumbu X. Sistem pertidaksamaannya yakni:
x + y ≤ 4, x – 2y ≤ 2, x ≥ 0, dan y ≥ 0
Contoh Soal Cerita
Berikut akan kami berikan contoh dari soal cerita Sistem Persamaan Linear Dua Variabel (SPLDV) dalam kehidupan sehari-hari kehidupan sehari-hari yang diambil dari soal-soal Ujian Nasional.
Soal 1 (UN 2016)
Seorang tukang parkir mendapat uang sebesar Rp17.000,00 dari 3 buah mobil dan 5 buah motor, sedangkan dari 4 buah mobil dan 2 buah motor ia mendapat uang Rp18.000,00. Jika terdapat 20 mobil dan 30 motor, banyak uang parkir yang diperoleh adalah….
A. Rp135.000,00
B. Rp115.000,00
C. Rp110.000,00
D. Rp100.000,00
Jawab:
Misalkan:
Mobil = x dan motor = y
Ditanyakan: 20x + 30y = ….?
Model matematika:
3x + 5y = 17.000 ……(1)
4x + 2y = 18.000 ……(2)
Eliminasi persamaan (1) dan (2) akan didapatkan:
3x + 5y =17.000 | x4 |12x + 20y = 68.000
4x + 2y =18.000 | x3 |12x + 6y = 54.000 –
⟺ 14y = 14.000
⟺ y = 14.000/14
⟺ y = 1.000
Subtitusi nilai y = 1.000 ke salah satu persamaan:
3x+ 5y = 17.000
⟺ 3x + 5(1.000) = 17.000
⟺ 3x + 5.000 = 17.000
⟺ 3x = 17.000 – 5.000
⟺ 3x = 12.000
⟺ x = 12.000/3
⟺ x = 4.000
Maka, biaya parkir 1 mobil Rp4.000,00 dan 1 motor Rp1.000,00
20x + 30y = 20(4.000) + 30(1.000)
= 80.000 + 30.000
= 110.000
Sehingga, banyak uang parkir yang didapatkan sebesar Rp110.000,00
(Jawaban: C)
Soal 2 (UN 2015)
Di dalam kandang terdapat kambing dan ayam sebanyak 13 ekor. Jika jumlah kaki hewan tersebut 32 2kor, maka jumlah kambing dan ayam masing-masing adalah….
A. 3 dan 10
B. 4 dan 9
C. 5 dan 8
D. 10 dan 3
Jawab:
Misalkan:
Kambing = x dan ayam = y
Jumlah kaki kambing = 4 dan kaki ayam = 2
Ditanyakan: Jumlah kambing dan ayam = …?
Model matematika:
x + y = 13 ……(1)
4x + 2y = 32 ……(2)
Eliminasi persamaan (1) dan (2) akan kita dapatkan:
x + y = 13 | x4 | 4x + 4y = 52
4x + 2y = 32 | x1 | 4x + 2y = 32 –
⟺ 2y = 20
⟺ y = 20/2
⟺ y = 10
Subtitusi nilai y = 10 ke salah satu persamaan:
x + y = 13
⟺ x + 10 = 13
⟺ x = 13 – 10
⟺ x = 3
Sehingga, jumlah kambing = 3 ekor dan ayam = 10 ekor.
(Jawaban : A)
2. Pertidaksamaan Kuadrat
Pertidaksamaan kuadrat sama seperti yang ada pada pertidaksamaan linear yaitu bentuk “penghubung”antara ruas kanan dan kiri merupakan penggunaan tanda pertidaksamaan seperti kurang dari (<), kurang dari sama dengan (<), lebih dari (>) serta lebih dari sama dengan (>).
Namun terdapat perbedaan nih guys. Bentuk fungsi yang dioperasikan berwujud fungsi kuadrat dengan pangkat tertinggi yang dipunyai adalah pangkat dua.
ax2 + bc + c ** dx2 + ex + f
Keterangan:
- ** merupakan tanda pertidaksamaan seperti (<,> > atau <).
- a, b, c, d, e, f merupakan bilangan real dengan a,d ≠ 0.
Sekarang kita pelajari yuk mengenai bagaimana cara untuk penyelesaiannya. Seperti ini, terdapat beberapa poin penting untuk menyelesaikan pertidaksamaan kuadrat. Diantaranya ialah sebagai berikut:
a. Kumpulin terlebih dahulu seluruh suku ke dalam satu ruas, sebagai contonya ruas kiri. Nah, sehingga dengan cara tersebut tida terdapat suku atau pada ruas kanan kan, alias nol.
b. Berikutnya, selesaikan bentuk kuadrat dengan menggunakan metode pemfaktoran bentuk tersebut untuk mencari nilai yang memenuhi.
Kenapa? Hal ini dilakukan agar kalian lebih mudah bisa mengasumsikan tanda pertidaksamaan sebagai tanda sama dengan.
c. Bentuk himpunan penyelesaian kita dapatkan dengan cara menampilkan nilai pada garis bilangan. Nilai ini akan menjadi pembatas pada interval yang nantinya akan menjadi himpunan penyelesaian.
3. Pertidaksamaan Pangkat Tinggi
Berikutnya terdapat pertidaksamaan pangkat tinggi.
Pangkat tinggi disini bukan merupakan pangkat yang ada di dalam kemiliteran lho ya seperti mayor, kapten, letnan, dan jendral.
Melainkan, pertidaksamaan Pangkat Tinggi merupakan pertidaksamaan dengan derajat lebih dari dua.
Adapun bentuk dari “penghubung” antara ruas kanan dan kiri sama seperti yang ada pada pertidaksamaan linear dan pertidaksamaan kuadrat.
Diantaranya yaitu: kurang dari (<), kurang dari sama dengan (<), lebih dari (>) dan lebih dari sama dengan (>).
Berikut adalah bentuk umum dari pertidaksamaan pangkat tinggi:

Berikut ini adalah tahapan dalam penyelesaian pertidaksamaan pangkat tinggi, diantaranya yaitu:
a. Sama halnya yang ada pada pertidaksamaan kuadrat, kita harus memindahkan seluruh suku ke dalam satu ruas. Contohnya kita pindahkan pada ruas kiri sehingga tidak akan menyisakan suku atau bersisa nol pada ruas kanan.
b. Memfaktorkan bentuk tersebut ke dalam bentuk dengan derajat lebih rendah. Sebab bentuk dengan derajat yang lebih rendah akan membantu penyelesaian dalam hal mencari nilai.
c. Nilai yang telah diketahui, berikutnya disusun pada garis bilangan. Sama halnya dengan bentuk garis bilangan pada umumnya, kita harus mencari atau menentukan tanda pada tiap-tiap daerah.
4. Pertidaksamaan Pecahan
Pertidaksamaan pecahan ini berbentuk hampir sama dengan pecahan pada bilangan real.
Yang membedakan keduanya adalah di mana pembilang dan penyebutnya diisi oleh fungsi polinom. Bentuk umumnya juga masih sama dengan pertidaksamaan sebelumnya yang terdiri dari: kurang dari (<), kurang dari sama dengan (<), lebih dari (>) dan lebih dari sama dengan (>).
Berikut adalah bentuk umum dari pertidaksamaan pecahan, yaitu:

Berikut ini adalah tahapan dalam penyelesaian pertidaksamaan pecahan, diantaranya yaitu:
a. Pindahkan seluruh suku ke dalam satu ruas. Contohnya ruas kiri sehingga tidak akan menyisakan suku atau bersisa nol di ruas kanan.
Penting untuk kalian ingat nih guys, kita sangat dilarang untuk mengalikan silang penyebut dan juga pembilang antar ruas.
Kenapa hal itu dilarang? Karana nilai yang belum diketahui sangat memungkinkan untuk dapat mengubah bentuk pertidaksamaan jika kita melakukan kali silang.
b. Melakukan operasi aljabar dengan tujuan guna mendapatkan bentuk sederhana, baru setelah itu lakukan pemfaktoran supaya didapatkan nilai x.
c. Langkah terakhir yaitu menyusun nilai x tersebut ke dalam garis bilangan.
Seperti yang ada pada pertidaksamaan pangkat tinggi. Kita harus menentukan terlebih dahulu tanda pada masing-masing daerah secara manual.
Dengan cara mengambil satu nilai x di daerah tersebut lalu mengujinya pada bentuk peridaksamaan.
5. Pertidaksamaan Bentuk Akar
Pertidaksamaan bentuk akar yang akan kita pelajari untuk akar pangkat dua ya guys. Terdapat dua kemungkinan kasus dalam pertidaksamaan bentuk akar ini. Diantaranya yaitu:

Berikut ini adalah tahapan dalam penyelesaian pertidaksamaan bentuk akar, diantaranya yaitu:
Dalam contoh kasus A bisa kita lakukan dua cara, yaitu:
1. Menguadratkan kedua ruas.
2. Pengecekan syarat akar, di mana kita akan memastikan apabila fungsi di dalam akar pangkat dua haruslah bernilai positif atau sama dengan nol begitu juga dengan konstanta di ruas lainnya.
Berikutnya, pada contoh kasus B hampir sama dengan yang ada pada contoh kasus A yaitu dengan melakukan:
1. Menguadratkan kedua ruas.
2. Pengecekan syarat akar, di mana kita akan memastikan apabila fungsi di dalam akar pangkat dua haruslah bernilai positif atau sama dengan nol.
6. Pertidaksamaan Mutlak
Khusus untuk pertidaksamaan mutlak, maka kita harus mengingat aturan dari pertidaksamaan mutlak yang merupakan langkah penting dalam mengerjakan persoalan pertidaksamaan mutlak.
Berikut ini adalah tahapan dalam penyelesaian pertidaksamaan mutlak, diantaranya yaitu:
|f (x)| < a maka berlaku -a < f(x) < a
|f (x)| > maka berlaku f (x) < -a atau f(x) > a
|f (x)| = a maka berlaku f (x) = ±a, sehingga f (x) = a atau f (x) = -a dengan a ∈ R dan a > 0.
Demikianlah ulasan singkat terkait Pertidaksamaan yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.