Selain nilai sama yang menggunakan tanda “=”, ada juga bentuk pertidaksamaan baik itu lebih dari sebuah nilai atau kurang. Biasanya menggunakan tanda “>,<,≤,≥,≠”. Ada yang disebut pertidaksamaan irasional ada juga rasional.
Pelajaran tentang pertidaksamaan ini, sangat penting untuk dipahami sehingga saat menjawab soal-soal terkait akan lebih mudah.
Daftar Isi
Definisi Pertidaksamaan

Sebelum membahas secara detail tentang jenis dari pertidaksamaan, kamu harus tahu dulu apa arti dari istilah tersebut.
Dalam ilmu matematika dijabarkan sebagai sebuah pernyataan yang menjelaskan tentang adanya perbandingan antara dua atau lebih unsur atau objek.
Bisa juga disebut sebagai kalimat penjelasan dari dua pernyataan berbeda. Ada yang menggunakan simbol kurang maupun lebih, tapi bisa juga memakai simbol kurang dari atau lebih dari.
Baca: Perbandingan Matematika
Pertidaksamaan Rasional

Jenis pertidaksamaan ini menggunakan angka dalam bentuk pecahan. Bisa jadi pembilang maupun penyebutnya punya variabel masing-masing, bisa juga hanya bagian penyebutnya memiliki variabel.
Bentuk umum yang biasa dipakai untuk penjabarannya adalah:
> 0 atau ≥ ; g(x) ≠ 0
< 0 atau ≤ ; g(x) ≠ 0
Untuk menyatakan sebuah pertidaksamaan rasional, ada langkah yang perlu dilakukan. Dimulai dari menyatakannya dalam bentuk umum, kemudian menentukan pembuat nol yang ada pada pembilang dan penyebut.
Kemudian pembuat nol, akan ditulis pada sebuah garis bilangan dengan menentukan tanda yang tepat pada setiap interval.
Jika sudah, kamu tinggal menentukan mana daerah penyelesaiannya. Kalau dinyatakan besar dari atau besar sama dengan maka interval penyelesaian ada di bagian positif, sedangkan jika hasilnya kecil atau kecil sama dengan maka lokasi intervalnya yaitu bagian negatif dari daerah penyelesaian.
Ada dua hal yang tak boleh dilakukan, pada pertidaksamaan rasional pastinya akan berbeda dengan pertidaksamaan irasional yaitu:
- Mencoret faktor atau fungsi yang sama, baik pada pembilang maupun penyebut
- Melakukan perkalian silang
Apakah pertidaksamaan ini ada jenisnya? Ternyata ada empat dengan karakteristik masing-masing:
- Pertidaksamaan Rasional Linear Kuadrat
- Pertidaksamaan Rasional Kuadrat
- Pertidaksamaan Rasional Linear
- Pertidaksamaan Rasional Mutlak
Baca: Pertidaksamaan Linear Satu Variabel
Contoh Soal Pertidaksamaan Rasional

Biar lebih paham dan jelas, kamu perlu melihat langsung seperti apa contoh-contoh dari pernyataan yang bertolak belakang dengan pertidaksamaan irasional ini.
Contoh Soal 1
Berapa hasil dari pertidaksamaan :
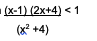
Jawabannya adalah:
Langkah 1= mengubah sisi kiri menjadi nol
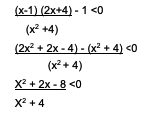
X2 + 4 merupakan definit yang positif, sehingga yang menjadi fokus adalah pembilang saja menjadi:
x2 + 2x – 8 <0
(x+4)(x-2) <0
Didapatkan titik kritis x ada pada -4 dan 2
Langkah 2= membuat garis bilangan dengan daerah penyelesaian menggunakan titik kritis
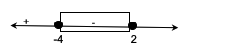
Langkah 3=menentukan himpunan penyelesaiannya yaitu {x|-4< x < 2}
Contoh Soal 2
3x +5x – 3 5
Berapa himpunan penyelesaiannya?
Langkah 1:
3x + 5x – 3 5
3x + 5x – 3 – 55 – 5
3x + 5x – 3 -50
Langkah 2:
Menyamakan penyebut dari pertidaksamaan:
3x+5-5(x-3)x-3 0
3x+5-5x+15X-3 0
-2x+20x-3 0
Langkah 3:
Memindahkan ruas dari pembilang dan penyebut
-2x + 20 = 0
20 = 2x
x = 10
x-3 = 0
x =3
Dengan diketahuinya nilai x, mana kamu perlu tahu lagi dimana posisi masing-masing nilai tersebut dengan acuan g(x) 0
Yang perlu diingat adalah, sehingga harus diganti dengan nol sehingga didapatkan himpunan penyelesaian menjadi x < 3 U x 10
Baca: Pertidaksamaan Linear Dua Variabel
Pertidaksamaan Irasional
Yang dimaksud dengan pertidaksamaan irasional, yaitu pertidaksamaan dengan fungsi pembentuk ada dalam tanda akar. Bisa di sisi kiri maupun kanan, dapat juga fungsi akar pada kedua sisi pertidaksamaan.
Makna lainnya adalah, ketika bilangan yang ada pada pertidaksamaan adalah bilangan asli maka nilai di bawah akar adalah < ; = 0
Cara utama untuk mencari hasil dari sebuah pertidaksamaan ini adalah, dengan mencari kuadrat dari setiap ruas yang ada. Lalu dikolaborasikan dengan rumus aljabar untuk interval yang sudah ditentukan.
Bentuk umum dari adalah:
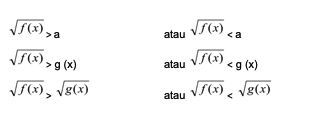
Untuk menyelesaikan pertidaksamaan ini, dibutuhkan beberapa pemahaman yang tepat, supaya hasilnya tidak salah.
- Pastikan untuk mengganti pertidaksamaan terlebih dahulu menjadi bentuk umum, dimana pada ruas kiri dibuat dalam bentuk perakaran
- Tentukan terlebih dahulu nilai pada ruas bagian kanan pertidaksamaan, dengan kondisi sebagai berikut:
a. Kalau nilainya nol atau positif
- Ruas kanan nol atau bilangan positif, maka ANda perlu membuat penyelesaian dari akibat dua ruas yang sudah dibuat kuadratnya
- Mencari penyelesaian pertidaksamaan irasional sesuai nilai yang dapat penuhi syarat bilangan bawah tanda akar
- Mencari irisan ketika penyelesaian sampai tuntas
b. Kalau nilainya negatif
- Tentukan penyelesaian pertidaksamaan ruas kanan < 0
- Tentukan penyelesaian nilai yang ada di bawah akar
- Mencari nilai yang mampu penuhi syarat untuk bilangan di bawah akah
c. Kalau nilainya lebih dari atau sama dengan nol
- Membuat uraian untuk ruas kanan menjadi < 0 atau ≥ 0
- Jika ruas kanan< 0, maka cari hasilnya terlebih dahulu, baru cari hasil untuk bagian selanjutnya
- Gabungkan hasil penyelesaian menjadi sebuah pertidaksamaan irasional yang utuh.
Contoh Soal Pertidaksamaan Irasional

Sama halnya dengan pertidaksamaan rasional, kamu juga perlu latihan menyelesaikan soal-soal yang berhubungan dengan pertidaksamaan irasional. Sehingga akan lebih paham tentang jenis pertidaksamaan ini.
Contoh Soal 1
Berapakah himpunan penyelesaian dari pertidaksamaan![]()
Jawab:
x + 3 ≥ 0
x≥ -3
Didapatkan himpunan penyelesaiannya adalah {x≥ -3}
Contoh Soal 2
Berapa himpunan penyelesaian dari 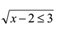
Jawab:
Syarat utamanya adalah x-2≥ 0
Kemudian diubah menjadi x≥2
Lalu lakukan kuadrat untuk kedua sisinya menjadi x – 2 ≤ 9 yang disederhanakan menjadi x ≤ 11.
Saatnya untuk membuat garis penyelesaian dengan mengacu pada hasil terakhir yang didapat.
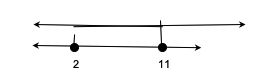
Jadi bisa disimpulkan bahwa himpunan penyelesaiannya adalah {x|2 ≤ x ≤ 11}
Kesimpulan
Dari penjelasan diatas tentang pertidaksamaan rasional dan pertidaksamaan irasional, diperoleh kesimpulan bahwa keduanya memiliki karakter yang berbeda.
Jenis rasional memiliki karakteristik, yaitu bilangan pecahan dengan pembilang dan penyebut yang harus dijabarkan dan pastinya hasil tidak boleh sama dengan nol.
Sedangkan irasional berhubungan dengan angka di bawah tanda akar, dimana pertidaksamaan juga tidak boleh sama dengan nol.
Untuk bisa menuntaskan berbagai soal, pemahaman tentang keduanya harus benar-benar maksimal supaya hasilnya tidak salah. Kamu juga harus paham persamaan garis, yang nantinya akan menjelaskan himpunan penyelesaian untuk masing-masing pertidaksamaan.
Sudah paham semua tentang pertidaksamaan irasional dan rasional? Semoga semua informasi di atas bisa kamu pahami dan dipakai sebagai referensi pengerjaan soal-soal seputar masalah pertidaksamaan.