Persamaan garis lurus menyatakan suatu persamaan yang mengartikan suatu garis lurus ke dalam suatu persamaan.
Ulasan materi yang akan dibahas melewati halaman ini merupakan gradien, rumus persamaan gairs lurus, dan juga metode atau cara untuk menentukan persamaan garis lurus.
Dalam bagian akhir akan kami berikan contoh cari soal materi ini sudah dilengkapi dengan pembahasan guna menambah pemahaman kalian mengenai persamaan garis lurus.
Karakteristik atau ciri dari persamaan garis lurus yaitu variabelnya mempunyai pangkat tertinggi satu.
Sebelum kalian mempelajari mater ini guna menentukan persamaan garis lurus, sebaiknya kalian terlebih dahulu membaca mengenai cara menggambar persamaan garis lurus.
Sebab, materi tersebut bisa membantu kalian untuk memahami materi persamaan garis lurus.
Garis lurus adalah suatu kumpulan titik-titik dengan jumlah tak terhingga serta saling berdampingan. Garis lurus bisa dinyatakan dalam berbagai bentuk persamaan garis lurus, satu garis lurus bisa dinyatakan dalam lebih dari satu persamaan.
Contoh untuk menyatakan persamaan garis lurus diantaranya yaitu:
- y = mx
- y = -mx
- y = a
- x = a
- ax + by = ab
- ax – by = -ab
- dan yang lainnya.
Di bawah ini adalah berbagai bentuk garis lurus sekaligus cara menyatakan persamaan garis lurus. Perhatikan baik-baik gambar di bawah ini:

Bentuk umum persa
maan garis lurus dinyatakan dalam persamaan y = mx + c, di mana m merupakan gradien, x adalah variabel, serta c merupakan konstanta.
Kita akan memulai ulasan materi persamaan garis lurus dengan pengertian dan juga definisi dari gradien. Berikut informasi selengkapnya.
Daftar Isi
Pengertian Persamaan Garis Lurus
Seperti yang telah kita sebutkan di atas, Persamaan garis lurus menyatakan suatu persamaan yang mengartikan suatu garis lurus ke dalam suatu persamaan. Sehingga,
Pengertian dari persamaan garis lurus merupakan suatu persamaan yang apabila kita gambarkan ke dalam suatu bidang koordinat Cartesius maka akan membentuk suatu garis lurus.
Dan yang di maksud dengan garis lurus yaitu kumpulan titik – titik yang letaknya sejajar.
Gradien
Tetapi, sebelum kita mempelajari lebih lanjut mengenai rumusnya. Kita terlebih dahulu harus mengetahi 1 komponen yang tidak dapat terlepas dari persamaan garis lurus. Yup, betuk sekali, yaitu Gradien.
Gradien merupakan suatu perbandingan komponen y dan juga komponen x , atau yang disebut juga dengan kecondongan sebuah garis. Simbol dari gradien yaitu berupa huruf m.
Gradien juga bisa didefinisikan sebagai suatu nilai yang menyatakan kemiringan suatu garis. Pada umumnya, nilai gradien dari sebuah persamaan garis lurus dinyatakan lewat perbandingan Δy/Δx.
Perhatikan cara untuk menentukan gradien pada gambar di bawah ini.
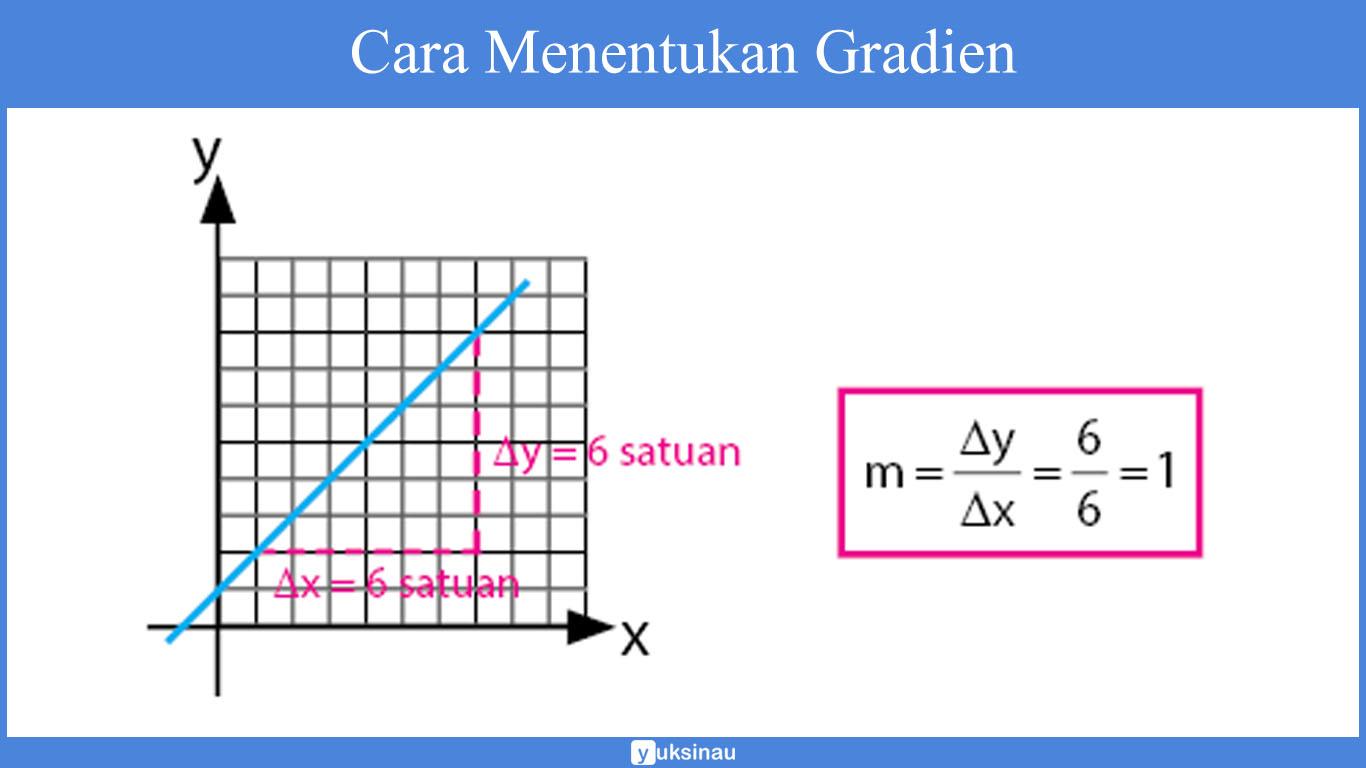
Cara untuk menentukan gradien pada sebuah garis lurus dalam bidang kartesius juga bisa dipengaruhi oleh arah kemiringan garis tersebut.
Simak lebih lanjut cara menentukan gradien garis pada pembahasan di bawah ini.
1. Gradien dari persamaan nya ax + by + c = 0
M = komponen X / komponen Y
2. Gradien yang melalui titik pusat nya ( 0, 0 ) dan titik ( a, b )
m = b / a
3. Gradien yang melalui titik nya ( x1, y1 ) dan ( x2, y2 )
m = y1 – y2 / x1 – x2 atau m = y2 – y1 / x2 – x1
4. Gradien garis nya saling sejajar ( / / )
m = sama atau apabila di simbolkan menjadi m1 = m2
5. Gradien garis nya saling tegak lurus ( lawan dan kebalikan )
m = -1 atau m1 x m2 = -1
Posisi Antara 2 Garis
Posisi antara 2 garis pada persamaan garis lurus bedakan menjadi 2 macam, antara lain sejajar dan tegak lurus.
Dua posisi tersebut mempunyai persamaan garis lurus yang saling berkaitan.
Sehingga, Apabila terdapat 1 persamaan garis lurus yang di ketahui, maka persamaan garis lurus yang saling sejajar atau tegak lurus dengan garis tersebut akan bisa kita ketahui.
Kemudian persamaan garis lurus tersebut memiliki syarat hubungan gradien. Syarat gradien dan juga gambar posisi antara 2 buah garis lurus akan di berikan pada ulasan yang ada di bawah ini. Simak baik-baik ya..
1. Garis Yang Saling Sejajar
Garis sejajar merupakan dua buah garis yang tidak pernah akan memiliki titik potong. Dua buah garis yang saling sejajar ini mempunyai gradien yang sama.
Diketahui gradien garis g = mg serta gradien garis h = mh. Sehingga, hubungan antara gradien 2 buah persamaan garis itu dapat di nyatakan dalam persamaan sebagai berikut:
mg = mh
2. Garis Yang Saling Tegak Lurus
Gradien dari dua buah garis yang saling tegak lurus juga mempunyai hubungan.
Hubungan dari dua buah garis tersebut di nyatakan jika gradien garis kedua adalah lawan dari kebalikan gradien garis yang pertama.
Atau dengan kata lain juga bisa dikatakan jika hasil dari perkalian 2 buah gradien tersebut sama dengan -1.
Sebagai contoh, gradien garis yang pertama mempunyai nilai m1 = 2 maka nilai dari gradien garis ke dua nya adalah m2 = -1/2.
Supaya kalian lebih memahami dengan lebih jelas, kalian dapat melihat pembahasan nya di bawah ini:
Diketahui gradien garis g = mg dan juga gradien garis h = mh . Sehingga, hubungan antara kedua gradien persamaan garis tersebut di nyatakan dalam persamaan sebagai berikut:
mg x mh = -1
Persamaan Garis Lurus
Suatu garis lurus bisa kita ketaui persamannya lewat rumus dan juga sedikit perhitungan.
Terdapat dua tipe soal persamaan garis lurus yang nantinya akan diberikan pada tingkat SMP.
Tipe yang pertama, soal yang diketahui gradien dan juga satu titik potong.
Sementara untuk tipe yang kedua yaitu persamaan yang diketahui dua titik potong.
Rumus untuk mencari persamaan garis itu akan kita bahas di bawah ini.
Terdapat dua rumus yang bisa kita pakai dalam menentukan persamaan garis lurus. Pemakaian rumusnya bergantung pada apa yang diketahui di soal.
Simak kedua rumus tersebut pada ulasan berikut ini:
1. Persamaan garis yang bergradien m dan melalui titik A(x1.y1)
y – y1 = m(x – x1)
2. Persamaan garis yang melalui titik A(x1.y1) dan B(x2.y2)
y – y1 / y2 . y1 = y – x1 / x2 . x1
Rumus Persamaan Garis Lurus
1. Persamaan Garis Lurus yang Bentuk Umum ( y = mx ).
Persamaan yang melalui titik pusat nya ( 0 , 0 ) serta bergradien m.
Sebagai contoh:
Tentukan persamaan dari garis lurus yang melalui titik pusat ( 0 , 0 ) dan juga bergradien 2
Jawab:
y = mx
y = 2 x
2. Persamaan Garis Lurus Melalui Titik Sejajar ( y = mx + c ).
Persamaan garis lurus yang / / dengan y = mx serta bergradien m.
Persamaan garis yang melalui titik nya ( 0 , c ) serta bergradien m. ( 0 , c ) adalah titik potong sumbu y.
3. Persamaan Garis Lurus Yang Melalui Titik Nya ( x1 , y1 ) Dan Bergradien m.
Persamaan nya yaitu sebagai berikut:
y – y1 = m ( x – x1 )
4. Persamaan Garis Lurus Yang Melalui 2 Titik Yaitu ( x1 , y1 ) Dan ( x2 , y2 ).
y – y1 / y2 – y1 = x – x1 / x2 – x1
Contoh Soal dan Pembahasan
Soal 1.
Tentukan persamaan dari garis lurus yang meleati titik potong garis – garis dengan persaamaan 3x + 2y – 12 dan 5x + 2y = 16 dan sejajar dengan garis 2x + y = 4 yaitu?
Jawab:
3x + 2y = 12
5x + 2y = 16
_________ –
– 2x = -4
x = -4 / -2 = 2
3x + 2y = 12
3 x 2 + 2y = 12
6 + 2y = 12
2y = 6
y = 6 / 2 = 3
Titik potong nya ( 2, 3 ) // 2x + y = 4
m1 = -a / b = -2 / 1 = -2
m1 = m2 = -2
y – y1 = m2 ( x – x1 )
y – 3 = -2 ( x – 2 )
y – 3 = -2x + 4
2x + y – 3 + 4 = 0
2x + y + 1 = 0
Soal 2.
Persamaan garis melalui (−1, 2) dan tegak lurus terhadap garis 4y = − 3x + 5 adalah ….
A. 4x – 3y + 10 = 0
B. 4x – 3y – 10 = 0
C. 3x + 4y – 5 = 0
D. 3x + 4y + 5 = 0
Jawab:
Mencari gradien garis 4y = –3x + 5:
4y= -3x + 5
y = -3/4x + 5/4
maka gradien garis tersebut yaitu m = – 3/4
Suatu garis akan tegak lurus dengan suatu persamaan garis apabila mempunyai gradien yang memenuhi:
m1 x m2 = -1
-3/4 x m2 = – 1
m2 = – 1 / -3/4
m2 = 4/3
Berikutnya, akan dicari persamaan garis dengan gradien m2 = 3/4 yang melewati titik (-1, 2)
y – y1 = m2 ( x – x1 )
y – 2 = 4/3 ( x – (-1))
y – 2 = 4/3 (x + 1)
3(y – 2) = 4 (x + 1)
3y – 6 = 4x + 4
– 4x + 3y – 10 = 0
4x – 3y + 10 = 0
Sehingga, jawaban yang tepat adalah A.
Soal 3. Soal UN Matematika Tahun 2013 dan 2008
Persamaan garis yang melalui titik (–3, 5) dan tegak lurus garis 3x – 2y = 4 adalah ….
A. 2x + 3y – 9 = 0
B. 2x – 3y – 9 = 0
C. 3x + 2y + 19 = 0
D. 3x – 2y – 1 = 0
Jawab:
Mencari gradien garis 3x – 2y = 4:
3x – 2y = 4
2y = 3x – 4
y = 3/2x – 2
Sehingga gradien garis tersebut yaitu m1 = 3/2
Suatu garis akan tegak lurus dengan suatu persamaan garis apabila mempunyai gradien yang memenuhi:
m1 x m2 = -1
3/2 x m2 = -1
m2 = -1/ 3/2
m2 = -2/3
Berikutnya, akan dicari persamaan garis dengan gradien m2 = -2/3 yang melewati titik (-3, 5)
y – y1 = m2 ( x – x1 )
y – 5 = -2/3 ( x – (-3))
y – 5 = -2/3 (x + 3)
3(y – 5) = -2 (x + 3)
3y – 15 = -2x – 6
2x + 3y – 15 + 6 = 0
2x + 3y – 9 = 0
Sehingga, jawaban yang tepat adalah A.
Soal 4. Soal UN Matematika Tahun 2009
Di antara persamaan garis berikut:
(I) 2y = 8x + 20
(II) 6y = 12x + 18
(III) 3y = 12x + 15
(IV) 3y = −6x + 15
yang grafiknya saling sejajar adalah ….
A. (I) dan (II)
B. (I) dan (III)
C. (III) dan (IV)
D. (II) dan (IV)
Jawab:
Sebuah grafik saling sejajar apabila mempunyai nilai gradien yang sama, yakni:
2y = 8x + 20 → m = 8/2 = 4
6y = 12x + 18 → m = 12/6 = 2
3y = 12x + 15→ m = 12/3 = 4
3y = 6x + 15→ m = -6/3 = -2
Sehingga, grafik yang saling sejajar terjadi pada persamaan garis (I) dan (III).
Sehingga, jawaban yang tepat adalah B.
Soal 5. Soal UN Matematika Tahun 2008
Persamaan garis lurus yang melalui titik A(–2, –3) serta tegak lurus terhadap garis dengan persamaan y = 2/3x + 9 adalah ….
A. 2x + 3y + 13 = 0
B. 3x + 2y + 12 = 0
C. 2x + 3y – 5 = 0
D. 3x – 2y = 0
Jawab:
Mencari gradien garis y = 2/3x + 9:
m1 = 2/3x
Suatu garis akan tegak lurus dengan suatu persamaan garis apabila mempunyai gradien yang memenuhi:
m1 x m2 = -1
2/3 x m2 = -1
m2 = -1/ 2/3
m2 = -3/2
Berikutnya, akan dicari persamaan garis dengan gradien m2 = -3/2 yang melewati titik (-2, -3)
y – y1 = m2 ( x – x1 )
y – (-3) = -3/2 ( x – (-2))
y + 3 = -3/2 (x + 2)
2(y + 3) = -3 (x + 2)
2y + 6 = -3x – 6
2y + 3x + 6 + 6 = 0
2y + 3x + 12 = 0
3x + 2y + 12 = 0
Sehingga, jawaban yang tepat adalah B.
Soal 6.
Persamaan garis yang sejajar dengan garis 2x+3y+6 = 0 dan melalui titik (-2,5) adalah …
a. 2x+3y-4 = 0
b. 2x-2y+16 = 0
c. 3y+2x-11 = 0
d. 3y-2x-19 = 0
Jawab:
Persamaan garis yang sejajar dengan 2x+3y+6 = 0 hal itu berarti gradien garisnya sama. Maka kita tentukan terlebih dahulu gradiennya dengan menggunakan cara seperti berikut ini:
2x+3y+6 = 0
⇔ 3y = -2x – 6
⇔ y = -2/3 x – 2
Sehingga dapat diketahui gradiennya = -2/3
Maka, persamaan garis tersebut secara umum yaitu y = -2/3x+c
Sebab garis tersebut melewati atau melalui titik (-2,5), maka titik tersebut dapat kita substitusikan pada persamaan untuk memperoleh nilai c. Berikut caranya:
y = -2/3x + c
⇔ 5 = -2/3 (-2) + c
⇔ 5 = 4/3 + c
⇔ c = 5 – 4/3
⇔ c = 15/3 -4/3
⇔ c = 11/3
Sehingga, persamaan garisnya yaitu:
y = -2/3x + c
⇔ y = -2/3 x + 11/3
⇔ 3y = -2x + 11
⇔ 3y + 2x – 11 = 0
Sehingga, jawaban yang tepat adalah C.
Soal 7.
Diketahui sebuah persamaan garis lurus yang melalui titik P(k,4) serta tegak lurus garis x+2y+1 = 0 yaitu y = m (x+1), sehingga nilai k adalah ….
a. 1
b. 2
c. 3
d. 4
Jawab:
x+2y+1 = 0
⇔ 2y = -x – 1
⇔ y = -1/2 x – 1/2
Sehingga dapat kita ketahui gradien (m) = -1/2
Sebab, kedua garis tersebut tegak lurus, maka
m.-1/2 =-m/2 = -1
⇔ -m = -2
⇔ m = 2
Atau cara mudahnya, apabila tegak lurus maka gradien garisnya lawan dan kebalikannya. Sebab, m dari garis x+2y+1 = 0 yaitu -1/2 maka lawan dan kebaliannya adalah 2.
Maka dari itu, persamaan garis y = m (x+1) akan menjadi y = 2(x+1)
garis y = 2(x+1) melewati titik (k,4) sehingga:
y = 2(x+1)
⇔ 4 = 2(k+1)
⇔ 4 = 2k + 2
⇔ 2k = 4-2
⇔ 2k = 2
⇔ k = 1
Sehingga, jawaban yang tepat adalah A.
Soal 8.
Diketahui suatu garis g : x-3y+5=0. Persamaan garis yang melewati titik (-2,11) dan juga tegak lurus persamaan garis g yakni …
a. -3x+5 c. 3x-5
b. -3x-5
c. 3x-5
d. 3x+5
Jawab:
x-3y+5=0
⇔ -3y = -x – 5
⇔ y = 1/3 x + 5/3
m1 = 1/3
Sebab tegak lurus maka dari itu:
1/3 . m2 = -1 ⇒ m2 = -3
Atau secara mudahnya m2 adalah lawan dan juga kebalikan dari m1.
persamaan garis yang bergradien -3 dan melewati titik (-2,11) yakni:
y-b = m (x-a)
⇔ y-11 = m2 (x-(-2))
⇔ y-11 = -3 (x+2)
⇔ y-11 = -3x -6
⇔ y = -3x – 6 +11
⇔ y = -3x +5
Sehingga, jawaban yang tepat adalah A.
Soal 9. (UN 2010)
Gradien garis dengan persamaan 3x-5y+15 adalah ….
a. 5/3
b. 3/5
c. -3/5
d. -5/3
Jawab:
Gradien garis dengan persamaan 3x-5y+15 =0 yakni:
3x-5y+15 = 0
⇔ – 5y = -3x – 15
⇔ 5y = 3x + 15
⇔ y = 3/5 x + 3
Gradien (m) = 3/5
Sehingga, jawaban yang tepat adalah B.
Soal 10.
Gradien dari persamaan 4y = 2x + 3 adalah …
A. m = 2
B. m = 1
C. m = ½
D. m = -½
Jawab:
Untuk persamaan garis yang berbentuk y = mx + c, maka gradien garisnya yaitu m (angka di belakang x).
Maka dari itu kita harus mengubah bentuk persamaan pada soal terlebih dahulu, dengan menggunakan cara sebagai berikut:
⇒ 4y = 2x + 3
⇒ y = (2/4)x + 3/4
⇒ y = ½x + 3/4
Dengan begitu, dapat kita ketahui gradiennya adalah:
⇒ y = ½x + 3/4
⇒ m = ½
Sehingga, jawaban yang tepat adalah C.
Soal 11.
Dari keempat persamaan garis berikut, yang memiliki gradien 2 yaitu….
A. y = 4x + 8
B. 4x + 2y – 5 = 0
C. 3y = 6x + 16
D. y + 2x = 6
Jawab:
Mari kita lihat graiden dari masing-masing opsi persamaan garis dari soal nomo 11 di atas:
A. y = 4x + 8 → m = 4
B. 4x + 2y – 5 = 0 → 2y = -4x + 5 → m = -4/2 = -2
C. 3y = 6x + 16 → y = 2x + 16/3 → m = 2
D. y + 2x = 6 → y = -2x + 6 → m = -2
Sehingga, persamaan garis yang mempunyai graiden 2 adalah 3y = 6x + 16.
Demikianlah ulasan singkat kali ini yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.
Satu pemikiran pada “Persamaan Garis Lurus”