Persamaan dan Pertidaksamaan Linier biasanya akan mulai kita pelajari saat kita berada di bangku kelas 10. Tepatnya bab 2 dari pelajaran matematika kelas 10.
Dan kali ini kita berkesempatan untuk membahas materi mengenai Persamaan dan Pertidaksamaan Linier. Informasi selengkapnya simak baik-baik ulasan di bawah ini ya.
Namun sebelum itu, untuk memudahkan pemahaman materi ini, akan kami berikan ilustrasi kegiatan sehari-hari yang berkaitan dengan materi Persamaan dan Pertidaksamaan Linier.
Daftar Isi
Ilustrasi Pembahasan
Berikut akan kami berikan cerita atau ilustrasi dari kegiatan sehari-hari. Perhatikan baik-baik ya..
Pada saat Gilang sedang tertidur lelap, tiba-tiba ibu membuka pintu dan membangunkan Gilang untuk membelikan martabak telur.
“Gilang, tolong beliin ibu martabak telur di warung sebelah untuk buka puasa nanti” kata ibu.
Kemudian, Gilang pun bangkit dari tempat tidurnya dan berkata “Ok bu, seinget Gilang harga buat martabak telur 8 ribu bu” kata Gilang.
“Ya udah” kata ibu sambil merogoh dompet. Kemudian ibu mengamil dua lembar uang dua puluh ribuan. “Nih uangnya, kamu beliin aja semuanya ya” kata ibu.
Dari cerita atau ilustrasi di atas nantinya akan kita cari tahu berapa banyak jumlah martabak telur yang harus dia beli.
Pada persoalan di atas, dapat kita selesaikan dengan menggunakan persamaan linear. Berikut ulasannya selengkapnya.
Persamaan linear
Persamaan linear merupakan suatu persamaan di mana pangkat variabelnya yaitu satu.
Adapun bentuk umum dari persamaan linear, seperti:
ax + b = c, a ≠ 0, a,b,c E R
Dari uraian cerita di atas, untuk meencari nilainya, maka kita perlu membuat “pembelian martabak telur” tadi menjadi sebuah persamaan linear.
Langkah pertama yang harus kita lakukan adalah menganggap jumlah martabak telur sama dengan “x”. Sebab dalam cerita di atas, Gilang harus menghabiskan uang 40 ribu untuk membeli “jumlah martabak telur yang belum diketahui”. Dengan harga satu bungkus martabak telur seharga 8 ribu, sehingga, kita buat kalimat matematikanya menjadi:
8000x = 40000
Jika sudah begini jadi gampang deh. Kemudian:
x = 40000/8000
x = 5 bungkus
Itu tadi merupakan salah satu contoh paling sederhana dari persamaan linear. Sudah tau kan apa itu persamaan linear?
Seperti yang telah disebutkan di atas, persamaan linear merupakan persamaan yang mengandung variabel berpangkat satu. Persamaan ini disebut juga sebagai persamaan berderajat satu atau persamaan linear satu variabel.
Dengan bentuk umumnya yaitu: ax + b = c, a ≠ 0, a, b, c, E R
Adapun sifat dari persamaan linear, antara lain:
Sifat Persamaan Linear
- Suatu persamaan tidak berubah nilainya apabila ditambah atau dikurang dengan bilangan yang sama.
- Suatu persamaan tidak berubah nilainya apabila kedua ruas dikalikan atau dibagi dengan bilangan yang sama.
Paham kan maksud dari sifat persamaan linear di atas?
Untuk memudahkan pemahaman kalian, coba kita pakai contoh dari persamaan martabak telur tadi ya.
8000x = 40000
Persamaan tersebut, tidak akan berubah jika kita ganti menjadi, sebagai contoh:
i) 8000x + 2000 = 40000 + 2000
ii) 8000x – 2000 = 40000 – 2000
Dalam persamaan linear, penjumlahan dan juga pengurangan angka di kedua ruas tidak akan mempengaruhi atau mengubah persamaan itu sendiri.
Yang berarti, persamaan martabak telur awal Gilang bernilai sama dengan persamaan i serta persamaan ii.
Hal tersebut juga berlaku jika nantinya kita ganti menjadi, sebagai contoh;
a) 8000x X 5 = 40000 X 5
b) 8000x : 5 = 40000 : 5
Persamaan awal dari martabak telur Rogu pun sejatinya sama dengan persamaan a dan juga b. Inilah yang dimaksud sebagai sifat-sifat persamaan linear.
Sama halnya dengan para pemuda lainnya, sebelum Gilang membeli martabak telur langganannya, Gilang kemudian berkeliling sebentar.
Atau istilah kerennya sih kita sebut dengan ngabuburit.
Di tengah perjalanannya, Gilang menjumpai sebuah papan rambu lalu lintas yang baru di dekat rumahnya. Bentuk dari papan rambu tersebut ialah seperti berikut ini:

Salah. Tanda itu bukan berarti penjual martabak telurnya pindah 30 km ke depan.
Namun, kecepatan berkendara di sana memiliki batas maksimal 30km/jam.
Gilang kemudian berpikir dalam hati, “Perasaan rambu ini kemaren nggak ada, deh.”
Ya, sebab belakang waktu ini memang banyak pengendara yang suka kebut-kebutan di daerah rumah Gilang.
Gilang juga sebenarnya sebal mengenai hal itu. Kebut-kebutan, motornya dimodifikasi, knalpotnya diganti jadi bersuara kencang. Beuh, suara kita, kan, jadi nggak kedengaran.
Niat untuk memesan“Bang, martabak telur 5 bungkus!” malah Abangnya mendengar Ging berkata, “Bebek belur bolu kukus!”
Di tengah pikirannya, Gilang teringat dengan pelajaran matematikanya di sekolah. Apabila ditulis dalam persamaan matematika dengan mengandaikan “kecepatan berkendara sebagai = x”, maka rambu tadi artinya: x < 30km/jam.
Tanpa sadar, hal tersebut termasuk ke dalam pertidaksamaan.
Pertidaksamaan Linear
Taukah kamu apa itu pertidak samaan linear? Pertidaksamaan merupakan suatu kalimat terbuka yang memakai tanda <, >, <, >.
Seperti persamaan linear, dalam pertidaksamaan linear juga memiliki beberapa sifat, diantaranya yaitu:
Sifat Pertidaksamaan Linear
- Suatu pertidaksamaan tidak akan berubah nilainya apabila ditambahkan atau dikurangkan dengan bilangan yang sama.
- Suatu pertidaksamaan tidak akan berubah nilainya apabila kedua ruasnya dikalikan atau dibagi dengan bilangan yang sama.
Jika kalian perhatikan baik-baik, sifat-sifat pertidaksamaan ini sama dengan yang ada pada sifat persamaan linear.
Lantas, apa yang menjadi perbedaan persamaan linear dengan pertidaksamaan linear?
Selain pada pemakaian “tanda, perbedaannya juga terdapat pada waktu saat pengali ataupun pembagian bilangan yang negatif”.
Dalam persamaan linear, jika kedua ruas kita kali atau bagi ke dalam bilangan negatif, maka “tanda”-nya akan tetap sama dengan (=).
Hal tersebut berbeda halnya dengan yang ada pada pertidaksamaan linear.
Dalam pertidaksamaan linear, jika terdapat kasus di mana kedua ruas dikali atau bagi dengan bilangan negatif (-), maka tanda yang sebelumnya akan berubah menjadi tanda sebaliknya.
Sebagai contoh:
-3x + 2 < 20
= -3x < 18
= 3x > -18 (perhatikan pada bagian ini. Tanda < berubah menjadi > pada waktu kedua ruas dikali dengan negatif (-))
= x > -6
Sifat Pertidaksamaan Linear
Atau sifat dari pertidaksamaan linear ini juga bisa pahami dengan beberapa uraian di bawah ini:
- Suatu pertidaksamaan tidak akan berubah tandanya apabila kedua ruas pertidaksamaan ditambah ataupun dikurangi dengan bilangan yang sama
Sebagai contoh: x > y maka x + a > y + a- Suatu pertidaksamaan tidak akan berubah tandanya apabila kedua ruas dikali atau dibagi dengan bilangan positif yang sama.
Sebagai contoh: x ≤ y maka a .x ≤ y. a dengan a > 0- Suatu pertidaksamaan akan berubah tandanya apabila kedua ruas dikali atau dibagi dengan bilangan negatif yang sama.
Sebagai contoh: x ≤ y maka –x a ≥ -y a (akan berubah tanda sebab kedua ruas dikali dengan bilangan negatif yang sama)
Sebagai contoh: x ≤ y maka x/-b ≥ y/ -b (berubah tanda karena kedua ruas dibagi dengan bilangan negatif yang sama.)
Contoh Soal dan Pembahasan
Berikut ini akan kami berikan beberapa contoh soal sekaligus pembahasannya mengenai Persamaan dan Pertidaksamaan Linier. Perhatikan baik-baik ya.
Soal 1. Pertidaksamaan Linear
Carilah himpunan penyelesaian dari pertidaksamaan di bawah ini:
b. 2 – 3x ≥ 2x + 12
b. 4x + 1 < x – 8
Jawab:
a. 2 – 3x ≥ 2x + 12
⇒ −2x – 3x ≥ −2 + 12
⇒ −5x ≥ 10
⇒ x ≤ −2
Sehingga, himpunan penyelesaian pertidaksamaan dari soal nomor 1 yaitu {x | x ≤ −2, x ∈ R}.
b. 4x + 1 < x – 8
⇒ 4x – x < −8 – 1
⇒ 3x < −9
⇒ x < −3
Sehingga, himpunan penyelesaian pertidaksamaan dari soal nomor 1 yaitu {x | x < −3, x ∈ R}.
Soal 2. Pertidaksamaan Linear
Tentukan himpunan penyelesaian dari:
a. 2x – 3 < 4x – 3 < 2x + 2
b. 2x < 3x + 10 < 4x
Jawab:
a. 2x – 3 < 4x – 3 < 2x + 2
⇒ −3 < 2x – 3 < 2 ..………………….(maasing-masing ruas dikurangi 2x)
⇒ 0 < 2x < 5 ………..………..……….(maasing-masing ruas ditambah 3)
⇒ 0 < x < 5/2 ………………………….(maasing-masing ruas dibagi 2)
Sehingga, himpunan penyelesaiannya yaitu {x | 0 < x < 5/2}.
b. 2x < 3x + 10 < 4x
⇒ 0 < x + 10 < 2x …………………(maasing-masing ruas dikurangi 2x)
Sekarang, perhatikan cara di bawah ini:
0 < x + 10 < 2x sama artinya dengan:
(1) x + 10 > 0
(2) 2x > x + 10
Pandang pertidaksamaan dari no (1), x + 10 > 0 ⇔ x > −10
Pandang pertidaksamaan dari no (2), 2x > x + 10 ⇔ x > 10
Penyelesaian dari pertidaksamaan (1) dan (2) bisa kita gambarkan seperti gambar di bawah ini:
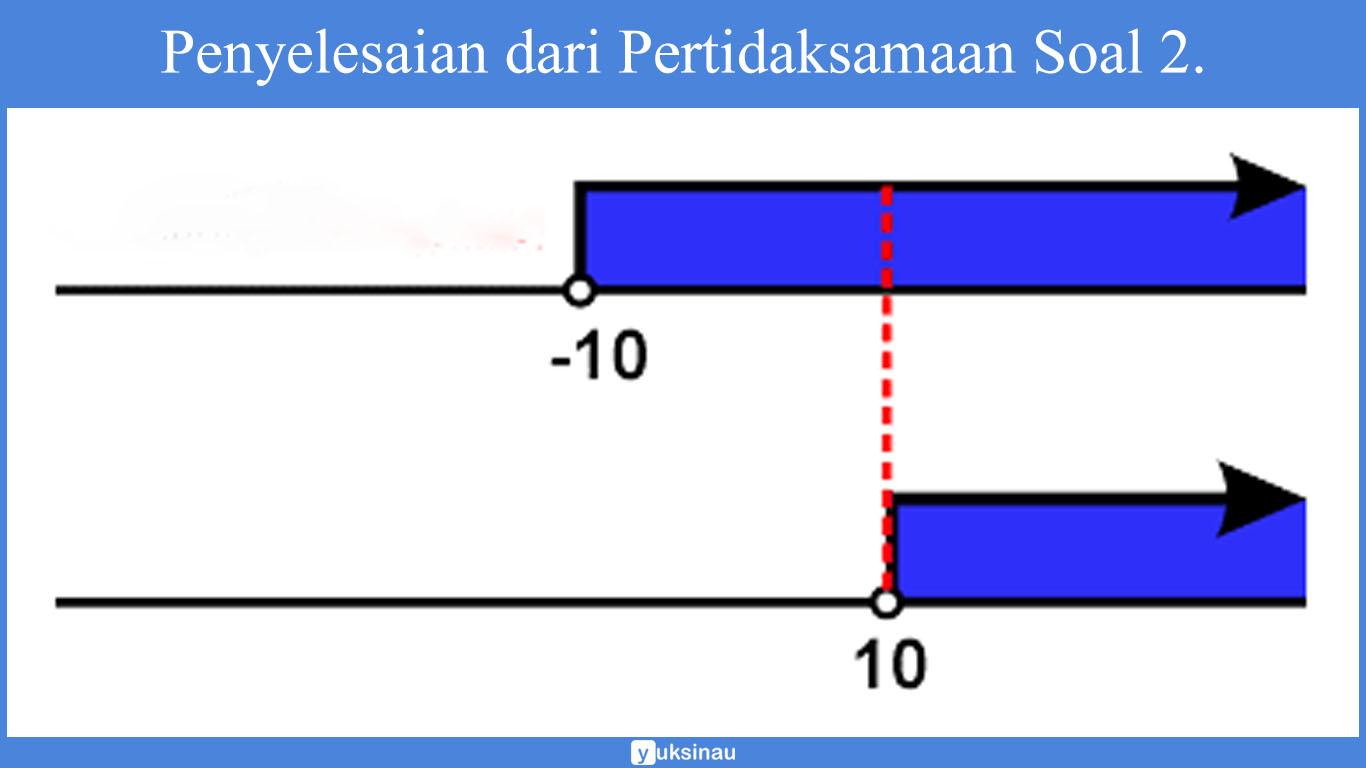
Sehingga, himpunan penyelesaiannya yaitu {x | x > 10}.
Sifat Pertidaksamaan Linear
- Apabila kedua ruas ditambah atau dikurangi dengan bilangan yang sama, maka tanda pertidaksamaan tetap.
- Apabila kedua ruas pertidaksamaan dikali atau dibagi dengan bilangan positif, maka tanda pertidaksamaan tetap.
- Apabila kedua ruas pertidaksamaan dikali atau dibagi dengan bilangan negatif, maka tanda pertidaksamaan dibalik.
Soal 3. (UN 2015) Persamaan Linear (SPLDV)
Di dalam kandang terdapat kambing dan ayam sebanyak 13 ekor. Jika jumlah kaki hewan tersebut 32 2kor, maka jumlah kambing dan ayam masing-masing adalah….
A. 3 dan 10
B. 4 dan 9
C. 5 dan 8
D. 10 dan 3
Jawab:
Misalkan:
Kambing = x dan ayam = y
Jumlah kaki kambing = 4 dan kaki ayam = 2
Ditanyakan: Jumlah kambing dan ayam = …?
Model matematika:
x + y = 13 ……(1)
4x + 2y = 32 ……(2)
Eliminasi persamaan (1) dan (2) akan kita dapatkan:
x + y = 13 | x4 | 4x + 4y = 52
4x + 2y = 32 | x1 | 4x + 2y = 32 –
⟺ 2y = 20
⟺ y = 20/2
⟺ y = 10
Subtitusi nilai y = 10 ke salah satu persamaan:
x + y = 13
⟺ x + 10 = 13
⟺ x = 13 – 10
⟺ x = 3
Sehingga, jumlah kambing = 3 ekor dan ayam = 10 ekor.
(Jawaban : A)
Baca juga:
- Pertidaksamaan Linear Satu Variabel (PtLSV)
- Pertidaksamaan Linear Dua Variabel (SPtLDV)
- Sistem Persamaan Linear Dua Variabel (SPLDV)
- Sistem Persamaan Linear Tiga Variabel (SPLTV)
Demikianlah ulasan singkat kali ini yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.
4 pemikiran pada “Persamaan dan Pertidaksamaan Linier”