Geometri Bidang Datar merupakan sebutan untuk berbagai bangun-bangun dua dimensi. Bangun datar adalah sebuah bidang datar yang dibatasi oleh garis lurus maupun garis lengkung. –sc: wikipedia
Geometri Bidang Datar juga membahas mengenai konsep jarak baik antara dua titik maupun jarak titik ke garis. Di samping itu juga membahas mengenai titik tengah antara dua titik.
Daftar Isi
Geometri Bidang Datar
A. Sudut
Sudut yang ada di dalam geometri merupakan suatu besaran rotasi pada sebuah ruas garis dari satu titik pangkalnya ke posisi yang lain.
Tak hanya itu saja, dalam bangun dua dimensi yang beraturan, sudut bisa juga didefinisikan sebagai sebagai ruang antara dua buah ruas garis lurus yang saling berpotongan.
Total besar dari sudut pada lingkaran adalah 360°. Total besar sudut pada segitiga siku-siku 180°. Besar sudut pada persegi atau segi empat adalah 360°. Untuk mengukur sudut bisa kita manfaatkan alat ata penggaris busur derajat.
Macam-macam Sudut
1. Sudut Lancip
Sudut lancip merupakan sudut yang besarnya lebih kecil dari 900 serta lebih besar dari 00 (00< a <900 )
2. Sudut Siku-siku
Sudut siku-siku merupakan sudut yang besarnya 900
3. Sudut Tumpul
Sudut tumpu; merupakan sudut yang besarnya lebih kecil dari 1800 serta lebih besar dari 900 (900 < a<1800 )
4. Sudut Lurus
Sudut lurus merupakan sudut yang besarnya 1800
5. Sudut Lingkaran Penuh
Sudut lingkaran penuh merupakan sudut yang besarnya 3600
Bangun Datar
Bagian-bagian Bangun Datar
1. Titik (.)
Titik adalah suatu noktah, sehingga tidak mempunyai panjang. Titik merupakan suatu bentuk yang paling sederhana dari geometri. Hal ini disebabkan titik hanya dipakai untuk menunjukkan posisi.
Titik A
2. Garis.
Suatu garis (garis lurus) bisa kita bayangkan sebagai kumpulan dari titik – titik yang memanjang secara tak terhingga pada ke kedua arah.
Jika 2 titik dihubungkan maka akan didapatkan suatu suatu garis.
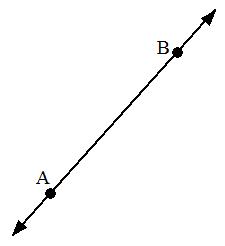
3. Bidang
Suatu bidang bisa kita anggap sebagai kumpulan titik yang jumlahnya tak terhingga sehingga akan membentuk permukaan rata yang melebar ke segala arah sampai tak terhingga.
Keliling dan Luas Bangun Datar
1. Bujur sangkar (Persegi sama sisi)
Suatu bangunan segi empat di mana keempat sisinya memiliki sama panjang serta keempat sudutnya adalah sudut siku-siku.
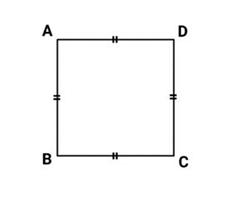
Panjang :
AB = BC = CD = DA
Sebab panjang sisi-sisinya sama maka keliling dalam suatu persegi dinyatakan dengan:
K = AB + BC + CD + DA’
Rumus yang biasa digunakan adalah:
K = 4s
L = s x s
L = s 2
Contoh soal:
Tentukanlah keliling dan juga luas dari sebuah persegi yang memiliki sisi 5 cm!
Jawab:
K = 4s
= 4.5
= 20 cm
L = s x s
= 5 x 5
= 25 cm2
2. Persegi panjang
Persegi panjang sesuai dengan namanya merupakan suatu bangunan segi empat yang kedua sisi yang berhadapan sama panjang serta keempat sudutnya adalah sudut siku-siku.
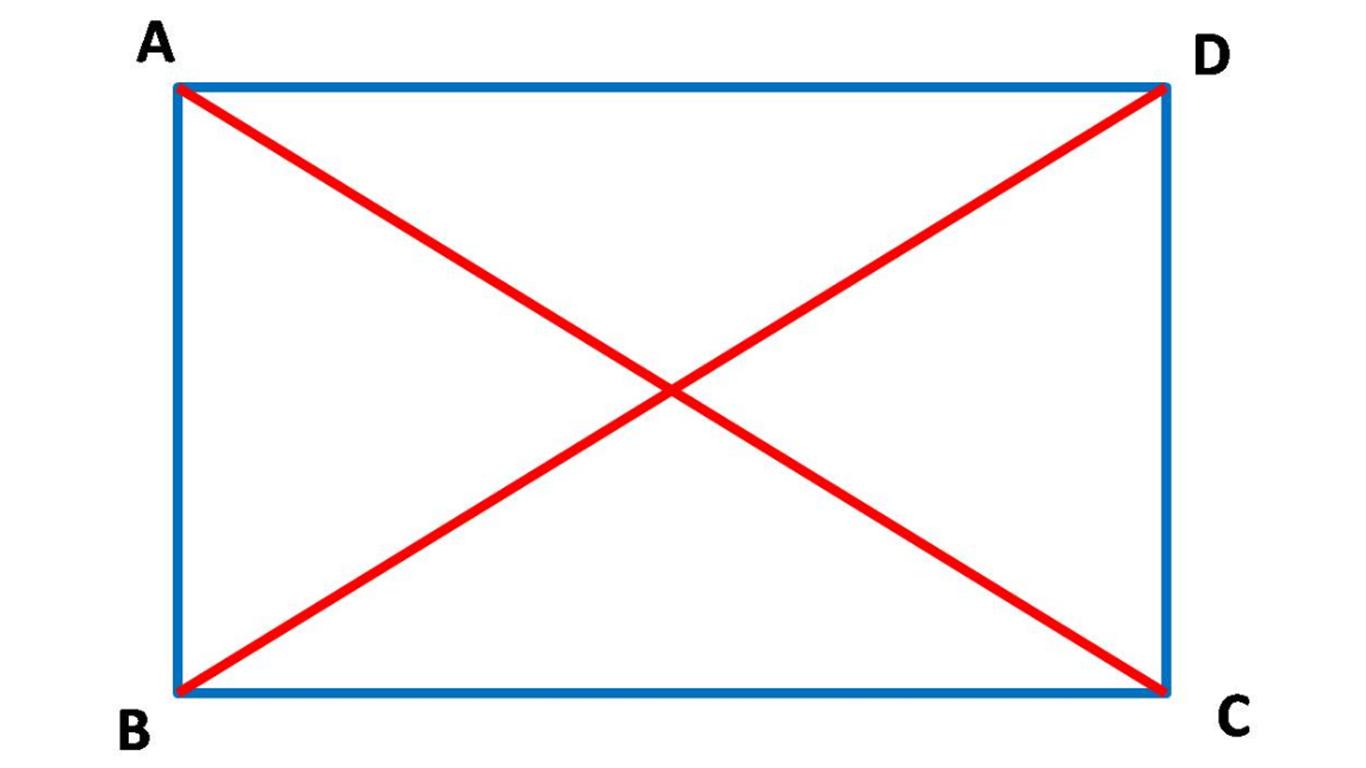
Panjang:
AB = CD (p)
BC = DA (l)
Rumus yang biasa digunakan adalah:
K = 2p +2l
K = 2(p + l)
L = p x l
Contoh soal:
Tentukan keliling dan juga luas dari suatu persegi panjang yang memiliki panjang 8 cm dan lebar 4 cm!
Jawab:
K = 2(p + l)
= 2(8 + 4)
= 2(12)
= 24 cm
L = p x l
= 8 x 4
= 32 cm2
3. Segitiga
Segitiga merupakan sebuah bangun datar yang jumlah sudutnya sebesar 1800 serta dibentuk dengan cara menghubungkan tiga buah titik yang tidak segaris dalam satu bidang.
Adapun beberapa jenis segitiga, diantaranya yaitu:
1. Segitiga Sama Sisi
Segitiga sama sisi yakni segitiga di mana ketiga sisinya memiliki panjang yang sama atau sama panjang.
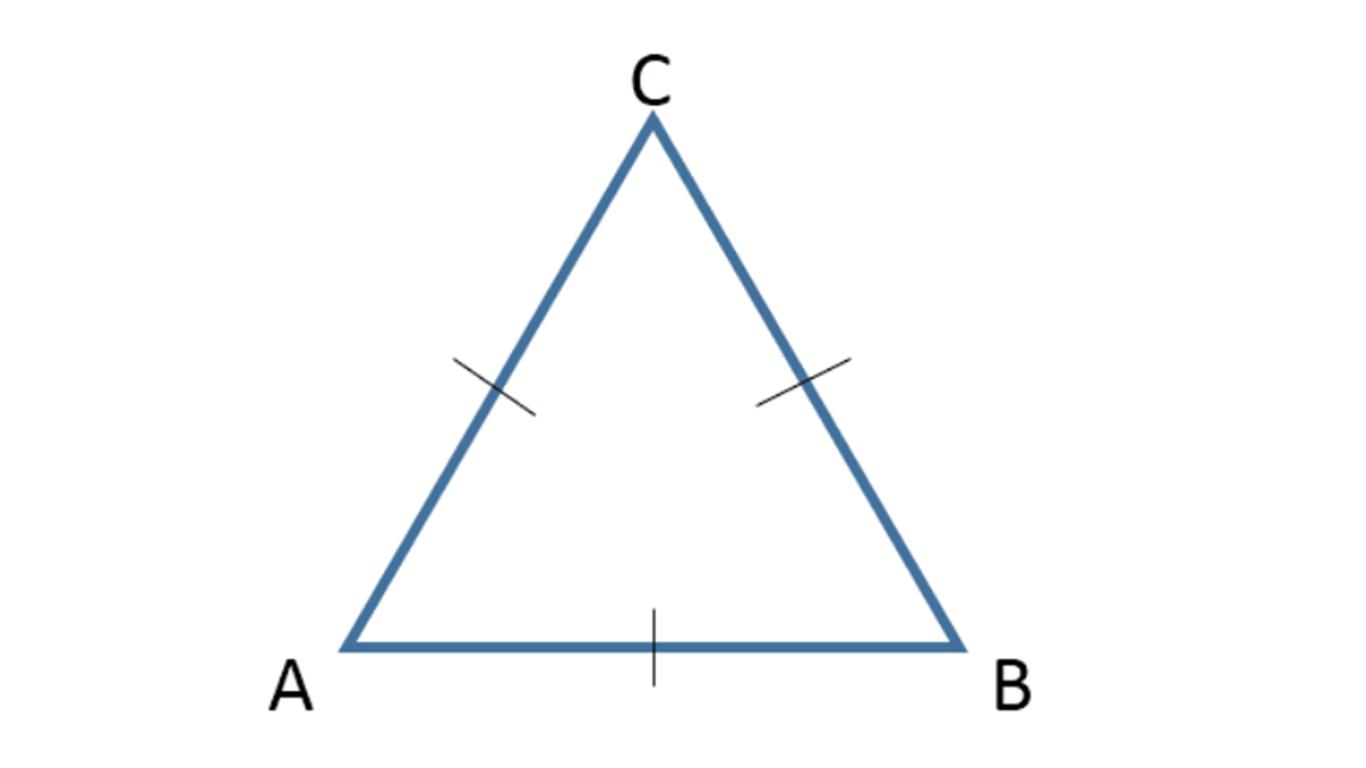
Panjang AB = BC =CA
∠A = ∠B = ∠C = 600
∠A + ∠B + ∠C = 1800
K = AB + BC + AC
Rumus yang biasa digunakan adalah:
K = 3s
Luas = 1/2. alas . tinggi
2. Segitiga Sama Kaki
Segitiga sama kaki merupakan segitiga yang memiliki dua sudut yang sama serta dua buah sisi yang sama.
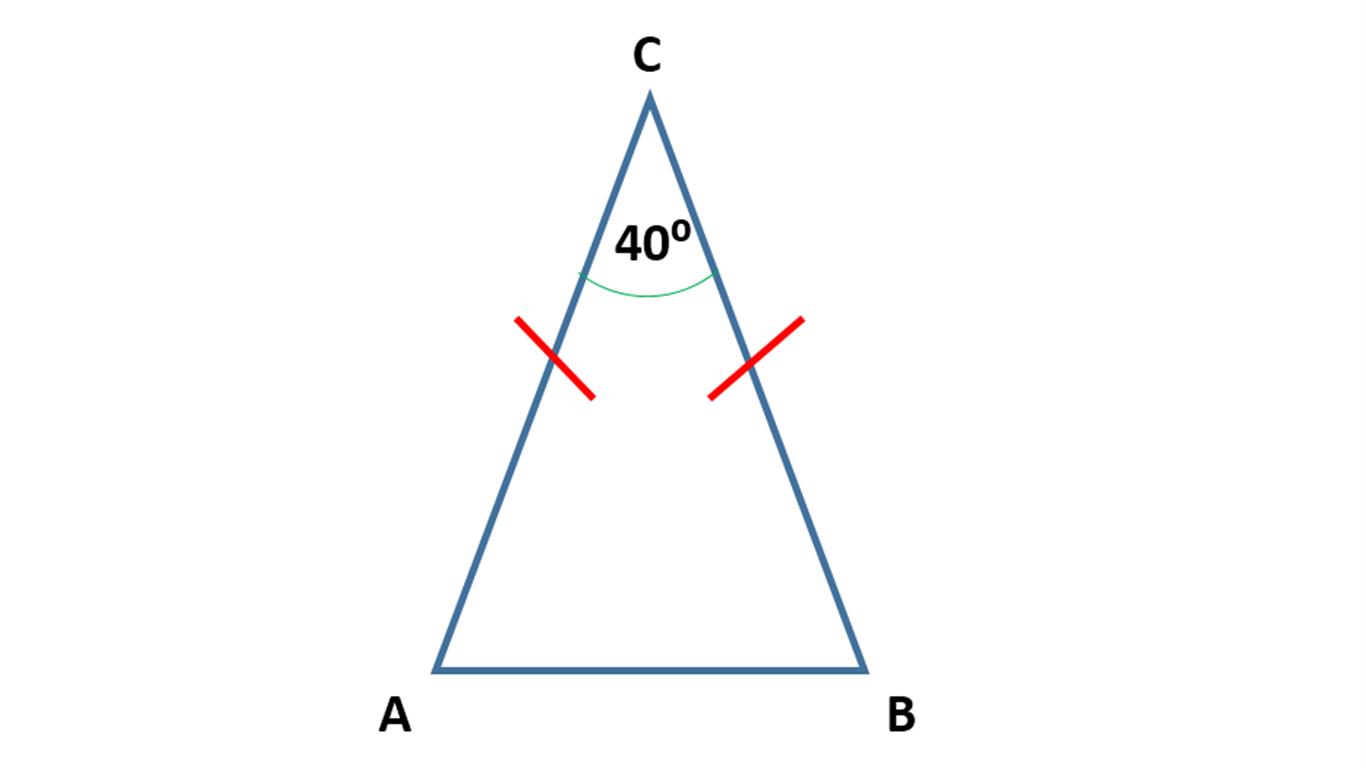
Panjang AC = CB
Sudut ∠A = ∠B
∠A + ∠B + ∠C = 1800
K = AB + BC + AC
3. Segitiga Siku-siku
Segitiga siku-siku merupakan segitiga yang mana salah satu dari sudutnya sebesar 900
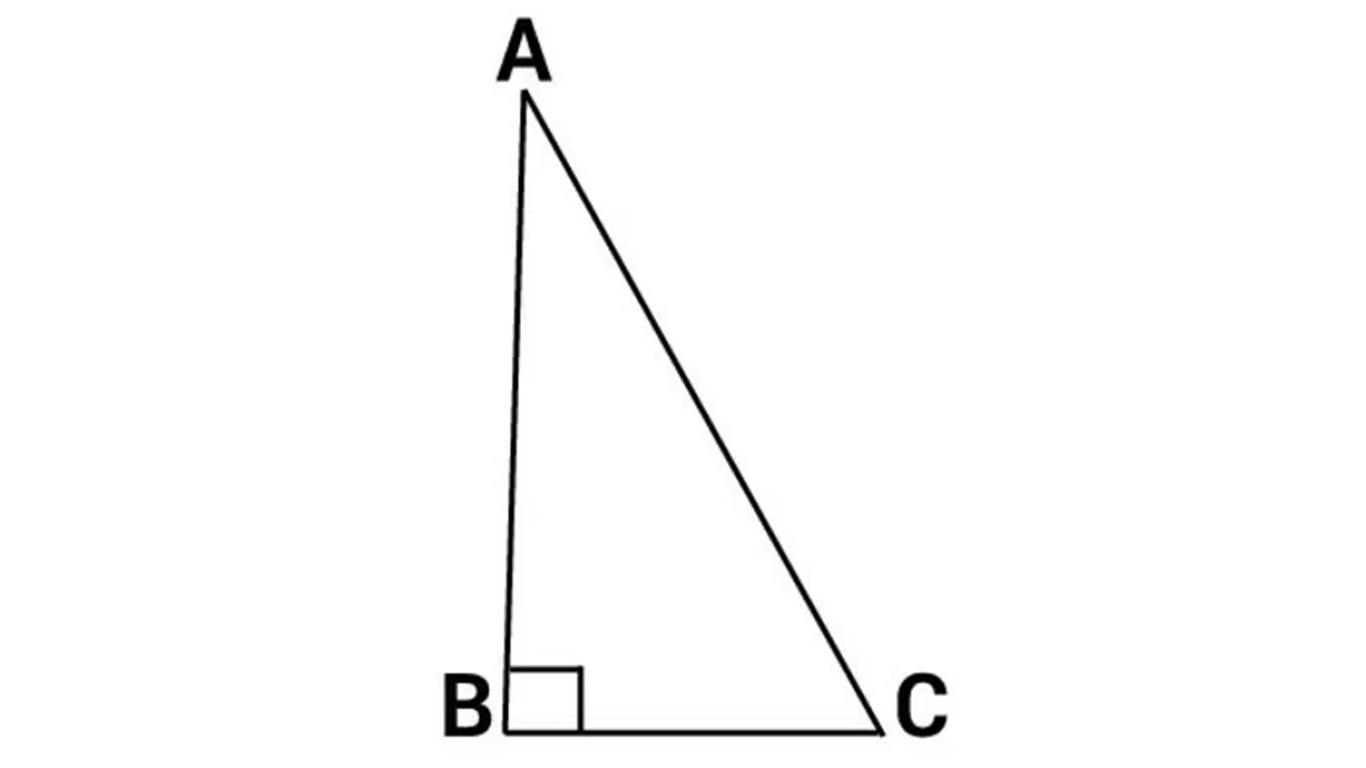
∠A = 900
K = AB + BC + AC
3. Segitiga Sembarang
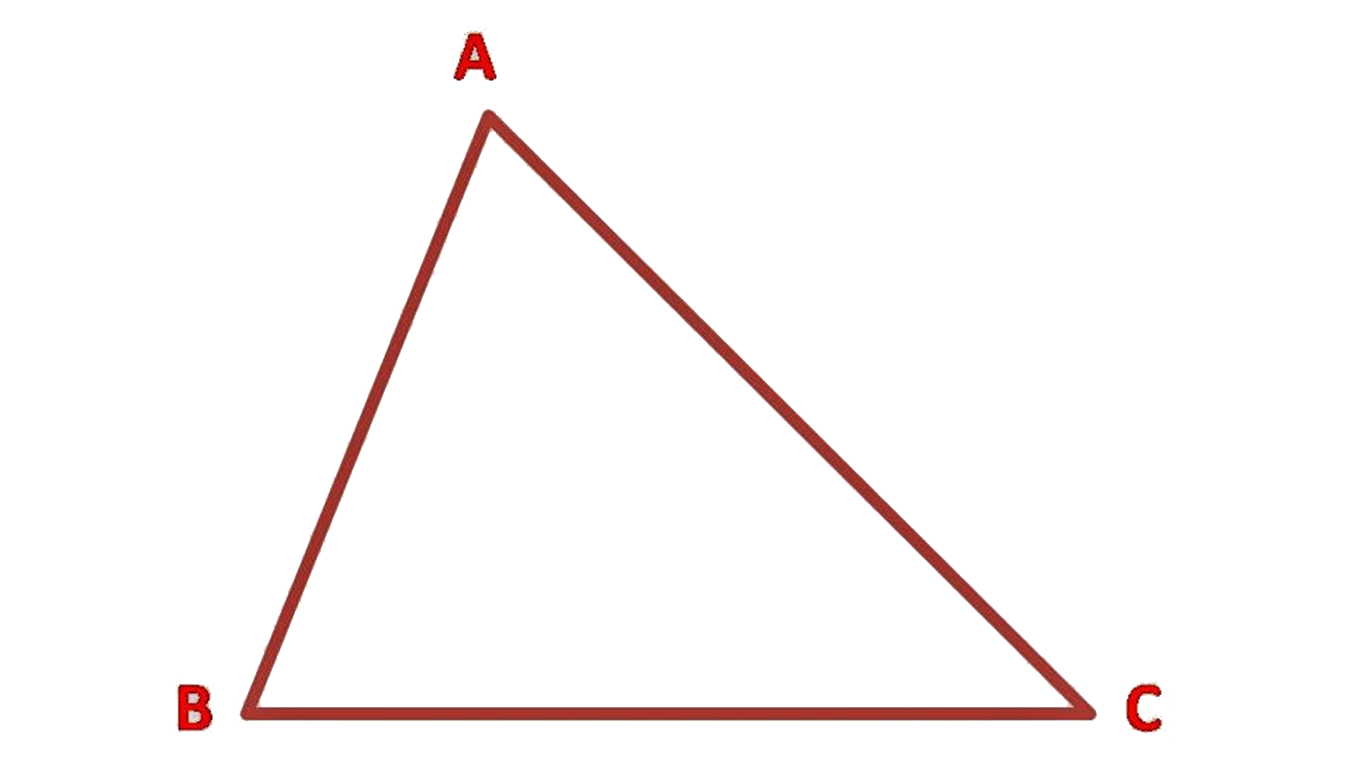
– Ketiga sisinya tidak sama panjang ( AB ≠ BC≠ AC )
– Ketiga sudutnya tidak sama besar (∠A ≠ ∠B ≠ ∠C )
– ∠A +∠B +∠C = 1800
K = AB + BC + AC
Rumus yang biasa digunakan adalah:
L = 1/2.(AB) . (CD)
L = 1/2.a.t
Contoh soal:
1. Tentukan keliling dari suatu segitiga yang memiliki sisi 6 cm!
2. Tentukan luas dari suatu segitiga yang memiliki panjang alas 8 cm serta tingginya 4cm!
Jawab:
- K = 3s
= 3.6
= 18 cm
- L = .a.t
= .8.4
=16 cm2
4. Jajaran Genjang
Jajaran Genjang merupakan sebuah bangun yang memiliki dua pasang sisi yang saling sejajar.
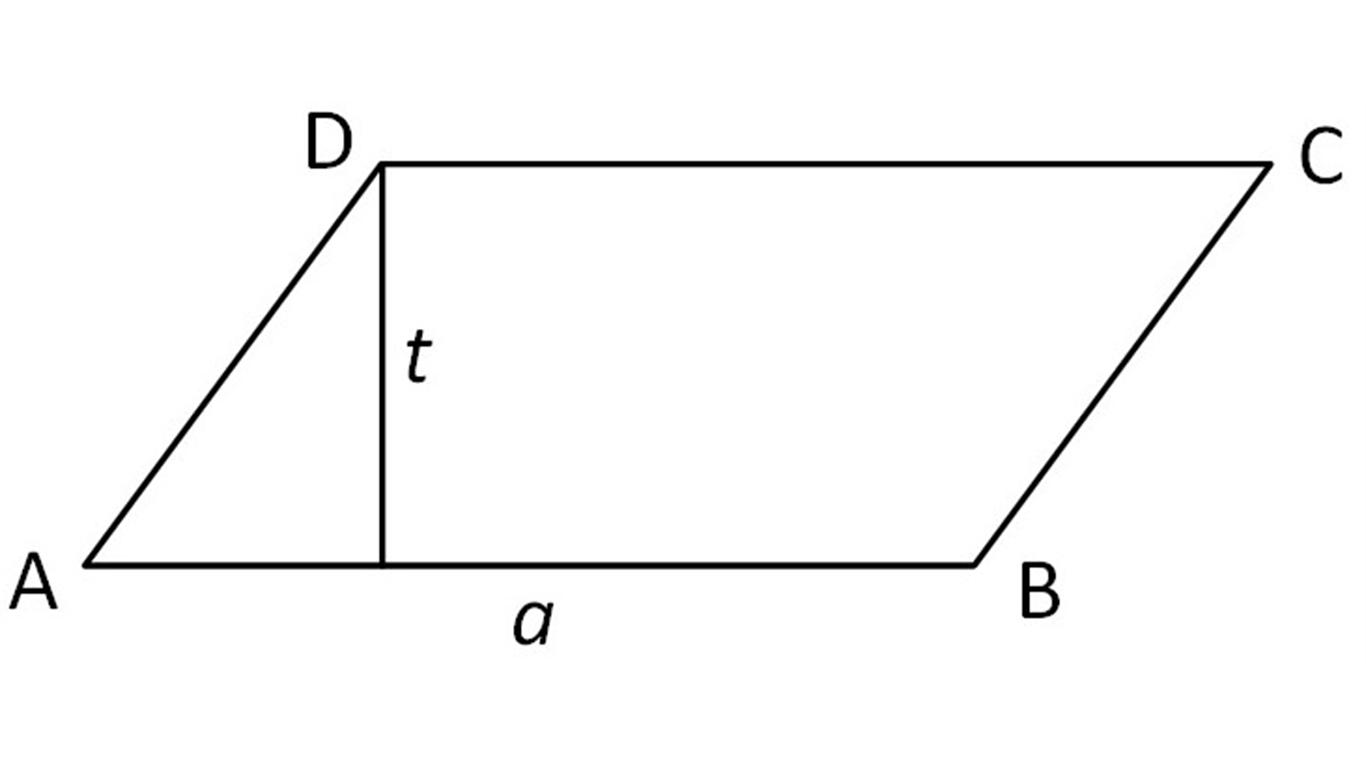
K = AB + BC + CD + DA
Rumus yang biasa digunakan adalah:
K = 2(p + l)
L = alas . tinggi
Contoh soal:
Tentukan keliling dan juga luas dari sebuah jajaran genjang yang memiliki panjang alas 6 cm, lebar 4 cm dan tinggi 3 cm!
Jawab:
K = 2(p + l)
= 2(6 + 4)
= 2(10)
= 20 cm
L = a.t
= 6 x 3
= 18 cm2
5. Layang-layang
Layang-layang merupakan suatu bangun dengan dua pasang sisinya yang sama panjang.
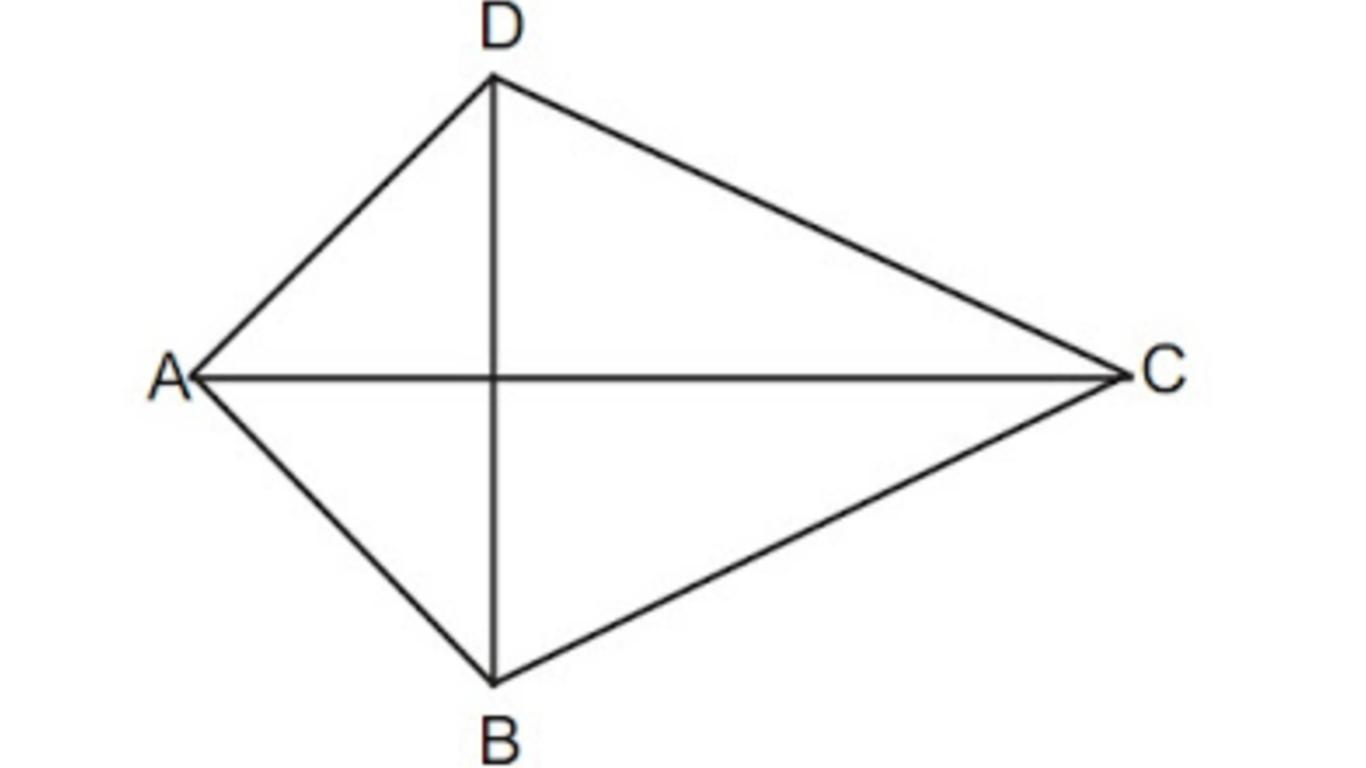
Rumus yang biasa digunakan adalah:
K (Kll) = AB + BC + CD + DA
L = 1/2.d1.d2
Diagonal 1 (d1) = d1 = 2 × L ÷ d2
Diagonal 2 (d2) = d2 = 2 × L ÷ d1
a atau b = a = (½ × Kll) – c
c atau d = c = (½ × Kll) – a
Contoh soal:
Tentukan luas dari sebuah layang-layang yang mempunyai panjang diagonal 9 cm dan lebar diagonal 8 cm!
Jawab:
L = 1/2.d1.d2
= . 8 . 9
= 36 cm2
6. Trapesium
Trapesium hanya mempunyai sepasang sisi yang sejajar.
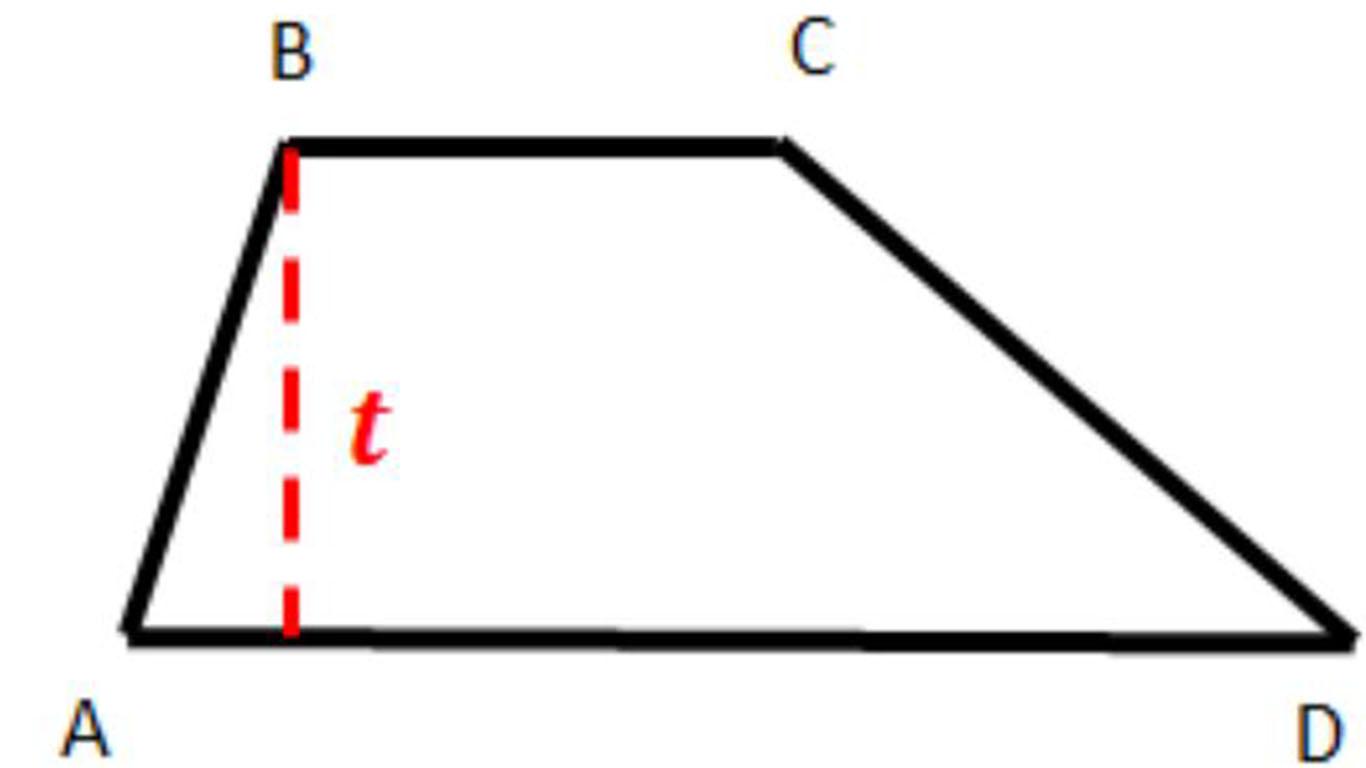
Rumus yang biasa digunakan adalah:
K = AB + BC + CD + DA
L = 1/2.t.(AB + CD)
Contoh soal:
Tentukan luas dari sebuah trapesium yang mempunyai P1 = 8 cm, P2 = 13 cm dan tinggi 6 cm!
Jawab:
L = 1/2.t.(P1 + P2)
= 1/2. 6 . (8 + 13)
= 63 cm2
7. Lingkaran
Bentuk lingkaran diperoleh dengan menentukan tempat kedudukan atau himpunan semua titik-titik yang berjarak tetap terhadap sebuah titik.
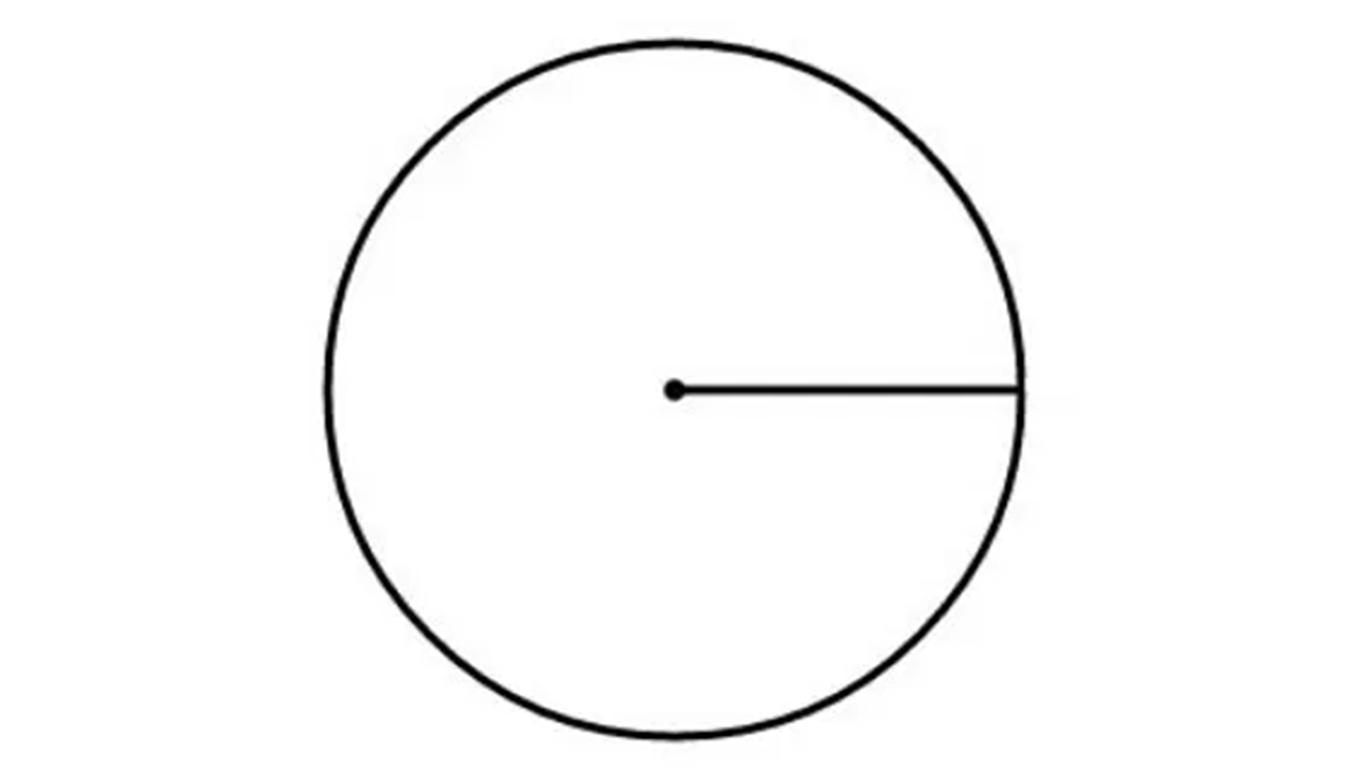
Rumus yang biasa digunakan adalah:
K = 2π r
L = π r2
Contoh : Tentukan keliling dan luas dari sebuah lingkaran yang mempunyai diameter 60 cm!
Jawab:
K = 2.π .r
= 2. π . 30
= 60p cm2
L = π r2
= π .302
= 900π cm2
Demikianlah ulasan singkat mengenai Geometri Bidang Datar yang dapat kami sampaikan. Semoga ulasan di atas mengenai Geometri Bidang Datar dapat kalian jadikan sebagai bahan belajar kalian.
Satu pemikiran pada “Geometri Bidang Datar”