Matriks atau elemen matriks merupakan sekumpulan bilangan yang disusun secara baris atau kolom atau kedua-duanya serta diletakan di dalam tanda kurung.
Berbagai bialgan yang membentuk suatu matriks disebut sebagai elemen-elemen matriks. Matriks dipakai guna menyederhanakan penyampaian data, sehingga akan lebih mudah untuk diolah.
Matriks merupakan sekumpulan bilangan yang telah disusun secara baris dan kolom serta telah ditempatkan di dalam kurung biasa atau kurung siku. -wikipedia
Contoh mudah untuk mengetahui matriks, kalian dapat melihat ilustrasi yang ada di bawah ini:
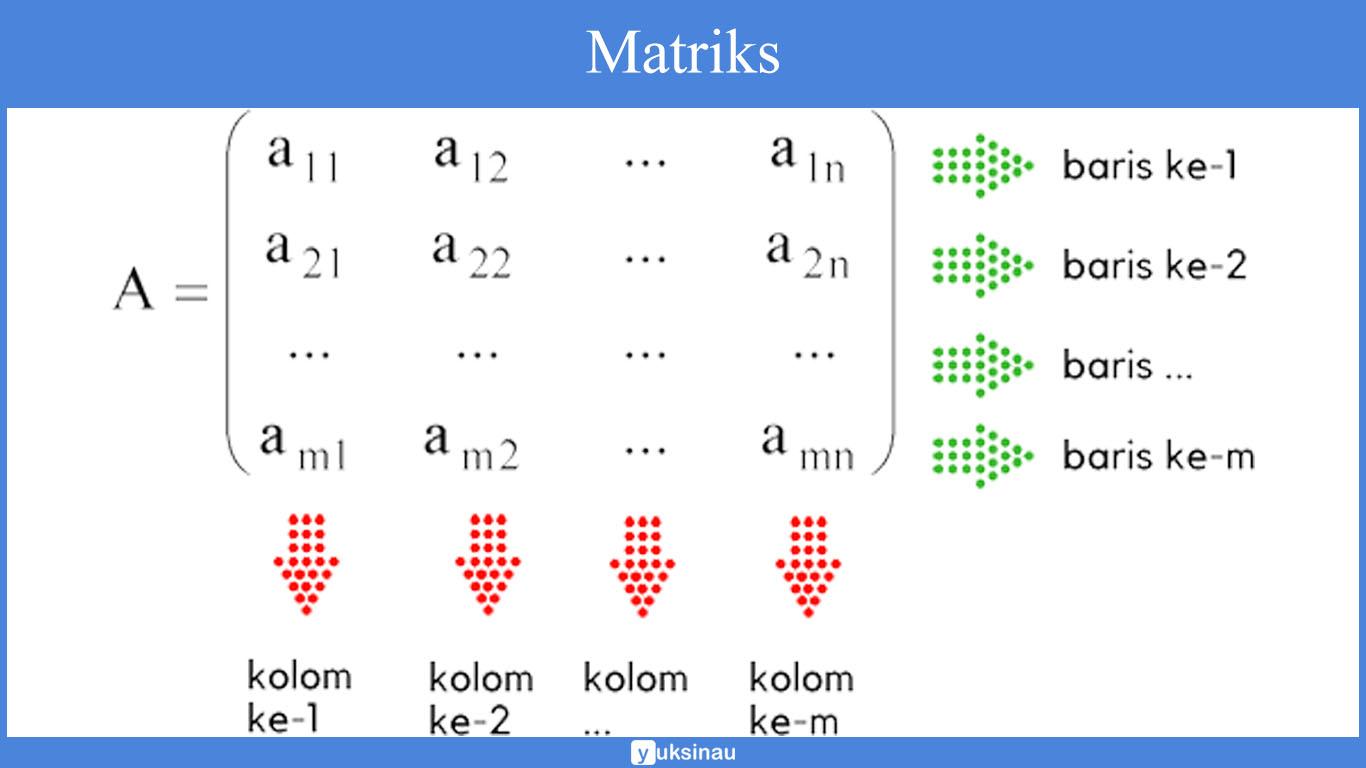
Ilustrasi di atas bisa kalian baca dengan pemahaman seperti ini:
- a11 dibaca sebagai baris ke-1 dan kolom ke-1
- a12 dibaca sebagai baris ke-1 dan kolom ke-2;
- amn yang artinya baris ke-m dan kolom ke-n.
Banyaknya baris dan kolom dalam matriks disebut sebagai ordo.
Urutan yang perlu untuk kalian ingat adalah baris lalu kolom. Matriks dalam ilustrasi di bawah ini mempunyai ordo 2×3. Hal tersebut disebabkan matriks tersebut mempunyai dua baris dan tiga kolom.
Untuk mengetahui matriks dalam matematika lebih dalam, terdapat beberapa jenis matriks yang perlu untuk kalian ketahui. Berikut jenis-jenis matriks yang ada di matematika:
- Matriks nol : matriks yang seluruh elemennya merupakan nol.
- Matriks baris : matriks yang hanya mempunyai satu baris.
- Matriks kolom : matriks yang hanya mempunyai satu kolom.
- Matriks persegi : matriks yang mempunyai jumlah baris dan kolom yang sama.
- Matriks identitas : matriks konstanta dengan elemen diagonal utama merupakan 1.

Selain beberapa jenis matriks di atas, terdapat juga matriks yang disebut sebagai transpose matriks.
Kalian ngat ‘kan jika matriks selalu dilambangkan dengan huruf kapital?
Sebagai contoh lambang satu matriks adalah A.
Nah, transpose dari matriks A akan dilambangkan dengan A’ (dengan tanda petik satu di atasnya).
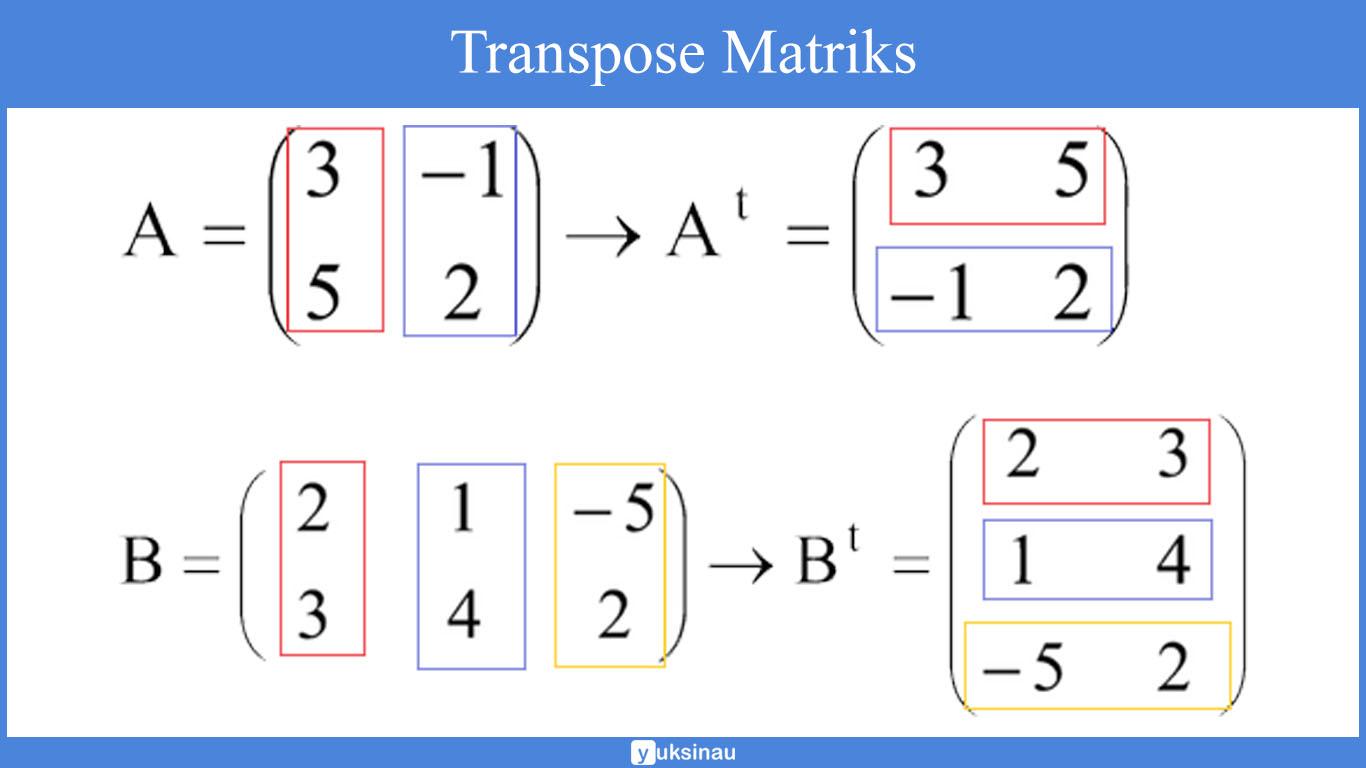
Transpose sendiri digunakan dengan meletakkan baris pada matriks A yang dijadikan kolom pada matriks A’, begitu pun sebaliknya.
Berikut contoh dari transpose matriks:
Daftar Isi
Matriks
Sebagai contoh, akan kami berikan data pada kehidupan sehari-hari yang dapat kita oleh dengan menggunakan matriks.
Contoh:
Diketahui jumlah penjualan mobil jenis A, B, dan C, dengan harga jual pada masing-masing mobil adalah 146, 275, dan 528 (dalam juta) pada kota-kota P, Q, R, yaitu:
| JENIS MOBIL | HARGA MOBIL (JUTA) | JUMLAH PENJUALAN TIAP KOTA (UNIT) | ||
| KOTA P | KOTA Q | KOTA R | ||
| A | 146 | 34 | 56 | 41 |
| B | 275 | 45 | 36 | 37 |
| C | 528 | 51 | 32 | 46 |
Data penjualan dari mobil tersebut bisa kita tulis ke dalam bentuk matriks dengan bentuk seperti berikut ini:
- Matriks harga mobil yaitu:

- Matriks jumlah penjualan yaitu:

Bagaimana? Jadi lebih sederhana kan?
Ordo Matriks
Pada penjelasan di atas, matriks terdiri dari beberapa unsur yang tersusun secara baris dan kolom.
Apabila banyak baris pada sebuah matriks ialah m, serta banyak kolom pada suatu matriks adalah n, maka matriks tersebut mempunyai ordo matriks atau ukuran m x n.
Perlu kalian bahwa m dan n hanya suatu notasi, sehingga tidak diperkenankan untuk dilakukan sebuah perhitungan (penjumlahan, perkalian).
Pada contoh matriks jumlah penjualan mobil di atas diketahui bahwa:
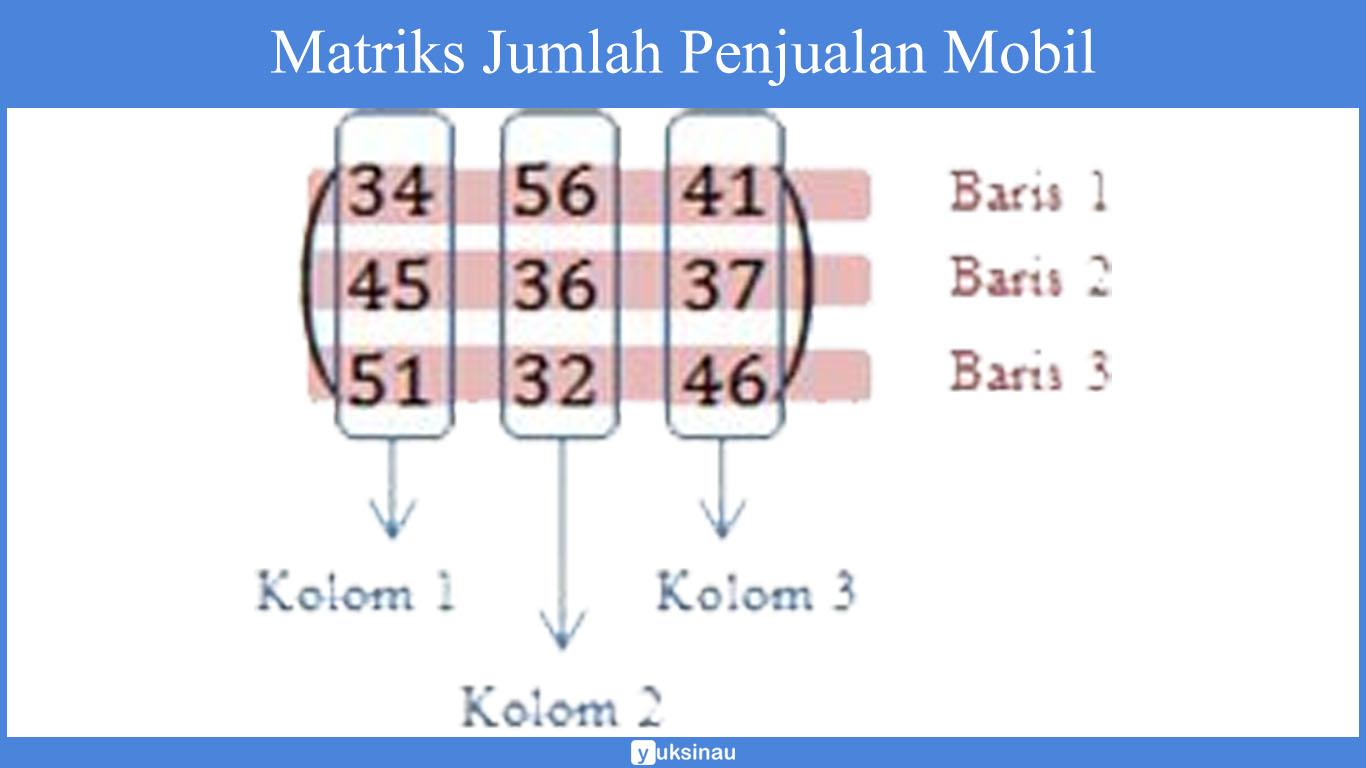
- Banyak baris, m = 3
- Banyak kolom, n = 3
- Ordo matriks, m x n = 3 x 3
Penamaan atau notasi matriks dengan memakai huruf kapital. Sementara pada elemen di dalamnya menggunakan huruf kecil sesuai dengan penamaan matriks serta diberi indeks ij.
Indeks tersebut menyatakan seabgai posisi elemen matriks. Yakni di baris i dan kolom j. Contohnya, matriks sebelumnya untuk matriks penjualan mobil:

Di mana, e12 = 56 merupakan elemen matriks yang terletak di baris ke-1 (i = 1). Serta kolom ke-2 (j = 2). Begitu pula dengan elemen matriks yang lainnya.
Di dalam amteri matriks juga ada dua jenis diagonal, yakni diagonal utama dan diagonal sekunder.
Diagonal utama adalah berbagai elemen yang dapat membentuk garis miring.
Sedangkan untuk diagonal sekunder adalah kebalikan dari garis miring diagonal utama.
Perhatikan gambar matriks berikut:

Diagonal utamanya yaitu elemen 34, 36, 46, sementara untuk diagonal sekundernya yaitu elemen 41, 36, 51.
Matriks Identitas
Matriks diagonal dengan berbagai elemen diagonal utamanya memiliki nilai 1 yang disebut sebagai matriks identitas.
Pada umumnya matriks identitas akan dinotasikan dengan “I”. Misalnya:

Jenis-jenis Matriks
Seperti yang telah kami sebutkan di atas, ada beberapa jenis metrik. Namun kali ini kita akan membahas jenis matriks berdasarkan pada jumlah baris dan kolom dan juga pola elemen matriksnya. Diantaranya adalah sebagai berikut:
1. Matriks Baris dan Matriks Kolom
Matriks baris merupakan sebuah matriks yang hanya mempunyai satu baris saja. Sementara untuk matriks kolom merupakan sebuah matriks yang hanya mempunyai satu kolom saja.
Sebagai contoh:
A = (1 4) atau B = (3 7 9) merupakan matriks baris

2. Matriks Persegi
Matriks persegi merupakan matriks yang mempunyai jumlah kolom dan juga baris yang sama. Matriks persegi mempunyai ordo n.
Sebagai contoh:
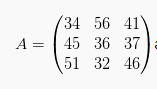 merupakan matriks persegi berordo 3. Atau
merupakan matriks persegi berordo 3. Atau
![]() merupakan matriks persegi berordo 2.
merupakan matriks persegi berordo 2.
3. Matriks Segitiga Atas dan Segitiga Bawah
Matriks segitiga atas merupakan persegi A yang mana mempunyai elemen matriks aij = 0 untuk i > j atau elemen-elemen matriks di bawah diagonal utama yang bernilai 0.
Sementara matriks segitiga bawah merupakan matriks persegi A yang mempunyai elemen matiks aij = 0 untuk i < j atau berbagai elemen matriks di atas diagonal utama yang nilainya 0.
Sebagai contoh:
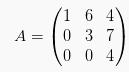 berikut merupakan matriks segitiga atas. Sedangkan
berikut merupakan matriks segitiga atas. Sedangkan
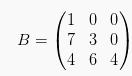 berikut merupakan matriks segitiga bawah.
berikut merupakan matriks segitiga bawah.
4. Matriks Diagonal
Matriks diagonal merupakan matriks persegi A yang mempunyai elemen matiks aij = 0 untuk i ≠ j atau berbagai elemen matriks di luar diagonal utama yang nilainya 0.
Sebagai contoh:

5. Matriks Skalar
Matriks skalar merupakan matriks diagonal yang mempunyai elemen-elemen pada diagonal utamanya yang bernilai sama.
Sebagai contoh:

6. Matriks Indentitas
Lihat kembali pada penjelasan di atas.
7. Matriks Simetris
Matriks simetris merupakan matriks persegi A yang mempunyai elemen matiks baris ke-I sama dengan elemen matriks kolom ke-j untuk i = j. Atau, bisa kita sebut sebagai elemen aij sama dengan elemen.
Sebagi contoh:

Dapat dilihat bahwa elemen baris ke-1 sama dengan kolom ke-1, baris ke-2 sama dengan kolom ke-2, dan baris ke-3 sama dengan kolom ke-3.
Transpose Matriks
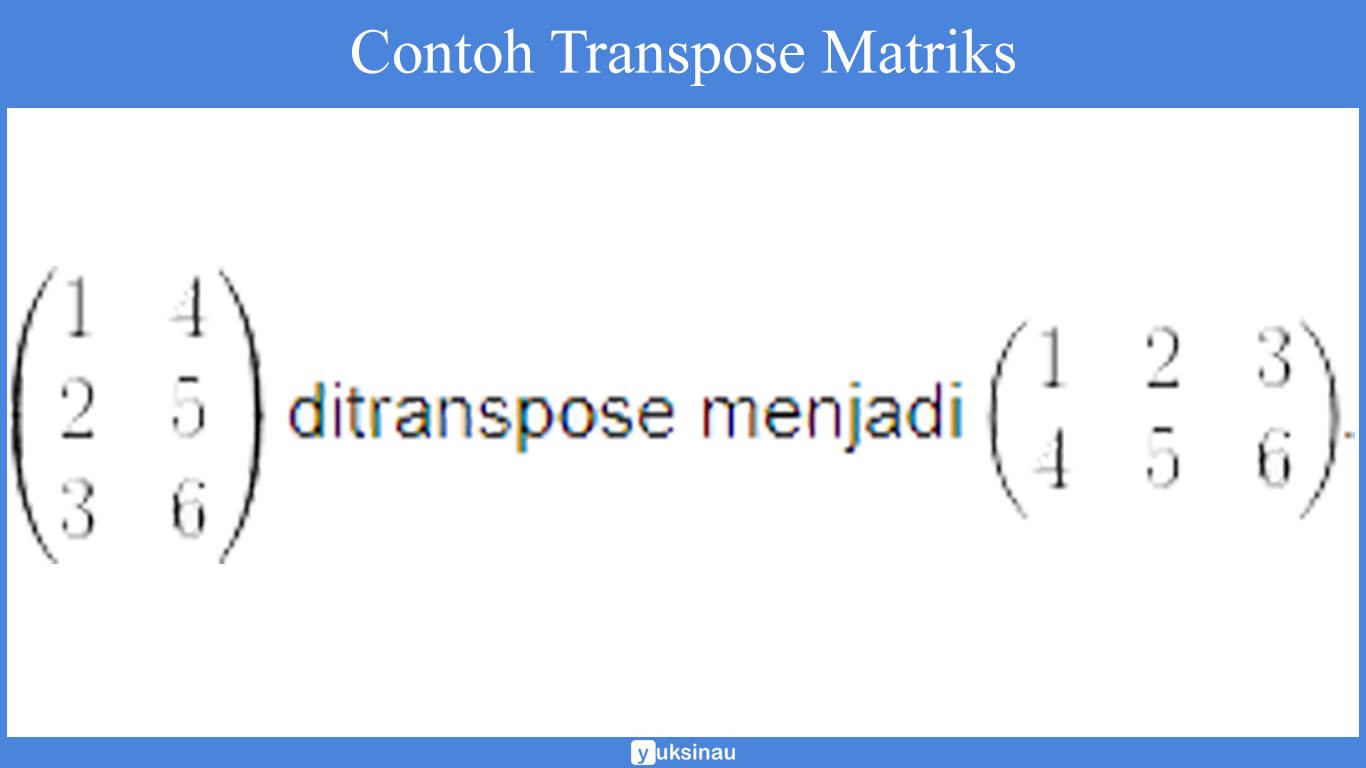
Transpose matriks adalah perubahan baris menjadi kolom dan begitu pula sebaliknya.
Transpose matriks dari Amxn merupakan suatu matriks dengan ukuran (n x m) dan bernotasi AT. Apabila matriks A ditransposekan, maka baris 1 akan menjadi kolom 1, baris 2 menjadi kolom 2, dan begitu pula seterusnya.
Sebagai contoh:
Adapun sifat dari transpose matriks, yaitu: (AT)T = A
Setelah mengetahui secara singkat mengenai matriks, berikut akan kami berikan penjelasan mengenai cara pengoperasian matriks dalam matematika. Yang meliputi penjumlahan, perkalian, determinan, dan invers. Simak baik-baik penjelasan di bawah ini ya.
Penjumlahan dan Pengurangan Matriks
Dua matriks atau lebih, bisa kita jumlhakan hanya apabila matriks tersebut mempunyai ordo yang sama.
Penjumlahan dilakukan dengan cara menjumlahkan elemen-elemen yang letaknya sama. Sebagai contoh:

maka:

Sama halnya dengan yang ada pada penjumlahan, pengurangan matriks bisa kita lakukan dengan hanya apabila terdapat dua matriks atau lebih.
Mempunyai ordo yang sama. Pengurangan dilakukan pada elemen-elemen yang berposisi sama.
Sebagai contoh:

maka:

Adapun sifat dari penjumlahan dan pengurangan pada matriks, antara lain:
- A + B = B + A
- (A + B) + C = A + (B + C)
- A – B ≠ B – A
Perkalian Matriks
Matriks bisa kita kalian dengan menggunakan suatu bilangan bulat atau dengan matriks lain.
Kedua perkalian tersebut mempunyai beberapa syaratnya masing-masing. Berikut penjelasan lengkapnya:
Perkalian Matriks dengan bilangan bulat
Sebuah matriks bisa kita kalian dengan bilangan bulat, maka hasil dari perkalian tersebut dapat berwujud matriks dengan elemen-elemennya yang merupakan hasil kali antara bilangan dengan elemen-elemen matriks tersebut.
Apabila matriks A dikali dengan bilangan r, maka r.A = (r.aij)
Sebagai contoh:
Apabila  serta bilangan r = 2, maka:
serta bilangan r = 2, maka: 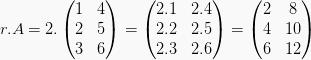
Perkalian matriks dengan bilangan bulat yang dicampur dengan penjumlahan atau pengurangan matriks bisa dilakukan dalam matriks dengan ordo yang sama.
Berikut ada dua sifat perkaliannya, antara lain:
- r(A + B) = rA + rB
- r(A – B) = rA – rB
Perkalian dua matriks
Perkalian antara dua matriks yakni perkalian pada matriks A dan B, bisa kita lakukan apabila jika jumlah kolom A sama dengan jumlah baris B.
Perkalian itu kemudian akan sebuah matriks dengan jumlah baris sama dengan matriks A serta dengan jumlah sama dengan matriks B, sehingga:
gambar
Elemen-elemen matriks C(mxs) adalah penjumlahan dari hasil kali berbagai elemen baris ke-i matriks A dengan kolom ke-j matiks B. Berikut adalah gambar skemanya:
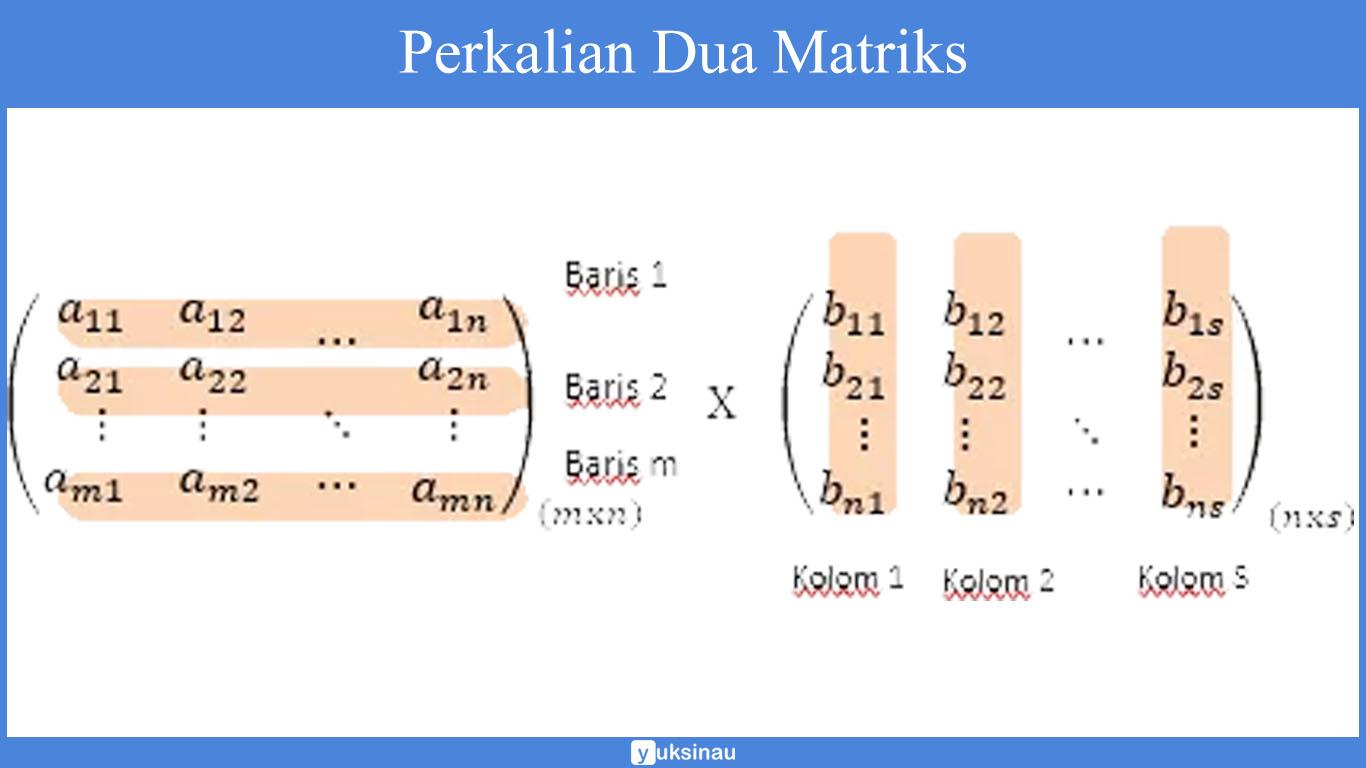
Contohnya matriks A mempunyai ordo (3 x 4) serta matriks B mempunyai ordo (4 x 2), maka matriks C mempunyai ordo (3 x 2).
Elemen C yang ada pada baris ke-2 dan kolom ke-2 atau a22 didapatkan dari jumlah hasil perkalian berbagai elemen baris ke-2 matriks A serta kolom ke 2 matriks B. Sebagai contoh:
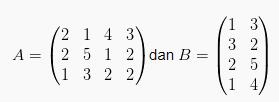
maka:
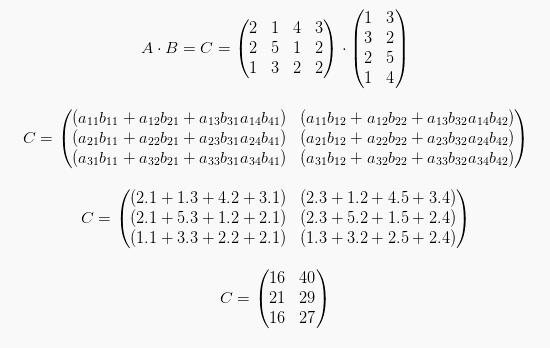
Perlu diingat bahwa sifat dari perkalian dua matriks adalah:
A x B ≠ B x A
Sebagai pembuktian, diketahui: 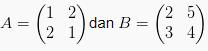 maka:
maka:
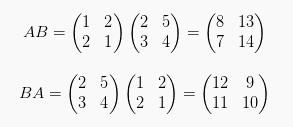
Terbukti bahwa A x B ≠ B x A. Terdapat beberapa sifat lain dari perkalian matriks dengan bilangan atau dengan matriks lain, diantaranya adalah sebagai berikut:
- k(AB) = (kA)B
- ABC = (AB)C = A(BC)
- A(B + C) = AB + AC
- (A + B)C = AC + BC
Determinan Matriks
Determinan dari sebuah matriks A diberi notasi tanda kurung, sehingga penulisannya menjadi |A|. Determinan hanya dapat dilakukan pada matriks persegi.
Determinan matriks ordo 2×2
Apabila ![]() maka determinan A yaitu:
maka determinan A yaitu:
![]()
Determinan matriks ordo 3×3 (aturan Sarrus)
Apabila 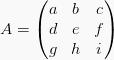 maka determinan A yaitu:
maka determinan A yaitu:
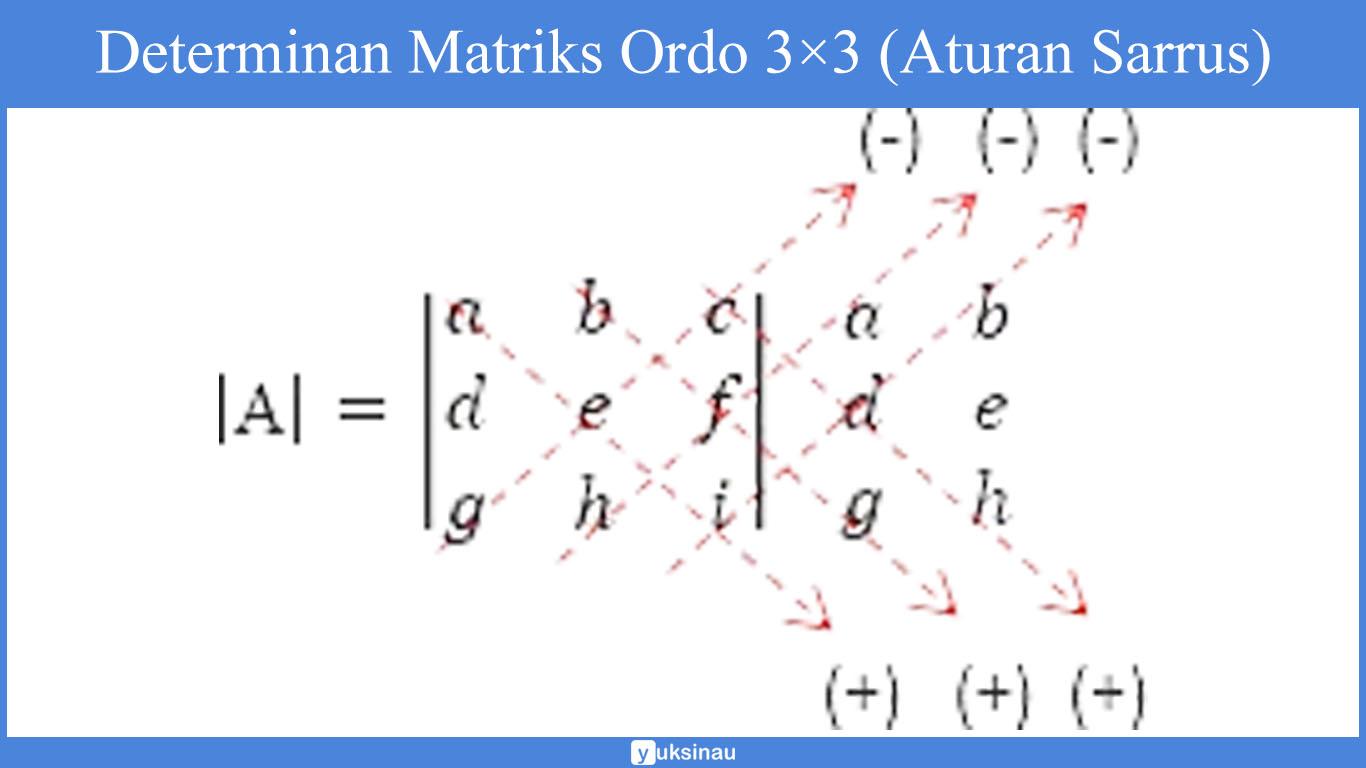
= aei + bfg + cdg – ceg – afh – bdi
Determinan matriks mempunya beberapa sifat seperti berikut ini:
1. Determinan A = Determinan AT
2. Tanda determinan berubah apabila 2 baris/2 kolom yang berdekatan dalam matriks ditukar.
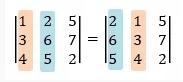
3. Apabila sebuah baris atau kolom pada suatu determinan matriks mempunyai faktor p, maka p bisa dikeluarkan menjadi pengali.

4. Apabila terdapat dua baris atau dua kolom adalah saling berkelipatan, maka nilai determinannya yaitu 0.
![]()
5. Nilai determinan dari matriks segitiga atas atau bawah merupakan hasil kali dari berbagai elemen diagonal saja.
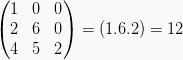
Invers Matriks
Sebuah matrik A mepunyai invers (kebalikan) apabila terdapat matrik B yang bisa membentuk persamaan AB = BA = I, dengan I merupakan matrik identitas.
Invers dari sebuah matriks berordo (2 x 2) seperti ![]() bisa dirumuskan sebagai:
bisa dirumuskan sebagai:
![]()
Invers matrik mempunyai beberapa sifat seperti berikut ini:
- AA-1 = A-1A = I
- (A-1)-1 = A
- (AB)-1 = B-1A-1
- Apabila AX = B, maka X = A-1B
- Apabila XA = B, maka X = BA-1
Contoh Soal Matriks dan Pembahasan
Soal 1.
Ssebuah perkalian matriks ![]() menghasilkan matrik nol. Tentukan nilai x yang memenuhui persamaan tersebut!
menghasilkan matrik nol. Tentukan nilai x yang memenuhui persamaan tersebut!
Jawab:

Maka nilai x yang memenuhi yaitu x1 = 2 dan x2 = 3.
Soal 2.
Apabila terdapat matrik 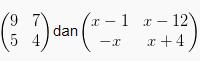 saling invers, tentukan nilai x!
saling invers, tentukan nilai x!
Jawab:
Diketahui bahwa kedua matrik tersebut saling invers, maka akan berlaku syarat AA-1 = A-1A = I.
Maka dari itu:

Sehingga pada elemen baris ke-1 kolom ke-1 mempunyai persamaan:
9(x – 1) – 7x = 1
9x – 9 – 7x = 1
2x = 10
x = 5
Soal 3.
Apabila terdapat matrik 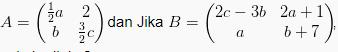 maka supaya A = BT berapakah nilai untuk c?
maka supaya A = BT berapakah nilai untuk c?
Jawab:
Diketahui bahwa A = BT

Sehingga diperoleh 4 persamaan baru dari elemen-elemen matriknya, antara lain:
- 1/2 a = 2 c = 3b (persamaan ke-1)
- 2 = a (persamaan ke-2)
- b = 2a + 1 (persamaan ke-3)
 (persamaan ke-4)
(persamaan ke-4)
Dari persamaan di atas bisa dilakukan substitusi persamaan untuk mendapatkan nilai c, yakni:
a = 2, maka:
b = 2a + 1 = 2(2) + 1 = 5
serta
![]()
Demikianlah ulasan singkat kali ini yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.

Bagus artikelnya, informatif. 🙂
terimakasih atas ilmunya