Sebelum kita membahas mengenai bilangan bulat, sebaiknya kita mengetahui terlebih dahulu apa itu himpunan dan bilangan.
Daftar Isi
Himpunan
Seperti yang telah kami bahas pada artikel sebelumnya, himpunan merupakan suatu kumpulan benda atau objek yang dapat diartikan dengan jelas, sampai kita bisa dengan tepat mengetahui objek yang termasuk himpunan serta yang tidak termasuk dalam himpunan tersebut.
Sebuah Himpunan Matematika biasanya dilambangkan dengan menggunakan huruf kapital seperti: A, B, C, D, E, …………….. Z, benda maupun objek yang termasuk kedalam himpunan disebut anggota himpunan. Serta elemen himpunan ditulis dengan menggunakan sepasang kurung kurawal {……..}
Adapun jenis-jenis dari himpunan, antara lain:
- Himpunan Matematika Semesta
- Himpunan Matematika Kosong
- Himpunan Matematika Bagian
- Himpunan Matematika Sama (Equal)
- Himpunan Matematika Lepas
- Himpunan Matematika Komplemen (Complement set)
- Himpunan Matematika Ekuivalen (Equal Set)
Bilangan
Yang dimaksud sebagai bilangan merupakan sebuah konsep dalam bidang matematika yang dipakai sebagai pencacahan dan pengukuran.
Macam-macam Bilangan
Berikut akan kami berikan macam-macam bilangan dalam matematika, antara lain:
1. Bilangan Asli
Bilangan asli merupakan suatu himpunan bilangan bulat positif yang bukan nol.
Bilangan asli juga memiliki nama lain yakni bilangan hitung atau bilangan yang memilkinilai positif (integer positif).
Sebagai contoh:
{1, 2, 3, 4, 5, 6, 7, 8, 9, …}
2. Bilangan Cacah
Bilangan cacah merupakan suatu himpunan bilangan asli ditambah dengan nol.
Sebagai contoh:
{0, 1, 2, 3, 4, 5, 6, 7, 8, …}
3. Bilangan Negatif
Bilangan negatif atau juga disebut sebagai integer negatif merupakan suatu bilangan yang lebih kecil/ kurang dari nol. Atau juga dapat disebut sebagai bilangan yang letaknya disebelah kiri nol pada garis bilangan.
Sebagai contoh:
{-1, -2, -3, -4, -5, -6, -7, -8, -9, …}
4. Bilangan Bulat
Merupakan bilangan yang terdiri atas bilangan asli, bilangan nol serta bilangan negatif.
Sebagai contoh:
{-4, -3, -2, -1, 0, 1, 2, 3, 4, …}
5. Bilangan Prima
Bilangan prima merupakan bilangan asli lebih besar dari 1 yang faktor pembaginya adalah 1 dan juga bilangan itu sendiri.
Sebagai contoh:
{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …}
6. Bilangan Komposit
Bilangan komposit merupaan suatu bilangan asli lebih besar dari 1 yang bukan merupakan bilangan prima.
Bilangan komposit bisa juga disebut dengan faktorisasi bilangan bulat, atau hasil perkalian dua bilangan prima atau lebih.
Atau juga bisa disebut sebagai bilangan yang memiliki faktor lebih dari dua.
Sebagai contoh:
{4, 6, 8, 9, 10, 12, 14, 15, 16, 18, …}
7. Bilangan Kompleks
Bilangan kompleks merupakan sebuah bilangan yang di mana merupakan penjumlahan antara bilangan real dan bilangan imajiner atau bilangan yang berbentuk a + bi.
Di mana a dan b merupakan bilangan real, serta i merupakan bilangan imajiner tertentu.
Bilangan real a juga disebut sebagai bagian real dari bilangan kompleks. Serta bilangan real b disebut sebagai bagian imajiner.
Apabila dalam sebuah bilangan kompleks, nilai b merupakan 0, maka bilangan kompleks tersebut menjadi sama dengan bilangan real a.
Sebagai contoh:
{3 + 2i}
8. Bilangan Imajiner
Bilangan imajiner merupakan suatu bilangan yang memiliki sifat i2 = −1.
Bilangan ini adalah bagian dari bilangan kompleks. Secara definisi, bilangan imajiner i ini didapatkan dari penyelesaian persamaan kuadratik:
x2 + 1 = 0
atau secara ekuivalen
x2 = -1
atau juga sering dituliskan dengan:
x = √-1
9. Bilangan Real
Bilangan real atau bilangan riil menyatakan bilangan yang bisa kita tuliskan ke dalam bentuk decimal, seperti 2,86547… atau 3.328184.
Dalam notasi penulisan bahasa Indonesia, bilangan desimal merupakan bilangan yang mempunyai angka di belakang koma “,”.
Sementara menurut notasi ilmiah, bilangan desimal merupakan bilangan yang mempunyai angka di belakang tanda titik “.”.
Bilangan real mencangkup bilangan rasional, seperti 42 dan −23/129, serta bilangan irrasional.
Seperti pada π dan √2, serta bisa direpresentasikan sebagai salah satu titik dalam garis bilangan.
Himpunan semua bilangan riil dalam matematika dilambangkan dengan menggunakan huruf R (berasal dari kata “real”).
10. Bilangan Irrasional
Bilangan irrasional adalah suatu bilangan real yang tidak dapat dibagi atau lebih tepatnya hasil baginya tidak pernah berhenti. Sehingga tidak dapat dinyatakan dengan a/b.
Sebagai contoh:
π = 3,141592653358……..
√2 = 1,4142135623……..
e = 2,71828281284590…….
11. Bilangan Rasional
Bilangan rasional merupakan berbagai bilangan yang merupakan rasio (pembagian) dari dua angka (integer) atau bisa dinyatakan dengan a/b.
Yang mana a adalah himpunan bilangan bulat serta b adalah himpunan bilangan bulat namun tidak sama dengan nol.
Bilangan Rasional biasanya diberi lambang Q (yang berasal dari bahasa Inggris “quotient”).
Sebagai contoh:
{½, ⅓, ⅔, ⅛, ⅜, ⅝, ⅞, …}
Bilangan pecahan juga termasuk sekumpulan bilangan rasional. Pecahan desimal merupakan pecahan-pecahan dengan bilangan penyebut 10, 100, dst. { 1/10, 1/100, 1/1000 }.
Seluruh bilangan ini bisa kita temukan pada garis-garis bilangan.
Sebuah bilangan asli bisa dinyatakan dalam bentuk bilangan rasional.
Sebagai contoh:
bilangan asli 2 bisa dinyatakan sebagai 12/6 atau 30/15 dan sebagainya.
12. Bilangan Pecahan
Bilangan pecahan merupakan suatu bilangan yang disajikan atau ditampilkan dalam bentuk a/b. Di mana a, b merupakan bilangan bulat dan b ≠ 0. a disebut sebagai pembilang serta b disebut sebagai penyebut.
Bilangan Bulat
Merupakan himpunan yang terdiri atas bilangan bulat negatif, nol dan positif. Selain itu juga meliputi bilagan cacah, bilangan prima, bilangan asli, bilangan nol, bilangan serta bilangan komposit dan tidak meliputi bilangan imajiner, irrasional serta pecahan.
Bilangan ini biasanya di lambangkan dengan penggunaan huruf ‘Z’ yang berasal dari Bahasa jerman yakni ‘Zahlen’ yang artinya bilangan.
Berikut ini merupakan garis bilangan yang terdiri dari bilangan bulat positif, nol, bilangan cacah, serta negatif.
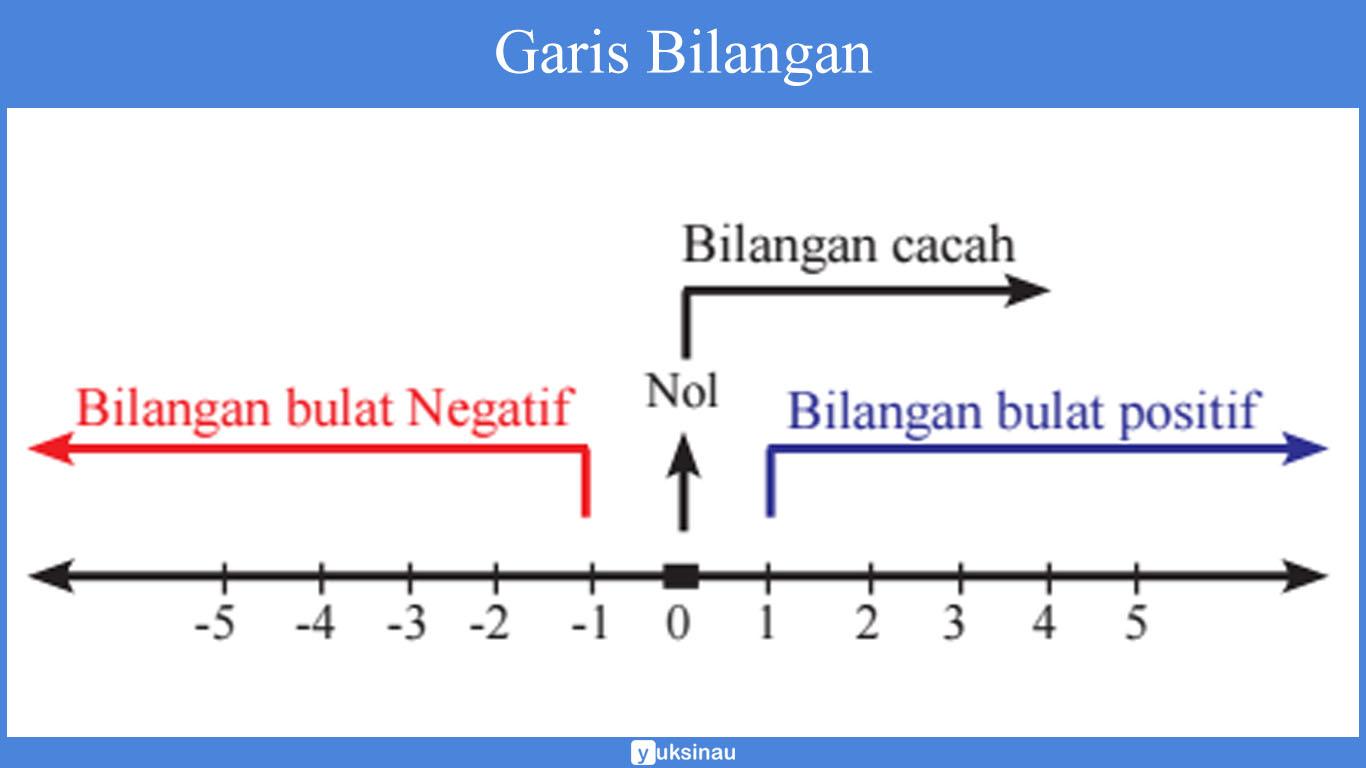
Untuk lebih memahami pengertian dari bilangan bulat, silahkan perhatikan gambar struktur bilangan di bawah ini.
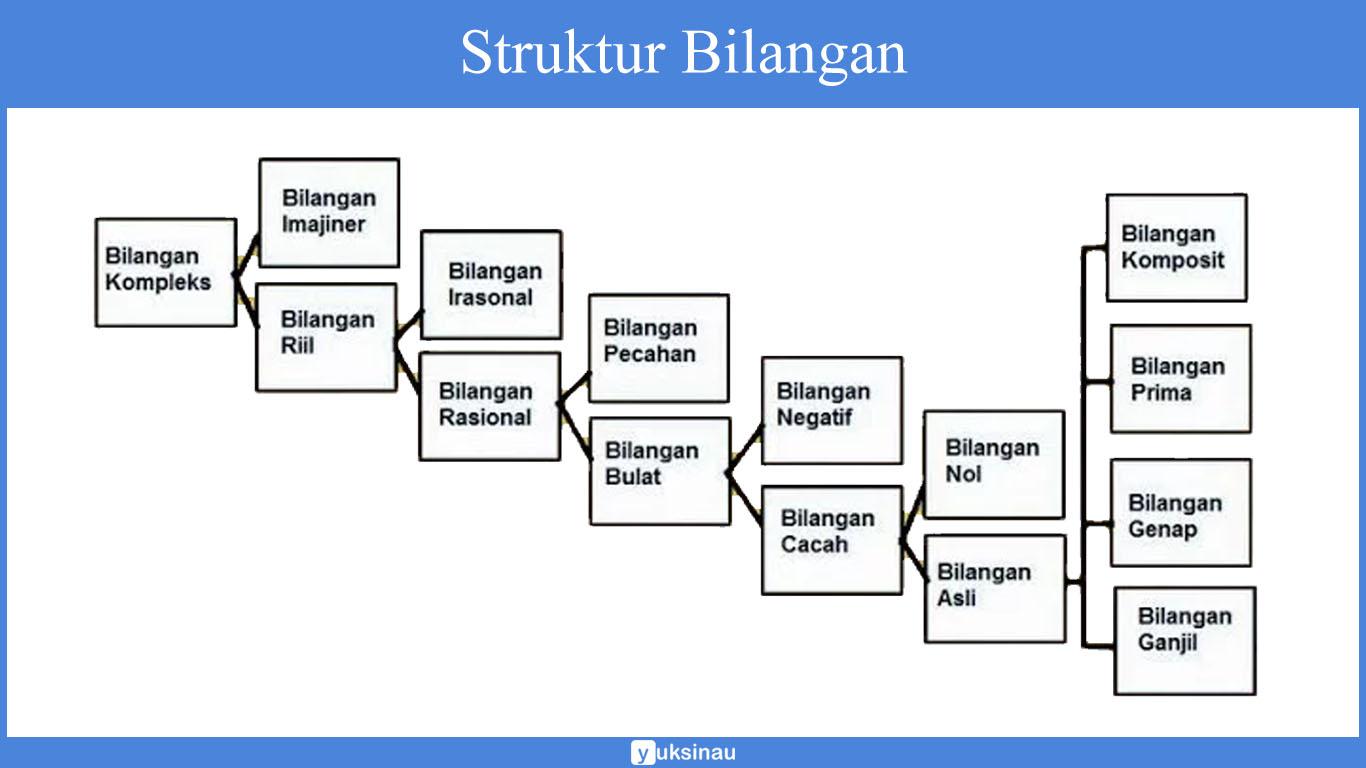
Dari gambar skema di atas, bisa kita lihat bahwa bilangan bulat termasuk ke dalam bilangan rasional yang mana adalah bagian dari bilangan real. Selain itu, bilangan ini juga terdiri atas:
- Bilangan bulat negatif = {…,–5,–4,–3,–2,–1}
- Bilangan nol = {0}
- Bilangan asli atau bilangan bulat positif = {1,2,3,4,5,…} yang dibagi lagi menjadi:
- Bilangan ganjil = {1,3,5,7,…}
- Bilangan genap = {2,4,6,8,…}
Nah, berikut ini adalah uraian atau penjelasan dari macam-macam bilangan bulat yang wajib untuk kaian ketahui, diantaranya yaitu:
1. Bilangan Positif
Bilangan bulat positif merupakan seluruh semua bilangan bulat di sebelah kanan garis bilangan yang dibatasi oleh angka nol.
Sebagai contoh: 1, 2, 3, 4, dst.
Bilangan positif juga terbagi menjadi dua macam, yakni bilangan ganjil serta bilangan genap.
Bilangan Ganjil
Bilangan ganjil merupakan bilangan positif yang tidak habis dibagi 2.
Contoh: 1, 3, 5, 7, dst.
Bilangan Genap
Bilangan genap merupakan bilangan positif yang habis dibagi 2.
Contoh: 2, 4, 6, dst.
Catatan: Nol dan juga bilangan asli membentuk sistem bilangan cacah, {0, 1, 2, 3, …}.
2. Bilangan Negatif
Bilangan negatif merupakan suatu bilangan yang terletak di sebelah kiri 0 (nol) pada garis bilangan bulat.
Bilangan negatif bilangan yang bernilai negatif, di mulai dari -1, -2, -3, -4, -5 dan seterusnya. Dan bilangan negeatif lebih dari sama dengan -1 (>=-1).
3. Bilangan 0 (Nol)
Nol bukan merupakan bilangan positif maupun bilangan negatif dan juga Nol.
Contoh Soal:
- Suhu Kota Banjarneara pada hari Senin 25 Juni 2018 mencapai 240 celsius sementara di di hari Jumat mencapai 200 Celsius.
Angka 24 dan 20 disini merupakan bilangan bulat positif. - BMKG tengah mengukur dalamnya laut. Apabila disebutkan dalam laut x 30 meter dari permukaan laut. Maka di angka yang di tulis merupakan -30 meter.
Angka -30 tersebut merupakan bilangan bulat negatif. - Dalam suatu kebun binatang terdapat banyak sekali jumlah hewan. Seorang anak akan di berikan tugas untuk menghitung jumlah burung yang terdapat di dalam kebun binatang tersebut. Setelah di hitung ternyata banyaknya jumlah burung ada sebanyak 35 burung.
Angka 35 merupakan bilangan bulat positif.
Sifat-sifat Bilangan Bulat
Berikut adalah sifat-sifat bilangan bulat, antara lain:
| Sifat | Penambahan | Perkalian |
| Tertutup | a + b = merupakan bilangan bulat | a × b = merupakan bilangan bulat |
| Asosiatif | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) × c |
| Komutatif | a + b = b + a | a × b = b × a |
| Memiliki unsur identitas | a + 0 = a | a × 1 = a |
| Setiap bilangan memiliki invers | a + (−a) = 0 | Tidak punya |
| Distributif | a × (b + c) = (a × b) + (a × c) | |
| Tidak ada pembagi nol | – | apabila a × b = 0, maka a = 0 atau b = 0 (atau keduanya) |
Keterangan:
Tertutup: operasi perkalian dan juga penjumlahan bilangan bulat akan menghasilkan bilangan bulat.
Tidak ada pembagi nol: pembagian bilangan bulat dengan nol akan menghasilkan nilai tidak terdefinisi (∞).
Asosiatif: penjumlahan ataupun perkalian dari tiga buah bilangan bulat yang dikelompokkan secara berbeda akan memiliki hasil yang sama.
Komutatif: pertukaran letak angka pada penjumlahan dan juga perkalian bilangan bulat memiliki hasil yang sama.
Sebagai contoh:
1 + 2 = 2 + 1
3 × 4 = 4 × 3
Unsur identitas: operasi perkalian serta penjumlahan setiap bilangan bulat dengan identitasnya dapat menghasilkan bilangan itu sendiri
- Identitas Penjumlahan (0), 7 + 0 = 7
- Identitas Perkalian (1), 2 × 1 = 2
Memiliki Invers: masing-masing bilangan bulat memiliki invers pada operasi penjumlahan, sebuah bilangan bulat yang dioperasikan dengan inversnya akan menghasilkan unsur identitas penjumlahan.
Sebagai contoh:
-7 + 7 = 0; 0 merupakan unsur identitas penjumlahan, sehingga 7 invers penjumlahannya -7
Sifat Distributif: merupakan suatu penggabungan dengan cara mencampur atau mengkombinasikan bilangan dari hasil operasi kepada elemen-elemen kombinasi tersebut.
Mengurutkan Bilangan Bulat
Mengurutkan beberapa bilangan bulat merupakan menuliskan bilangan bulat tersebut secara urut mulai dari dengan nilai yang terbesar atau yang terkecil.
Dalam garis bilangan, semakin ke kanan letak dari sebuah bilangan, maka nilainya akan semakin besar. Sebaliknya, apabila letak dari suatu bilangan semakin ke kiri, maka nilainya akan semakin kecil.
Membandingkan Bilangan Bulat
Berikut adalah beberapa lambang untuk membandingkan dua bilangan bulat, diantaranya adalah sebagai berikut:
- a lebih dari b, ditulis menjadi a > b
- a kurang dari b, ditulis menjadi a < b
- a lebih dari atau sama dengan b, ditulis menjadi a ≥ b
- a kurang dari atau sama dengan b, ditulis menjadi a ≤ b
Bilangan positif selalu memiliki nilai lebih besar dari bilangan negatif
Lawan (Invers) Suatu Bilangan Bulat
Lawan bilangan a merupakan –a. Sebaliknya, lawan –a merupakan a.
Sebagai contoh:
- lawan 5 memiliki nilai lawan –5
- Invers dari –3 memiliki nilai lawan 3
Contoh Soal dan Pembahasan Bilangan Bulat
Soal 1.
Apakah kumpulan dari bilangan berikut ini merupakan bilangan cacah?
2387936, -5673829, 2387844, -273829
Kemudian, urutkan bilangan tersebut dari nilai yang terkecil hingga ke terbesar!
Jawab:
Kumpulan bilangan dari soal di atas bukan merupakan bilangan cacah sebab bilangan tersebut mengandung bilangan bulat negatif (-5673829, -273829) sertan tidak mengandung bilangan nol.
Bilangan bulat positif selalu memiliki nilai lebih besar dari bilangan bulat negatif, maka dari itu:
2387936 > -5673829
2387936 > -273829
2387844 > -5673829
2387844 > -27829
Sekarang, hanya butuh untuk menentukan mana yang lebih kecil di antara 2387936 serta 2387844
Jumlah digit bilangannya sama serta 4 bilangan awal sama, tetapi terdapat perbedaan di bilangan ke-5 2387(9)36, 2387(8)44. Sebab 9 > 8 sehingga 2387936 > 2387844
-5673829 dan -273829
Sebab terdapat perbedaan jumlah digit, yakni -5673829 berjumlah 7 digit dan -273829 berjumlah 6 digit maka dari itu -5673829 berada lebih di kiri dari -273829 pada garis bilangan, sehingga -5673829 < -273829.
Sehingga, bisa kita simpulkan bahwa -5673829 < -273829 < 2387844 < 2387936 dan urutan bilangan dari nilai yang terkecil yaitu -5673829, -273829, 2387844, 2387936.
Soal 2.
Penjumlahan.
1). 4a + 5a = 9a
2). 8z + 4z = 12z
Soal 3. Pengurangan.
1).4a – 5a = -1a
2).8z – 4z = 4z
Soal 4. Penjumlahan dan Pengurangan.
1).10a + 3b + 2a – 7b =
= (10a + 2a) + (3b – 7b)
= 12a – 10b
Soal 5. Perkalian.
(+) x (+) = + contoh: 2 x 5 = 10
(+) x (-) = – contoh: 3 x (-1) = -3
(-) x (+) = – contoh: (-9) x 2 = -16
(-) x (-) = + contoh: (-2) x (-7) = 14
Soal 6. Pembagian.
(+) : (+) = + contoh: 20 : 2 = 10
(+) : (-) = – contoh: 30 : (-5) = -6
(-) : (+) = – contoh: (-10) : 5 = -2
(-) : (-) = + contoh: (-4) : (-1) = 4
Info matematika mengenai Bilangan
Pada Museum Ashmoleandi Oxford yang terletak di Inggris disana terdapat sebuah tongkat kebesaran dari Raja Mesir.
Di mana pada waktu itu yang dalamnya terdapat suatu catatan mengenai 120.000 tawanan perang sekaligus harta rampasan perang yang terdiri atas 400.000 lembu jantan serta 1.422.000 kambing.
Catatan yang diperkirakan sudah ditulis di tahun 3.400 SM ini menunjukkan bukti bahwa pada zaman prasejarah dahulu, manusia sudah belajar menulis mengenai angka-angka dalam sekala besar besar.
Tentu saja, hal tersebut merupakan permulaan penggunaan angka yang sudah jauh sebelum bangsa Mesir memakainya.
Manusia primitif yang hidup dalam gua tentu tidak terlalu membutuhkan banyak hal mengenai matematika atau ilmu berhitung untuk bisa tetao bertahan dalam hidupnya serta melestarikan keturunannya.
Sebab seluruh kebutuhan hidupnya sudah terpenuhi dari alam yang berada di sekitarnya.
Namun, jika seseorang sudah mengumpulkan binatang ternaknya menjadi kawanan ternak atau satu keluarga mulai melakukan hubungan sosial dengan keluarga yang lain, maka mereka butuh untuk memutuskan “berapa yang menjadi milik si A serta berapa yang menjadi milik si B”.
Pada mulanya untuk memenuhi kebutuhan ini, manusia telah merasa cukup jika menggunakan sebuah konsep seperti sedikit, beberapa, atau banyak.
Tetapi lama-kelamaan dibutuhkan untuk mereka agar mempunyai alat ukur yang pasti dalam menentukan “seberapa banyak”.
Nah, dari situlah, orang mulai belajar mengenai cara menghitung dan inilah awal mula dari lahirnya Matematika (Ilmu Hitung).
Demikianlah ulasan singkat mengenai Bilangan Bulat yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.
2 pemikiran pada “Bilangan Bulat”