Barisan dan deret aritmatika dalam ilmu bidang matematika merupakan jenis barisan serta deret bilangan yang di mana bilangan berikutnya adalah penambahan bilangan dari sebelumnya dengan suatu bilangan beda tertentu.
Sebagai contoh 3, 5, 7, 9, 11, 13, ….. Barisan aritmetika ini bisa juga dinyatakan dengan penggunaan rumus sebagai berikut:
a, a + b, a + 2b, a + 3b, …. Informasi selengkapnya mengenai barisan dan deret simak pembahasan berikut ini.
Daftar Isi
Baris Aritmatika
Pengertian Barisan
Barisan merupakan sautu urutan dari suatu anggota-anggota himpunan yang dilandasi dengan suatu aturan tertentu.
Dalam masing-masing angota himpunannya akan diurutkan pada urutan atau suku pertama, kedua, dan seterusnya.
Untuk menyatakan suatu urutan atau suku ke-n dari suatu barisan bisa kita notasikan dengan lambang: Un .
Barisan juga dapat diartikan sebagai fungsi dari bilangan asli atau fungsi yang domainnya merupakan himpunan bilangan asli. Sehingga, Un = f(n)
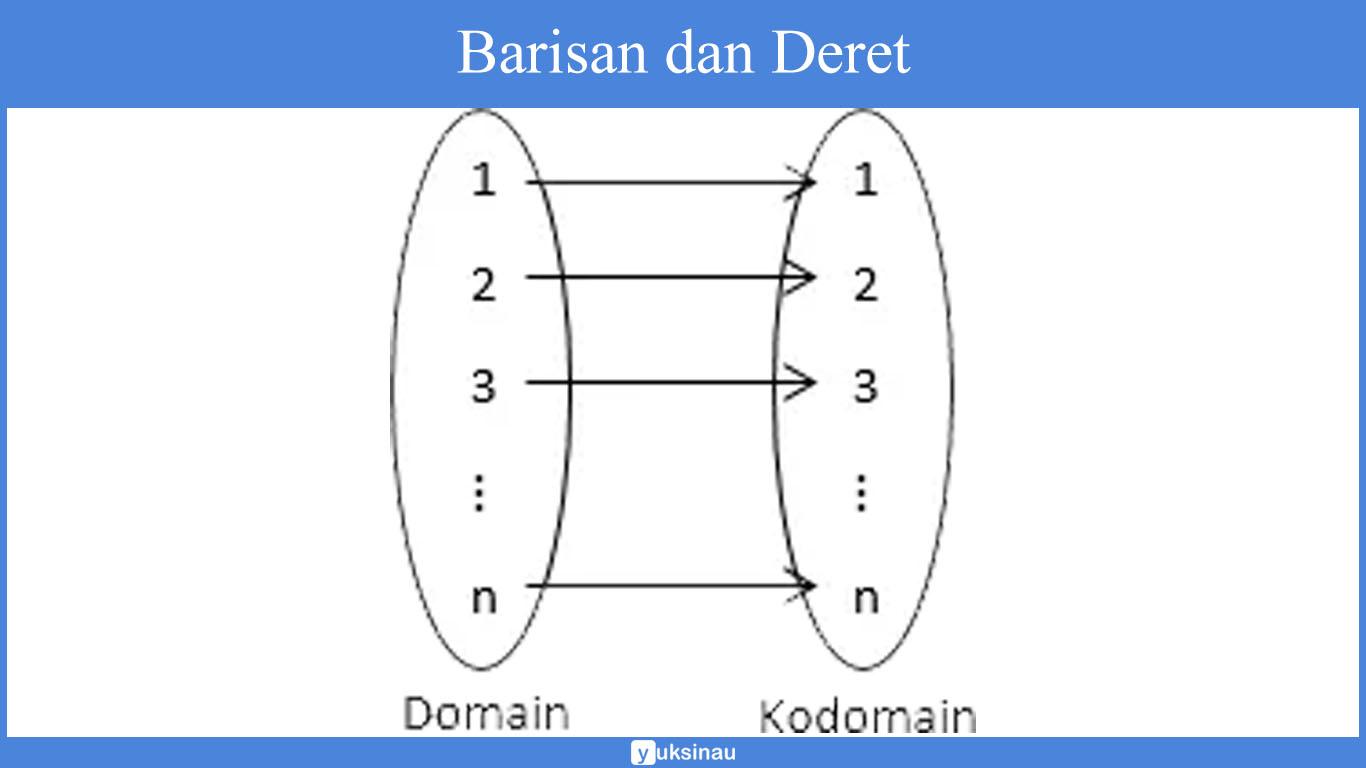
Contoh persoalan:
Misalnya: Un = (2n + 1), maka suku ke-4 dari baris tersebut adalah U4 = (2(4) + 1) = 9.
Barisan merupakan himpunan yang anggotanya adalah hasil pemetaan dari bilangan asli.
Contoh barisan ialah sebagai berikut:
- 1, 2, 3, 4, 5, 6, 7, 8, 9
- 2, 5, 8, 11, 14, 17
- 13, 11, 9, 7, 5, 3
- 1, 1, 2, 3, 5, 8, 13
- 2, 4, 8, 16, 32, 64
Pengertian Baris Aritmatika
Baris aritmatika merupakan suatu baris di mana nilai pada masing-masing sukunya diperoleh dari suku sebelumnya lewat penjumlahan atau pengurangan dengan suatu bilangan b.
Selisih antara nilai suku-suku yang berdekatan tersebut selalu sama yakni b.
Maka:
Un – U(n-1) = b
Sebagai contoh baris 1, 3, 5, 7, 9, merupakan baris aritmatika dengan nilai:
b = (9 – 7) = (7 – 5) = (5 – 3) = (3 – 1) = 2
Untuk mengetahui nilai suku ke-n dari sebuah barisan aritmatika, bisa kita ketahui dengan cara mengetahui nilai suku ke-k dan selisih antar suku yang berdekatan (b).
Adapaun rumusnya seperti yang tertera di bawah ini:
Un = Uk + (n – k)b
Jika yang diketahui merupakan nilai suku pertama Uk = a serta selisih antar sukunya (b), maka nilai k = 1 dan juga nilai Un = adalah
Un = a + (n – 1)b
Suku Tengah Barisan Aritmatika
Apabila terdapat barisan aritmatika yang memiliki banyak suku (n) ganjil, suku pertama a, dan juga suku terakhir Un maka suku tengah Ut dari barisan tersebut ialah sebagai berikut.
Ut = 1/2(a + Un)
dengan t = 1/2(n+1)
Rumus Suku ke-n Barisan Aritmatika
Un = a + (n – 1)b
Keterangan:
Un= suku ke-n
a= suku pertama
b= beda
n= banyak suku
Sisipan pada Barisan Aritmatika
Apabila diantara dua suku barisan aritmatika disisipkan k buah suku sehingga akan terbentuk barisan aritmatika baru. Maka perbedaab barisan aritmatika sesudah disisipkan k buah suku akan berubah.
Beda dari barisan aritmatika ini sesudah disisipkan k buah suku ialah sebagai berikut.
b’ = b/(k + 1)
Keterangan:
b’= beda barisan aritmatika sesudah disisipkan k buah suku
k= banyak suku yang disisipkan
Banyak suku dari barisan aritmatika yang disisipkan k buah suku juga akan mengalami perubahan, menjadi seperti berikut.
n’ = n + (n – 1)k
Keterangan:
n’= merupakan banyak suku barisan aritmatika baru.
n= merupakan banyak suku barisan aritmatika lama.
Deret Aritmatika
Pengertian Deret
Deret merupakan suatu penjumlahan dari anggota-anggota sebuah barisan.
Contoh deret:
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
- 2 + 5 + 8 + 11 + 14 + 17
- 13 + 11 + 9 + 7 + 5 + 3
Pengertian Deret Aritmatika
Deret aritmatika merupakan suatu penjumlahan antar suku-suku dari sebuah barisan aritmatika. Penjumlahan dari suku-suku petama hingga suku ke-n barisan aritmatika tersebut bisa dihitung sebagai:
Sn = U1 + U2 + U3 + …. + U(n-1)
atau sebagai =
Sn = a + (a + b) + (a + 2b) + …. + (a + (n – 2)b) + (a + (n – 1)b)
Jika, hanya diketahui nilai a merupakan suku pertama serta nilainya merupakan suku ke-n, maka nilai deret aritmatikanya yakni:
Sn = n/2(a + Un)
Persamaan tersebut bisa kita balim untuk mencari nilai suku ke-n menjadi:
Sn = U1 + U2 + U3 + …. + U(n-1)
S(n-1) = U1 + U2 + U3 + …. + U(n-1)
Sn – S(n-1) = Un
Sehingga akan kita dapatkan rumus akhir sebagai berikut:
Un = Sn – S(n-1)
Deret aritmatika merupakan suatu jumlah dari suku-suku barisan aritmatika. Deret aritmatika untuk n suku pertama dinotasikan dengan huruf Sn serta mempunyai rumus sebagai berikut.
Sn = n/2(a + un)
ataupun
Sn = n/2(2a + (n – 1)b)
Keterangan:
Sn= jumlah n suku pertama
a= suku pertama
Un= suku ke-n atau suku terakhir
b= beda
n= banyak suku
Geometri
Barisan geometri merupakan suatu barisan dengan pembanding antara dua suku berurutan yang selalu bersifat tetap.
Pembanding dari dua suku berurutan tersebut dinamakan sebagai rasio, yang biasa dinotasikan dengan penggunaan huruf r.
Adapun rumus umum untuk rasio pada geometri, yaitu:
![]()
Rumus Suku ke-n pada Barisan Geometri
Un = arn – 1
Keterangan:
Un merupakan suku ke-n.
a merupakan suku pertama.
r merupakan rasio.
n merupakan banyak suku.
Suku Tengah Barisan Geometri
Apabila suatu barisan geometri memiliki banyak suku (n) ganjil, suku pertama a, serta suku terakhir Un maka suku tengah Ut dari barisan tersebut ialah sebagai berikut.
Rumus suku tengah barisan geometri:
![]()
Sisipan pada Barisan Geometri
Apabila diantara dua suku barisan geometri disisipkan k buah suku sehingga akan terbentuk barisan geometri baru sehingga rasio barisan geometri sesudah disisipkan k buah suku akan mengalami perubahan.
Rasio dari barisan geometri sesudah disisipkan k buah suku ialah seperti berikut ini:
![]()
Keterangan:
r’ merupakan rasio barisan geometri setelah disisipkan k buah suku.
k merupakan banyak suku yang disisipkan.
Banyak suku dari barisan geometri yang disisipkan k buah suku juga akan mengalami perubahan, menjadi seperti yang ada di bawah ini:
n’ = n + (n – 1)k
Keterangan:
n’ merupakan banyak suku barisan geometri baru.
n merupakan banyak suku barisan geometri lama.
Deret Geometri
Deret geometri merupakan jumlah dari suku-suku barisan geometri. Deret geometri bagi n suku pertama dinotasikan dengan penggunaan huruf Sn serta mempuyai rumus seperti berikut ini:
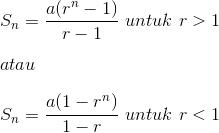
Keterangan:
Sn merupakan jumlah n suku pertama.
a merupakan suku pertama.
r merupakan rasio.
n merupakan banyak suku.
Deret Geometri Tak Berhingga
Barisan geometri dengan rasio antara -1 serta 1 disebut sebagai barisan geometri yang konvergen.
Deret geometri dari barisan geometri yang konvergen serta banyak suku tak berhingga bisa kita hitung dengan menggunakan rumus yang ada di bawah ini:
![]()
Keterangan:
a merupakan suku pertama.
r merupakan rasio dengan syarat -1< r <1.
Hubungan Barisan dan Deret
- Un = Sn – Sn – 1
- Beda barisan aritmatika bisa kita dapatkan dari turunan kedua deret aritmatika.
Contoh Soal dan Pembahasan Barisan dan Deret
Barisan dan Deret Aritmatika
Soal 1. Barisan dan Deret Aritmatika
Suatu barisan aritmatika mempunyai jumlah suku ganjil. Apabila suku pertamanyanya 4 atau suku terakhirnya yaitu 20, maka dari suku tengahnya adalah …
a. 12
b. 8
c. 10
d. 16
Jawab:
a = 4
Un = 20
Ut= a + Un2 = 20 + 42= 12
Jawaban: a
Soal 2. Barisan dan Deret Aritmatika
Diketahui suatu barisan aritmatika sebanyak tujuh suku. Apabila suku pertama serta nilai bedanya ialah 2. Hitunglah suku tengahnya ?
a. 9
b. 8
c. 10
d. 12
Jawab:
a = 2
b = 2
n = 7
Ut= a + (n-1)b2 Ut= a + (n-1)b2 = 2 + (7-1)22 = 8
Soal 3. Barisan dan Deret Aritmatika
Suku ke-15 dari barisan: 2, 5, 8, 11, 14, … ialah…
a.41
b.44
c.45
d.47
Jawab:
Barisan di atas adalah sebuah barisan aritmatika sebab juga mempunyai beda yang sangat konstan.
- Suku pertama adalah = a= U1= 2
- Beda adalah = b =U2 – U1= 5–2 adalah 3
Suku ke-15 = U15
Un = a + (n – 1) b
U15 = 2 + (15 – 1) 3
= 2 + 14 . 3
= 2 + 42
= 44
Soal 5. Barisan dan Deret Aritmatika
Suku ke-45 dari barisan bilangan: 3, 7, 11, 15, 19, … adalah…
a.-179
b.-173
c.173
d.179
Jawab:
Barisan di atas adalah suatu barisan aritmatika, sebab juga banyak mempunyai beda yang sama.
- Suku pertama = a = 3
- Beda = b = U2 – U1 = 7–3 adalah 4
Un = a + (n – 1) b
U45 = 3 + (45 – 1) 4
= 3 + 44 . 4
= 3 + 176
= 179
Soal 6. Barisan dan Deret Aritmatika
Suku ke-50 dari barisan bilangan: 20, 17, 14, 11, 8, … ialah…
a.-167
b.-127
c.127
d.167
Jawab:
Barisan di atas adalah sebuah barisan aritmatika, sebab juga banyak mempunyai beda yang sama.
- Suku pertama adalah = a = 20
- Beda adalah = b = U2 – U1 = 17 – 20 adalah -3
Un = a + (n – 1) b
U50 = 20 + (50 – 1) -3
= 20 + 49 . (-3)
= 20 + (-147)
= -127
Soal 7. Barisan dan Deret Aritmatika
Rumus suku ke-n barisan aritmatika 94, 90, 86, 82, … ialah…
a.Un = 90 + 4n
b.Un = 94 + 4n
c.Un = 94 – 4n
d.Un = 98 – 4n
Jawab:
- Suku pertama adalah = a = 94
- Beda adalah = b = 90 – 94 adalah -4
suku ke-n merupakan:
Un = a +(n-1) b
= 94 + (n-1) -4
= 94 + (-4n) + 4
= 94 + 4 – 4n
= 98 – 4n
Soal 8. Barisan dan Deret Aritmatika
Diketahui juga deret aritmatika 17, 20, 23, 26, … Jumlah 30 suku pertama deret tersebut adalah…
a. 1.815
b. 2.520
c. 2.310
d. 2.550
Jawab:
- suku pertama adalah = a = 17
- Beda adalah = b = U2-U1 = 20-17 adalah 3
- Jumlah 30 suku pertama adalah = S30
Sn = n/2 (2a + (n-1)b)
S30 = 30/2 (2.17 + (30-1)3)
= 15 (34 + 29.3)
= 15 (34 + 87)
= 15.121
= 1.815
Soal 9.
Diketahui deret aritmatika dengan rumus Sn = 2n^2 + 3n. Beda deret aritmatika tersebut yaitu…
a. 3
b. 4
c. 5
d. 9
Jawab:
Beda bisa kita cari dengan cara mengurangkan jumlah 2 suku (S2) dengan jumlah 1 suku (S1), sehingga:
Sn = 2n^2 + 3n
S2 = 2.2^2 + 3.2
= 2.4 + 6
= 8 + 6
= 14
Sn = 2n^2 + 3n
S1 = 2.1^2 + 3.1
= 2.1 + 3
= 2 + 3
= 5
beda = b = S2-S1
= 14 – 5
= 9
Soal 10.
Diketahui sebuah barisan aritmatika. Suku pertama barisan tersebut ialah 25 atau suku kesebelas ialah 55.
Suku ke-45 barisan tersebut yaitu…
a. 157
b. 163
c. 169
d. 179
Jawab:
U1 = a = 25
U11 = 55
a + (11-1)b = 55
25 + 10b = 55
10b = 55-25
10b = 30
b = 30/10
b = 3
Kemudian, kita diminta untuk mencari U-45, sehingga:
Un = a + (n-1)b
U45 = 25 + (45-1)3
= 25 + 44.3
= 25 + 132
= 157
Jawaban: a.
Barisan dan Deret Geometri
Soal 1. Barisan dan Deret Geometri
Diketahui suatu barisan geometri di mana untuk mencari suku Un.
Tentukanlah suku Un yang ke 10 dari barisan 1/8, 1/4, 1/2,…. tersebut!
Jawab:
Diketahui:
- = r = 1/4 : 1/8 = 1/4 x 8 = 2 (rasionya)
- a = 1/8
Penyelesaian:
- Un = arn – 1
- Un = 1/8 . 2 (10 – 1) = 1/8 . 29 = 2 – 3 . 29 = 26 = 64
Sehingga, suku Un yang ke 10 tersebut yaitu = 64
Soal 2.
Diketahui sebuah amoeba membelah diri menjadi 2 setiap 6 menit, berapakah jumlah amoeba sesudah satu jam apabila awalnya hanya terdapat 2 amoeba.
Hitunglah suku Un jumlah amoeba tersebut!
Jawab:
Diketahui:
- a = 2
- r = 2
- n = (1 jam/6 menit) + 1 = 11
Penyelesaian:
- Un = arn – 1
- Un = 2 . 2 11 – 1 = 210 = 1024 buah amoeba
Sehingga, suku Un untuk mencari amoeba di atas yaitu = 1024 buah amoeba
Soal 3.
Diketahui suatu barisan geometri untuk mencari suku Un.
Tentukan suku Un yang ke 7 dari barisan 3, 6, 2,…. tersebut!
Jawab:
Diketahui:
- a = 3
- r = 2
Penyelesaian:
- Un = ar(n-1)
- Un = 3.2(7-1)
- U7 = 3.2(7-1)
- U7 = 192
Sehingga, suku Un yang ke 17 tersebut yaitu = 192
Soal 4.
Diketahui suatu barisan geometri untuk mencari suku Un.
Tentukan suku Un yang ke 7 dari barisan 48, 24, 12,…. tersebut!
Jawab:
Diketahui:
- a = 48
- r = 1/2
Penyelesaian:
- Un = arn-1
- Un = 48.(1/2)n-1
- Un = 48.(1/2)n-1
- Un = 48.(2-1)1-n
- Un = 3.16. (2)1-n
- U7 = 3.24 (2)1-n
- U7 = 3.25-n
Sehingga, suku Un yang ke 7 tersebut yaitu = 3.25-n
Soal 5.
Terdapat sutau barisan geometri untuk mencari suku Un.
Hitunglah suku Un yang ke 7 dari barisan 44, 24, 12,…. tersebut!
Jawab:
Diketahui:
- a = 44
- r = 1/2
Penyeleasaian:
- Un = arn-1
- Un = 44.(1/2)n-1
- Un = 44.(1/2)n-1
- Un = 44.(2-1)1-n
- Un = 3.8. (2)1-n
- U7 = 3.23 (2)1-n
- U7 = 3.24-n
Sehingga, suku Un yang ke 7 tersebut yaitu = 3.24-n
Soal 6.
Diketahui suatu barisan geometri untuk mencari suku Un.
Carilah suku Un yang ke 7 dari barisan 42, 24, 12,…. tersebut!
Jawab:
Diketahui:
- a = 42
- r = 1/2
Penyelesaian:
- Un = arn-1
- Un = 42.(1/2)n-1
- Un = 42.(1/2)n-1
- Un = 42.(2-1)1-n
- Un = 3.4. (2)1-n
- U7 = 3.22 (2)1-n
- U7 = 3.23-n
Sehingga, suku Un yang ke 7 tersebut yaitu = 3.23-n
Soal 7.
Diketahui suatu barisan geometri untuk mencari suku Un.
Carilah suku Un yang ke 7 dari barisan 58, 24, 12,…. tersebut!
Jawab:
Diketahui:
- a = 48
- r = 1/2
Penyelesaian:
- Un = arn-1
- Un = 58.(1/2)n-1
- Un = 58.(1/2)n-1
- Un = 58.(2-1)1-n
- Un = 4.16. (2)1-n
- U7 = 4.24 (2)1-n
- U7 = 4.25-n
Sehingga, suku Un yang ke 7 tersebut yaitu = 4.25-n
Soal 8.
Dalam sebuah deret geometri diketahui U1 = 6 dan U5 = 486. Berapakah besar rasionya ?
Jawab:
U1 = 6
U5 = 486
n = 5
Un = U1 × rn-1
U5 = 6 × r5-1
486 = 6 × r4
r4 = 486/6
= 81
r = ± ![]()
r = 3 atau -3
Sehingga rasio deret tersebut adalah 3 atau -3.
Soal 9.
Dalam sebuah deret geometri diketahui U3 = 81 dan U6 = 3. Maka hitunglah deret tersebut!
Jawab:
U3 = 81, maka U1 × r² = 81
U6 = 3, maka U1 × r5 = 3
U6/U3 = ( U1 × r5 )/( U1 × r² ) = 3/81
r³ = 1/27
r = akar pangkat 3 dari (1/27)
r = 1/3
U1 × r² = 81
U1 × (1/3)² = 81
U1 × 1/9 = 81
U1 = 81 : 1/9
U1 = 81 × 9
U1 = 729
Sehingga deret tersebut yaitu 729+243+81+27+…
Soal 10.
Suku pertama dari sebuah deret geometri adalah 2 serta rasionya adalah 3. Apabila suku tengah deret tersebut adalah 54, maka tentukanlah:
a. suku terakhir dari deret tersebut.
b. banyak suku pada deret tersebut.
Jawab:
a. U1 = 2
Ut = 54
r = 3
Ut = √(U1×Un)
54 = √(2×Un)
54² = 2×Un
2.916 = 2Un
Un = 2.916/2
Un = 1.458
Sehingga, suku terakhir (Un) dari deret tersebut adalah 1.458.
b. Un = U1 × rn-1
1.458 = 2 × (3)n-1
(3)n-1 = 1.458/2
(3)n-1 = 729
(3)n-1 = 36
n-1 = 6
n = 7
Sehingga, banyak suku pada deret tersebut ialah 7.
Demikianlah ulasan singkat terkait Barisan dan Deret yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.